Как рассчитать угловой размер солнца
Работа N 7. Определение угловых и линейных размеров Солнца (или Луны)
I. С помощью теодолита.
1. Установив прибор и вставив светофильтр в окуляр трубы, совместить нуль алидады с нулем горизонтального лимба. Закрепить алидаду и при открепленном лимбе навести трубу на Солнце так, чтобы вертикальная нить касалась правого края диска Солнца (это достигается с помощью микрометрического винта лимба). Затем быстрым вращением микрометрического винта алидады перевести вертикальную нить на левый край изображения Солнца. Сняв показания с горизонтального лимба, и получают угловой диаметр Солнца.
2. Вычислить радиус Солнца по формуле:
R = D ∙ sin r
где r — угловой радиус Солнца, D — расстояние до Солнца.
3. Для вычисления линейных размеров Солнца можно воспользоваться и другой формулой. Известно, что радиусы Солнца и Земли связаны с расстоянием до Солнца соотношением:
R = D ∙ sin r ,
R0 = D ∙ sin p,
где r — угловой радиус Солнца, а p — его параллакс.
Поделив почленно эти равенства, получим:
Ввиду малости углов, отношение синусов можно заменить отношением аргументов.
Тогда 
Значения параллакса р и радиуса Земли берутся из таблиц.
| R0= 6378 км, |  |
| r = 16′ | |
| p = 8″,8 |
Отношение 
Аналогично определяются и размеры Луны.
II. По времени прохождения диска светила через вертикальную нить оптической трубы
Если смотреть на Солнце (или Луну) в неподвижный телескоп, то вследствие суточного вращения Земли светило будет постоянно уходить из поля зрения телескопа. Для определения углового диаметра Солнца, с помощью секундомера измеряют время прохождения его диска через вертикальную нить окуляра и найденное время умножают на cos d , где d — склонение светила 1 . Затем время переводят в угловые единицы, помня, что за 1 мин Земля поворачивается на 15′, а за 1 сек. — на 15″. Линейный диаметр D определяется из соотношения:

где R — расстояние до светила, a — его угловой диаметр, выраженный в градусах.
Если использовать угловой диаметр, выраженный в единицах времени (например, в секундах), то
где t — время прохождения диска через вертикальную нить, выраженное в секундах.
Дата наблюдения — 28 октября 1959 г.
Время прохождения диска через нить окуляра t = 131 сек.
Склонение Солнца на 28 октября d = — 13њ.
Угловой диаметр Солнца a = 131∙ cos 13њ = 131∙0,9744 = 128 сек. или в угловых единицах a = 32 = 0,533њ.
| Линейный диаметр Солнца |  |
1. Из двух способов второй более доступен. Он проще по технике выполнения и не требует какой-либо предварительной тренировки.
2. Проводя такие измерения, интересно отметить разницу в величине видимого диаметра Солнца, когда оно бывает в перигее и апогее. Разница эта составляет около 1′ или по времени — 4 сек.
В значительно больших пределах изменяется видимый диаметр Луны (от 33′,4 до 29′,4). Это хорошо видно из рис. 55. Здесь уже разница во времени — около 16 сек.

Рис. 55. Наибольший и наименьший видимые размеры диска Луны, расположенные концентрически (слева) эксцентрически (справа).
Такие наблюдения будут воочию убеждать учащихся в том, что орбиты Земли и Луны не круговые, а эллиптические (иллюстрация к законам Кеплера).
3. Пользуясь вторым способом, можно определять размеры некоторых лунных образований, длину теней от гор и др.
Источник
Угловой размер, линейный размер и расстояние
Калькуляторы рассчитвающие параметры по соотношениям между угловым размером тела, линейным размером тела и расстоянием до тела.
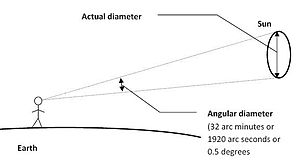
Угловой размер — это угол между линиями, соединяющими диаметрально противоположные точки измеряемого объекта и глаз наблюдателя.
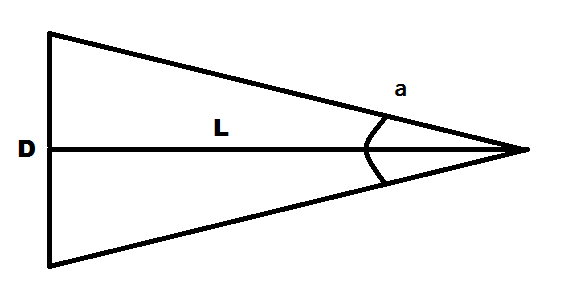
Посмотрим на рисунок: здесь отрезок D — измеряемый объект, отрезок L — линия наблюдения, перпендикулярная отрезку D и являющаяся его серединным перпендикуляром, и угол а — угловой размер отрезка D.
Очевидные соотношения между величинами (вспомним тригонометрию):
Таким образом, наблюдатель, зная, например, линейный размер объекта, по угловому размеру объекта может определить расстояние до него. Помню, раньше для этих целей военные бинокли снабжали специальными риcками для определения углового размера.
Ну и обратные задачи тоже имеют место — зная, например, расстояние и линейный размер объекта, можно определить его угловой размер; и наконец, зная расстояние и угловой размер, можно определить линейный размер. Последние задачи актуальны для астрономии. Там используют термин угловой диаметр — то есть видимый диаметр небесного тела, выраженный в угловых мерах.
Ниже калькуляторы, рассчитывающие неизвестные по всем соотношениям. В качестве данных по умолчанию используется расстояние от Земли до Солнца, диаметр Солнца и средний угловой диаметр Солнца, наблюдаемого с Земли.
Источник
Угловой диаметр — Angular diameter
Угловой диаметр , угловой размер , видимый диаметр , или видимого размер является угловым расстоянием , описывающим , как большой шар или круг появляется из данной точки зрения. В науках о зрении это называется углом обзора , а в оптике — угловой апертурой ( линзы ). В качестве альтернативы угловой диаметр можно рассматривать как угловое смещение, на которое глаз или камера должны повернуться, чтобы смотреть с одной стороны видимого круга на противоположную. Угловой радиус равен половине углового диаметра.
СОДЕРЖАНИЕ
Формула
Угловой диаметр круга , плоскость которого перпендикулярна вектору смещения между точкой обзора и центром указанного круга, может быть вычислен по формуле
δ знак равно 2 арктан ( d 2 D ) , <\ displaystyle \ delta = 2 \ arctan \ left (<\ frac
где — угловой диаметр, — фактический диаметр объекта и — расстояние до объекта. Когда имеем , а полученный результат выражается в радианах . δ <\ displaystyle \ delta> 



Для сферического объекта, фактический диаметр которого равен, а где — расстояние до центра сферы, угловой диаметр можно найти по формуле d а c т , <\ displaystyle d _ <\ mathrm 
δ знак равно 2 Arcsin ( d а c т 2 D ) <\ displaystyle \ delta = 2 \ arcsin \ left (<\ frac
Разница связана с тем, что видимые края сферы — это точки ее касания, которые находятся ближе к наблюдателю, чем центр сферы. Разница существенна только для сферических объектов большого углового диаметра, поскольку для малых значений справедливы следующие малоугловые приближения : Икс <\ displaystyle x>
Arcsin Икс ≈ арктан Икс ≈ Икс <\ Displaystyle \ arcsin x \ приблизительно \ arctan x \ приблизительно x> 
Оценка углового диаметра с помощью руки
Оценки углового диаметра можно получить, держа руку под прямым углом к полностью вытянутой руке , как показано на рисунке.
Использование в астрономии
В астрономии размеры небесных объектов часто указываются в терминах их углового диаметра, видимого с Земли , а не их реальных размеров. Поскольку эти угловые диаметры обычно малы, их принято представлять в угловых секундах (″). Угловая секунда равна 1/3600 части одного градуса (1 °), а радиан — 180 градусов. Таким образом, один радиан равен 3600 × 180 / угловую секунду, что составляет примерно 206 265 угловых секунд (1 рад ≈ 206 264,806247 дюймов). Следовательно, угловой диаметр объекта с физическим диаметром d на расстоянии D , выраженный в угловых секундах, определяется следующим образом: π <\ displaystyle \ pi> 
δ знак равно 206 , 265 ( d / D ) а р c s е c о п d s <\ displaystyle \ delta = 206 265
\ mathrm 
Эти объекты имеют угловой диаметр 1 дюйм:
- объект диаметром 1 см на удалении 2,06 км
- объект диаметром 725,27 км на расстоянии 1 астрономической единицы (а.е.)
- объект диаметром 45 866 916 км на расстоянии 1 светового года
- объект диаметром 1 а.е. (149 597 871 км) на расстоянии 1 парсек (пк)
Таким образом, угловой диаметр орбиты Земли вокруг Солнца, если смотреть с расстояния 1 пк, составляет 2 дюйма , поскольку 1 а.е. — это средний радиус орбиты Земли.
Угловой диаметр Солнца с расстояния в один световой год составляет 0,03 дюйма , а Земли — 0,0003 дюйма. Угловой диаметр Солнца 0,03 дюйма, указанный выше, примерно такой же, как у человеческого тела на расстоянии диаметра Земли.
В этой таблице показаны угловые размеры примечательных небесных тел с Земли:
| Небесное тело | Угловой диаметр или размер | Относительный размер |
|---|---|---|
| Галактика Андромеды | 3 ° 10 ′ на 1 ° | Примерно в шесть раз больше Солнца или Луны. Без фотографии с длинной выдержкой видно только гораздо меньшее ядро . |
| солнце | 31′27 ″ — 32′32 ″ | 30–31 раз больше максимального значения для Венеры (оранжевая полоса внизу) / 1887–1952 ″ |
| Луна | 29′20 ″ — 34′6 ″ | 28–32,5 раза больше максимального значения для Венеры (оранжевая полоса внизу) / 1760–2046 ″ |
| Туманность Спираль | примерно 16 ‘на 28’ | |
| Шпиль в туманности Орла | 4′40 ″ | длина 280 ″ |
| Венера | 9,7 ″ — 1′6 ″ | |
| Юпитер | 29,8 ″ — 50,1 ″ | |
| Сатурн | 14,5–20,1 дюйма | |
| Марс | 3,5–25,1 дюйма | |
| Меркурий | 4,5–13,0 дюймов | |
| Уран | 3,3 дюйма — 4,1 дюйма | |
| Нептун | 2,2 ″ — 2,4 ″ | |
| Церера | 0,33–0,84 дюйма | |
| Веста | 0,20–0,64 дюйма | |
| Плутон | 0,06–0,11 дюйма | |
| Р Дорадус | 0,052 ″ — 0,062 ″ | |
| Бетельгейзе | 0,049 ″ — 0,060 ″ | |
| Эрис | 0,034 ″ — 0,089 ″ | |
| Alphard | 0,00909 ″ | |
| Альфа Центавра A | 0,007 ″ | |
| Канопус | 0,006 ″ | |
| Сириус | 0,005936 ″ | |
| Альтаир | 0,003 ″ | |
| Денеб | 0,002 ″ | |
| Проксима Центавра | 0,001 ″ | |
| Альнитак | 0,0005 ″ | |
| Горизонт событий черной дыры M87 * в центре галактики M87, полученный телескопом Event Horizon в 2019 году. | 0,000025 ″ | |
| Звезда, подобная Альнитак, на таком расстоянии, где космический телескоп Хаббла мог бы ее просто увидеть | 6 × 10 −10 угловых секунд |
Таблица показывает, что угловой диаметр Солнца, если смотреть с Земли, составляет приблизительно 32 ‘(1920 ″ или 0,53 °), как показано выше.
Таким образом, угловой диаметр Солнца примерно в 250 000 раз больше диаметра Сириуса . (Сириус имеет в два раза диаметр и расстояние 500000 раза больше , чем; Солнце 10 10 раз ярче, соответствующий угловой диаметру 10 5 , так что Сириус примерно 6 раз ярче на единицу телесного угла ) .
Угловой диаметр Солнца также примерно в 250 000 раз больше, чем у Альфы Центавра A (у него примерно такой же диаметр, а расстояние в 250 000 раз больше; Солнце в 4 × 10 10 раз ярче, что соответствует соотношению угловых диаметров 200000, поэтому Alpha Centauri A немного ярче на единицу телесного угла).
Угловой диаметр Солнца примерно такой же, как у Луны . (Диаметр Солнца в 400 раз больше, равно как и расстояние до него; Солнце в 200000-500000 раз ярче полной Луны (цифры различаются), что соответствует отношению углового диаметра от 450 до 700, то есть небесное тело с диаметром 2,5–4 ″ и такой же яркости на единицу телесного угла будет иметь такую же яркость, как полная Луна.)
Хотя Плутон физически больше Цереры, если смотреть с Земли (например, через космический телескоп Хаббл ), Церера имеет гораздо больший видимый размер.
Угловые размеры, измеряемые в градусах, полезны для больших участков неба. (Например, три звезды Пояса имеют угловой размер около 4,5 °.) Однако для измерения угловых размеров галактик, туманностей или других объектов ночного неба требуются гораздо более точные единицы .
Таким образом, степени подразделяются следующим образом:
- 360 градусов (°) по полному кругу
- 60 угловых минут (‘) на один градус
- 60 угловых секунд (″) в одной угловой минуте
Чтобы представить это в перспективе, полная Луна, если смотреть с Земли, составляет около 1 ⁄ 2 °, или 30 футов (или 1800 ″). Движение Луны по небу можно измерить по угловому размеру: примерно 15 ° каждый час или 15 дюймов в секунду. Линия длиной в одну милю, нарисованная на лице Луны, будет казаться с Земли примерно 1 дюйм в длину.
В астрономии обычно трудно напрямую измерить расстояние до объекта, но объект может иметь известный физический размер (возможно, он похож на более близкий объект с известным расстоянием) и измеримый угловой диаметр. В этом случае формулу углового диаметра можно инвертировать, чтобы получить расстояние по угловому диаметру до удаленных объектов как
d ≡ 2 D загар ( δ 2 ) <\ Displaystyle д \ эквив 2D \ загар \ влево (<\ гидроразрыва <\ дельта><2>> \ вправо)> 
В неевклидовом пространстве, таком как наша расширяющаяся Вселенная, расстояние по угловому диаметру является лишь одним из нескольких определений расстояния, так что могут быть разные «расстояния» до одного и того же объекта. См. Меры расстояния (космология) .
Некруглые объекты
Многие объекты дальнего космоса, такие как галактики и туманности, кажутся некруглыми, и поэтому обычно имеют две меры диаметра: большую ось и малую ось. Например, Малое Магелланово Облако имеет видимый диаметр 5 ° 20 ′ × 3 ° 5 ′.
Дефект освещения
Дефект освещения — это максимальная угловая ширина неосвещенной части небесного тела, видимой данным наблюдателем. Например, если объект имеет диаметр 40 дюймов в диаметре и освещен на 75%, дефект освещения составляет 10 дюймов.
Источник