Масса Солнца

Очень часто ученики не могут понять, как определили массы планет и Солнца. При этом они соглашаются с тем, что расстояния до того или иного объекта можно измерить, можно измерить и линейные размеры, но вычислить массу космических тел считают невозможным. «Их, что на весах взвешивали, что ли?» — такой вопрос приходится очень часто слышать. Так как же, происходит «взвешивание» космических объектов? Оказывается, не так уж и сложно. Ученик средней школы может сам найти массу того же Солнца.

Вот ка это делается.

Известно, что Земля вращается вокруг Солнца по орбите с радиусом около 150 млн. км. период обращения составляет 1 год, или 365 суток = 365х24х3600 секунд, что примерно составляет: 31,5 млн. секунд.

Земля на орбите удерживается благодаря гравитационным силам по закону тяготения:

Так как Земля движется по окружности, следовательно, с центростремительным ускорением. Если наша планета движется с ускорением, значит, на нее действует сила по II закону Ньютона.

Это та самая сила, с которой Солнце и наша планета взаимодействуют, т.е. сила гравитации о котрой говорилось выше. Если это одна и та же сила, то мы можем приравнять правые части уравнений:

Делим обе части на массу земли

Отсюда можно выразить массу Солнца:

Найдем теперь центростремительное ускорение , где скорость определяется как равномерная. Напомню, что при равномерном движении по окружности, скорость изменяет только свое направление.

или для движения по окружности

Теперь можно вычислить скорость, а затем ускорение и уже после сможем найти массу Солнца, но мы подставим последние 3 формулы в выражения для определения массы сОлнца и получим:

Произведем подстановку и вычисления, учитывая, что R =150 млн. км В СИ составляет 1,5 • 10 11 м, находим, что масса Солнца составляет примерно 2•10 30 кг.

Вот таким образом, имея только школьные знания в области физики и математики, можно найти массу Солнца.

Источник

Масса Солнца

Ввиду значительной удалённости от планеты Земля Солнце воспринимается человеком как тело, имеющее небольшой размер. По земным оценкам и меркам кажется, что видимый поперечник составляет 50-70 см. Если бы человек имел возможность «приземления» на Плутон, размеры светила показались бы ему другими. Итак, какова масса Солнца на самом деле – ответ на этот вопрос будет рассмотрен в статье.

О действительных размерах

Солнце – значительный по размерным показателям космический объект, который однозначно превосходит Землю в 1,3 млн раз! Значение поперечника светила нашей системы в 109 раз выше, нежели идентичный параметр у Земли, и составляет оно 1,4 млн км.

Чтобы масса Солнца была представлена более наглядно, стоит рассмотреть её в сравнительной картине. В 1 ведро можно вместить 130 тыс. пшеничных зёрен. Если в кучу будет высыпано 10 вёдер, а в сторону – положено одно маленькое зёрнышко, соотношение между этими частями будет иметь соответствие пропорциям, наблюдаемым между нашей звездой и Землёй.

Но масса Солнца с весом Земли имеет несколько другое соотношение: среднее значение плотности небесного светила вчетверо меньше, чем нашей планеты, этот показатель равняется 1,4 величины плотности воды. В свою очередь, масса Солнца превышает идентичный параметр Земли в 300 000 раз. В отношении всех планет Солнечной системы и их спутников это значение больше в 750 раз.

Весовой параметр Земли составляет, если представить точные данные, 5 958 000 000 000 000 000 000 тонн. Если выразить подобным образом вес Солнца, будет получено число, в составе которого – одна двойка и 27 нулей.

Земля и Солнце (фотомонтаж с сохранением соотношения размеров)

Известные научные сведения

Солнечная масса, или, говоря другими словами, масса Солнца, представляет собой единицу измерения массы, имеющую внесистемный тип. Она используется в астрономической науке в целях выражения звёздных весов, а также определения значений в отношении прочих астрономических объектов, к примеру, галактик, солнечных систем. Обозначение, используемое в обиходе учёных и рядовых обывателей – M. В астрономической науке его принято записывать следующим образом: M = 1,98847 * 10^30 кг.

Первый множитель не имеет максимально точного определения, поэтому может обозначаться как «плюс» или «минус» 0,00007 единиц. Массовое значение нашего естественного небесного светила, как известно, выше идентичного показателя Земли в 332 946 раз. А по точным подсчетам учёных 99,86% всей массы, относящейся к Солнечной системе, содержится именно в нашей звезде. Суммарная доля всех остальных планет имеет значение 0,0013M, причём максимальная часть приходится на Юпитер, который Солнце превышает по весу лишь в 1047,56 раз.

Физические характеристики Солнца

Формула определения

Львиная доля отдельных звёзд, присутствующих во Вселенной, имеют массовое значение от 0,08 до 50 единиц, а весовой показатель чёрных дыр и целых галактических пространств может достигать миллионов и миллиардов масс нашего главного яркого объекта. Масса Солнца, согласно формулам, разработанным в астрономической науке, может быть определена на основании формулы, которая следует из третьего закона Кеплера.

Формула расчёты солнечной массы

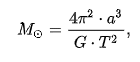
M = (4 * ПИ^2 * a^3) / (G * T^2),
где a – длина, которой обладает большая полуось орбитальной части планеты;
G есть величина гравитации Ньютона, которая является постоянной;
Значение T представляет собой сидерический период, в течение которого планета делает оборот вокруг нашей звезды, для Земли это значение равняется году.

Таким образом, рассматриваемый показатель играет в астрономической науке важную роль и продолжает исследоваться и изучаться.

Источник

Как измерить массу Земли и массу Солнца?

Простая и надежная методика измерения массы космических тел — как узнать сколько весит Солнце, зная лишь силу притяжения между космическими телами

Как можно измерить вес (точнее, массу) Солнца, если даже реальный размер нашей “домашней звезды” настолько велик, что просто не укладывается в голове? Наверняка тут должен быть какой-то секрет… И подумав так, вы будете правы и не правы одновременно.

На первый взгляд, идея измерить массу Солнца, кажется фантастикой. На самом деле для этого не понадобится ничего, кроме простейших вычислений

С одной стороны, никакого секрета в деле измерения массы любого небесного тела сколько угодно большого размера, конечно же нет. С другой стороны, без определенных хитростей тут, конечно, не обойтись.

Давайте сразу условимся – говоря, что “нам нужно определить массу Солнца”, мы имеем ввиду “определить количество вещества входящего в состав Солнца”.

Для начала измерим массу Земли

Переформулировав задачу таким образом, мы сразу же получим зацепки ведущие к решению. Первым делом нам нужно определить величину силы притяжения возникающей между любыми двумя массами.

Принцип этого определения следующий:

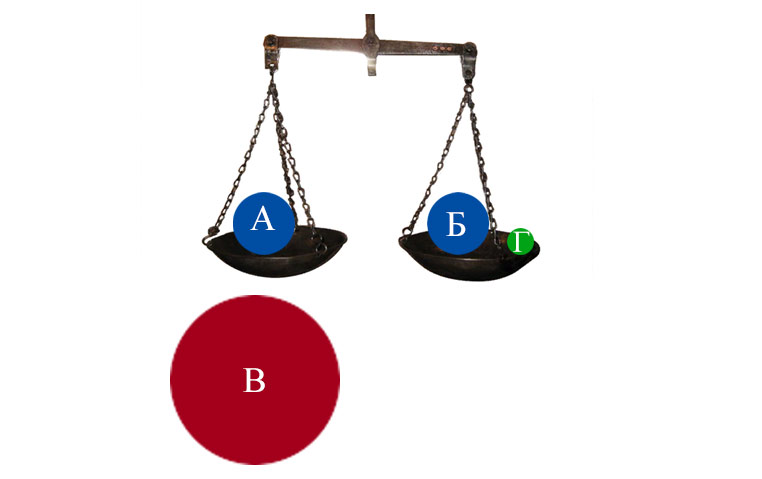
Представьте себе очень при очень чувствительные равноплечие весы с двумя чашками. В каждой чашке (А и Б) пускай лежит некий груз имеющий совершенно одинаковую массу. Весы в таком случае, будут прибывать в полном равновесии.

Теперь мы берем третье тело (В) масса которого нам также известна, и помещаем его под тело А. Взаимное притяжение между А и В, ожидаемо заставляет чашку весов А опуститься вниз. Для сохранения равновесия нам срочно необходимо добавить к массе Б очень небольшую, но опять же вполне измеримую массу Г.

Как вычислить массу планеты Земля, не выходя из дома?

Вас может заинтересовать

А вот теперь самое интересное: поскольку сила, с которой вся Земля притягивает тело Г, равна взаимному притяжению между А и В, можно без труда определить массу Земли, которая оказывается равной 6,59 х 10 21 тонн.

А теперь измерим массу Солнца!

Земля по своей орбите движется примерно так, как если бы невидимая нить соединяла ее с Солнцем. Действительно, гравитационное притяжение подобно натяжению нити, так что Земля все время движется к Солнцу, вместо того чтобы «улететь» по прямой линии, что будет, если эта “нить” вдруг оборвется. Можно сказать, что, двигаясь вокруг Солнца, Земля все время «падает» на него.

Этому “падению” соответствует отклонение ее орбиты от прямой линии, составляющее около 3 мм в секунду. Еще со времен Галилея известно, что на поверхности Земли в первую секунду своего падения всякое тело проходит 4,9 м. Расстояния 3 мм и 4,9 м прямо пропорциональны соответствующим гравитационным ускорениям, т. е. силам, действующим на единичную
массу со стороны Солнца на расстоянии Земли и Земли на ее поверхности.

Отсюда, зная, что гравитационное ускорение прямо пропорционально массе и обратно пропорционально квадрату расстояния от центра тела, можно легко вычислить, что масса Солнца в 329 390 раз больше массы Земли.

Воспользовавшись значением массы Земли, полученным выше, находим, что масса Солнца составляет 2.24 х 10 27 тонн. Полностью это немыслимое число можно записать, как 2 240 000 000 000 000 000 000 000 000 тонн.

Влияние силы тяготения на движение Земли. Путь А-С представляет собой путь пройденный Землей по орбите за 1 секунду (30 км), при этом отклонение от прямой линии B-C составит всего 3 миллиметра

Теперь уже можно вычислить и среднюю плотность Солнца, т. е. его массу, поделенную на массу воды, занимающей тот же объем.

Поскольку один кубический сантиметр воды весит один грамм, мы просто должны разделить массу Солнца (в граммах) на его объем (в кубических сантиметрах). Получим в результате число 1,42.

Иными словами, в среднем некоторый объем солнечного вещества должен весить приблизительно столько же, сколько ком битумного угля, занимающего такой же объем.

Естественно, “среднее значение” на то и среднее, чтоб представлять некую золотую середину между солнечным ядром (где плотность вещества в 10 раз превышает плотность стали) и веществом солнечной короны (где плотность падает почти до величины космического вакуума). Тем не менее, в общем и целом данная методика расчетов абсолютно верна и может с успехом применяться при расчете массы любого небесного тела – хоть астероида, хоть звезды.

Источник

Как ученые посчитали массу Солнца?

На любое тело действуют две силы или две «скорости» — сила тяготения (маленький объект падает на большой) и, собственно, скорость, с которой этот объект летит «прямо».

Первая картинка из гугла с какой-то там задачи вполне подходит для пояснения.

Если скорость большая — то тело совершает дугу и улетает. Как делают кометы.

То есть, вот она летела-летела, начала притягиваться, но поскольку летела слишком быстро, не успела упасть, а сделала дугу и улетела дальше.

Если сила тяготения большая — то тело просто падает.

А вот если оно летает по кругу — значит, эти две силы равны между собой. Земля пытается улететь, но её по чуть-чуть притягивает к себе Солнце, постоянно изменяя её траекторию вплоть до замкнутого состояния.

Центростремительная сила вычисляется по формуле F=ma. Где массу Земли мы знаем (вычислили по ходу развития науки), а ускорение — вычисляется из того, что Земля делает один оборот за год.

И, как я уже объяснил выше, эта сила должна быть равна силе тяготения. Ну а тяготение рассчитывается исходя из массы двух тел. И зная массу Земли, расстояние до Солнца, и силу, которая на Землю действует, мы спокойно можем вычислить массу Солнца.

Для расчёта в наше время хватает буквально школьного уровня знаний.

По примерно такой же методике вычисляется и масса любых других объектов — спутников, вращающихся вокруг планеты, других планет, вращающихся вокруг звёзд, самих звёзд, взаимодействующих друг с другом и так далее.

Источник

Как определяют массу солнца

Коэффициент пропорциональности G = наз. гравитационной постоянной или постоянной тяготения. Её находят из физического эксперимента с крутильными весами, позволяющими определить силу гравитац. взаимодействия тел известной массы.

В случае свободного падения тел сила F, действующая на тело, равна произведению массы тела на ускорение свободного падения g. Ускорение g может быть определено, напр., по периоду T колебаний вертикального маятника: , где l — длина маятника. На широте 45 o и на уровне моря g= 9,806 м/с 2 .

Подстановка выражения для сил земного притяжения в ф-лу (1) приводит к зависимости , где — масса Земли, а — радиус земного шара. Таким путём была определена масса Земли г. Определение массы Земли явл. первым звеном в цепи определений масс др. небесных тел (Солнца, Луны, планет, а затем и звёзд). Массы этих тел находят, опираясь либо на 3-й закон Кеплера (см. Кеплера законы ), либо на правило: расстояния к.-л. масс от общего центра масс обратно пропорциональны самим массам. Это правило позволяет определить массу Луны. Из измерений точных координат планет и Солнца найдено, что Земля и Луна с периодом в один месяц движутся вокруг барицентра — центра масс системы Земля — Луна. Расстояние центра Земли от барицентра равно 0,730 (он расположен внутри земного шара). Ср. расстояние цeнтpa Луны от центра Земли составляет 60,08 . Отсюда отношение расстояний центров Луны и Земли от барицентра равно 1/81,3. Поскольку это отношение обратно отношению масс Земли и Луны, масса Луны
г.

Массу Солнца можно определить, применив 3-й закон Кеплера к движению Земли (вместе с Луной) вокруг Солнца и движению Луны вокруг Земли:
, (2)
где а — большие полуоси орбит, T — периоды (звёздные или сидерические) обращения. Пренебрегая по сравнению с , получим отношение , равное 329390. Отсюда г, или ок. .

Аналогичным путём определяют массы планет, имеющих спутников. Массы планет, не имеющих спутников, определяют по возмущениям, к-рые они оказывают на движение соседних с ними планет. Теория возмущённого движения планет позволила заподозрить существование тогда неизвестных планет Нептуна и Плутона, найти их массы, предсказать их положение на небе.

Массу звезды (помимо Солнца) можно определить со сравнительно высокой надёжностью только в том случае, если она явл. физ. компонентом визуально-двойной звезды (см. Двойные звезды ), расстояние до к-рой известно. Третий закон Кеплера в этом случае даёт сумму масс компонентов (в ед. ):
,
где а» -большая полуось (в секундах дуги) истинной орбиты спутника вокруг главной (обычно более яркой) звезды, к-рую в этом случае считают неподвижной, Р — период обращения в годах, — параллакс системы (в секундах дуги). Величина даёт большую полуось орбиты в а. е. Если можно измерить угловые расстояния компонентов от общего центра масс, то их отношение даст величину, обратную отношению масс: . Найденная сумма масс и их отношение позволяют получить массу каждой звезды в отдельности. Если компоненты двойной имеют примерно одинаковый блеск и сходные спектры, то полусумма масс даёт верную оценку массы каждого компонента и без дополнит. определения их отношения.

Для др. типов двойных звезд (затменно-двойных и спектрально-двойных) имеется ряд возможностей приблизительно определить массы звёзд или оценить их нижний предел (т.е. величины, меньше которых не могут быть их массы).

Совокупность данных о массах компонентов примерно ста двойных звёзд разных типов позволила обнаружить важную статистич. зависимость между их массами и светимостями (см. Масса-светимость зависимость ). Она даёт возможность оценивать массы одиночных звёзд по их светимостям (иначе говоря, по их абс. звёздным величинам ). Абс. звёздные величины М определяются по ф-ле: M = m + 5 + 5 lg — A(r) , (3) где m — видимая звёздная величина в выбранном оптич. диапазоне (в определённой фотометрич. системе, напр. U, В или V; см. Астрофотометрия ), — параллакс и A(r) — величина межзвёздного поглощения света в том же оптич. диапазоне в данном направлении до расстояния .

Если параллакс звезды не измерен, то приближённое значение абс. звёздной величины можно определить по её спектру. Для этого необходимо, чтобы спектрограмма позволяла не только узнать спектральный класс звезды, но и оценить относительные интенсивности нек-рых пар спектр. линий, чувствительных к «эффекту абс. величины». Иначе говоря, сначала необходимо определить класс светимости звезды — принадлежность к одной из последовательностей на диаграмме спектр-светимость (см. Герцшпрунга-Ресселла диаграмма ), а по классу светимости — её абс. величину. По полученной таким образом абс. величине можно найти массу звезды, воспользовавшись зависимостью масса-светимость (этой зависимости не подчиняются лишь белые карлики и пульсары ).

Ещё один метод оценки массы звезды связан с измерением гравитац. красного смещения спектр. линий в её поле тяготения. В сферически-симметричном поле тяготения оно эквивалентно доплеровскому красному смещению , где — масса звезды в ед. массы Солнца, R — радиус звезды в ед. радиуса Солнца, а выражено в км/с. Это соотношение было проверено по тем белым карликам, к-рые входят в состав двойных систем. Для них были известны радиусы, массы и истинные лучевые скорости v_r, являющиеся проекциями орбитальной скорости.

Невидимые (тёмные) спутники, обнаруженные около нек-рых звёзд по наблюдённым колебаниям положения звезды, связанным с её движением около общего центра масс (см. Невидимые спутники звезд ), имеют массы меньше 0,02 . Они, вероятно, не явл. самосветящимися телами и больше похожи на планеты.

Из определений масс звёзд выяснилось, что они заключены примерно в пределах от 0,03 до 60 . Наибольшее количество звёзд имеют массы от 0,3 до 3 . Ср. масса звезд в ближайших окрестностях Солнца , т.е. 10 33 г. Различие в массах звёзд оказывается много меньшим, чем их различие в светимостях (последнее может достигать десятков млн.). Сильно отличаются и радиусы звёзд. Это приводит к разительному различию их ср. плотностей: от до г/см 3 (ср. плотность Солнца 1,4 г/см 3 ).

Массу рассеянного звёздного скопления можно определить, сложив массы всех его членов, светимости к-рых определяют по их видимому блеску и расстоянию до скопления, а массы — по зависимости масса-светимость.

Массу шарового звёздного скопления далеко не всегда можно оценить путём подсчёта звёзд, т.к. в центральной области большинства таких скоплений изображения отдельных звёзд на фотографиях, полученных с оптимальной экспозицией, сливаются в одно светящееся пятно. Есть методы оценки общей массы всего скопления, основанные на статистич. принципах. Так, напр., применение теоремы о вириале (см. Вириала теорема ) позволяет оценить массу скопления (в ) по радиусу скопления r (пк) и ср. квадратич. отклонению лучевой скорости отдельных звёзд (в км/с) от ср. её значения (т.е. от лучевой скорости скопления как целого):
.

Если же подсчёт звёзд — членов шарового скопления возможен, то общую массу скопления можно определить как сумму произведений , где — функция светимости этого скопления, т.е. число звёзд, приходящихся на различные интервалы абс. звёздных величин M_i (обычно их подсчитывают в интервалах, равных 1 m ), a — масса, соответствующая данной абс. звёздной величине M_i по зависимости масса-светимость. Т.о., общая масса скопления , где сумма взята от самых ярких до самых слабых членов скопления.

Метод определения массы Галактики исходит из факта вращения Галактики. Устойчивость вращения позволяет предположить, что центростремит. ускорение для каждой звезды, в частности для Солнца, определяется притяжением вещества Галактики в пределах солнечной орбиты. Солнце притягивается к галактич. центру с силой , где R₀ — расстояние Солнца от ядра Галактики, равное см. Сила F₀ сообщает Солнцу ускорение , к-рое равно центробежному ускорению Солнца (без учёта влияния внеш. части Галактики и при условии эллипсоидальности поверхностей равной плотности по внутр. её части). Собственная галактич. скорость Солнца (т.н. круговая скорость на расстоянии R₀ от центра) 220 км/с, отсюда см/с 2 . Масса Галактики, без учёта её частей, внешних по отношению к галактической траектории Солнца, г. Масса Галактики в сферич. объёме с радиусом 15 кпк, согласно подобным расчётам, равна . При этом учитывается также масса всей диффузной (рассеянной) материи в Галактике.

Масса спиральной галактики может быть определена по результатам изучения её вращения, напр. из анализа кривой лучевых скоростей, измеренных в различных точках большой оси видимого эллипса галактики. В каждой точке галактики центростремит. сила пропорциональна массе более близких к центру галактики областей и зависит от закона изменения плотности галактики с удалением от её центра. Спектроскопич. наблюдения в оптич. диапазоне позволили построить кривые вращения спиральных галактик до расстояний 20-25 кпк от центра (а у ряда галактик высокой светимости до 40 кпк и более). Вплоть до этих расстояний круговая скорость не уменьшается с увеличением R, т.е. масса галактики продолжает расти с расстоянием. Т.о., в галактиках имеется скрытая масса . Масса невидимого (несветящегося) вещества галактик может в 10 и более раз превосходить массу светящегося вещества; предположительно, скрытая масса может существовать в форме очень слабых маломассивных звёзд или чёрных дыр или в форме элементарных частиц (напр., нейтрино , если они обладают массой покоя).

Для медленно вращающихся галактик, какими явл., напр., эллиптич. галактики, трудно получить кривые лучевых скоростей, но зато можно по расширению спектр. линии оценить ср. скорость звёзд в системе и, сопоставив её с истинными размерами галактики, определить её массу. Чем больше ср. скорость звёзд, тем больше должна быть масса галактики (при одинаковых размерах). Зависимость между массой, размерами галактики и ср. скоростью звёзд вытекает из условия стационарности системы.

Ещё один способ оценки массы галактик-компонентов двойных систем аналогичен методу оценки масс компонентов спектрально-двойных звёзд (ошибка не превышает 20%). Используют также установленную статистич. зависимость между массой и интегр. светимостью галактик различного типа (своего рода зависимость масса-светимость для галактик). Светимость определяется по видимой интегр. звёздной величине и расстоянию, к-рое оценивается по красному смещению линий в спектре. Ср. масса галактик, входящих в скопление галактик, оценивается по числу галактик скопления и его общей массе, к-рую статистически определяют по дисперсии лучевых скоростей галактик, подобно тому как оценивается общая масса звёздного скопления на основе теоремы о вириале.

Известные ныне массы галактик заключены в пределах от

10 5 (т.н. карликовые галактики) до 10 12 (сверхгигантские эллиптич. галактики, напр. галактика М 87), т.е. отношение масс галактик доходит до 10 7 .

Точность определения масс астрономич. объектов зависит от точности определения всех величин, входящих в соответствующие ф-лы. Масса Земли определена с погрешностью 0,05%, масса Луны 0,1%. Погрешность определения массы Солнца также составляет 0,1%, она зависит от точности определения астрономической единицы (ср. расстояния до Солнца). Вообще, в значит. степени точность определения массы зависит от точности измерения расстояния до космического объекта , в случае двойных звёзд — от расстояния между ними, от линейных размеров тел и т.д. Массы планет известны с погрешностью от 0,05 до 0,7%. Массы звёзд определены с погрешностью от 20 до 60%. Неуверенность определения масс галактик можно характеризовать коэфф. 2-5 (масса может быть в неск. раз больше или меньше), если надёжно определено расстояние до них.

Лит.:
Струве О., Линде Б., Пилланс Э., Элементарная астрономия, пер. с англ., 2 изд., М., 1967; Сагитов М.У., Постоянная тяготения и масса Земли, М., 1969; Климишин И.А., Релятивистская астрономия, М., 1983.

Источник