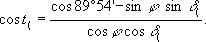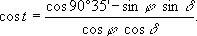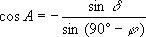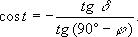Расчет кажущегося положения Солнца
Теперь можно рассчитать кажущееся положение Солнца: высотаh и азимут А — в любой точке на широте φ в любое время суток в соответствии с углом τ и в любое время года в соответствии с углом склонения δ.
Мы же приведем результат в простейшем виде:
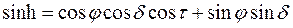
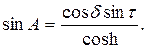
где φ — географическая широта ;
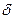
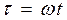
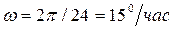
где 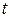
Очевидно, в полдень высота Солнца h максимальна, h = 90° -φ +δ.
Во время летнего солнцестояния высота Солнца в нашей местности в момент кульминации составляет: h = 90˚- φ + δ☼ = 90˚ — 56,5˚ +23,5˚=57˚, во время зимнего солнцестояния h = 90˚- φ + δ☼= 90˚ — 56,5˚ — 23,5˚=10˚, а в дни равноденствий, когда Солнце находится на небесном экваторе- δ☼=0, h = 33,5˚.
Часовой угол захода(восхода) Солнца
При восходе и заходе Солнца h = 0. Из уравнения (3.4) видно, что это произойдет при углах τ в каждом из двух случаев, близких к полудню, для которых при h = 0 из уравнение имеем:
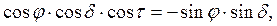
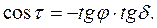
Тогда часовой угол захода (восхода) Солнца для горизонтальной поверхности
τ=arccos(-tg 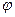
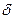
ЛЕКЦИЯ 5
Тема: Фотоэлектрические преобразование солнечной энергии
Источник
Вычисление моментов времени и азимутов восхода и захода светил
Часовой угол светила определяется из первой формулы (1.37), а именно:
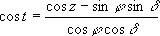
Если какая-нибудь точка небесного свода восходит или заходит, то она находится на горизонте и, следовательно, ее видимое зенитное расстояние z’ = 90°. Ее истинное зенитное расстояние z в этот момент вследствие рефракции будет больше видимого на величину 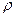
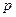
z = z’ +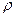
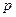
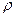
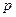
Кроме того, для Солнца и Луны, имеющих заметные размеры, координаты относятся к центру их видимого диска, а восходом (или заходом) этих светил считается момент появления (пли исчезновения) на горизонте верхней точки края диска. Следовательно, истинное зенитное расстояние центра диска этих светил в момент восхода или захода будет больше зенитного расстояния верхней точки края диска на величину видимого углового радиуса R диска. (У Солнца и Луны их видимые угловые радиусы приблизительно одинаковы и в среднем равны 16’.)
Таким образом, при вычислении часового угла светила в момент его восхода и захода в формуле (1.41), в самом общем случае, z = 90°+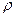
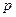
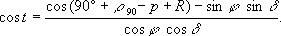
По формуле (1.42) часовые углы восхода и захода вычисляются только для Луны. В этом случае RR = 16’, рR = 57’ и 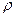
При вычислении часовых углов восхода и захода Солнца его горизонтальным параллаксом можно пренебречь, и при R ¤ = 16′ и 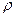

Для звезд и планет можно пренебречь также и их видимыми радиусами и вычислять часовые углы восхода и захода по формуле
Наконец, если пренебречь и рефракцией, то часовой угол восхода и захода вычисляется по формуле
cos t = — tg 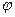

Каждое из приведенных уравнений дает два значения часового угла: t1= t и t2= — t. Положительное значение соответствует заходу, отрицательное — восходу светила. Местное звездное время восхода и захода, согласно формуле (1.15), получается таким:
sвосх = 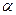
sзах = 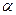
Затем можно вычислить моменты восхода и захода светила по местному среднему солнечному времени и по декретному времени.
Если вычисляется восход и заход Солнца, то нет необходимости вычислять звездное время явлений, так как, увеличив часовые углы t1 и t2 на 12h, мы сразу получаем моменты по местному истинному солнечному времени Т¤ = t¤ + 12h. Тогда местное среднее время
где h — уравнение времени, которое берется, так же как 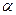

Азимуты точек восхода и захода светил (без учета рефракции, параллакса и углового радиуса) получим, если в первой формуле (1.36) положим z = 90°; тогда cos z = 0, sin z =1 и
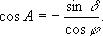
По формуле (1.45) получаем два значения азимута: А1 = A и A2 = 360° — A. Первое значение является азимутом точки захода, второе — азимутом точки восхода светила.
Представим теперь формулы (1.45) и (1.44) в виде
Так как косинус не может быть больше 1, то из этих формул следует, что восход и заход светила возможны только при условии
| 
| | | следующая лекция ==> | |
| Суточный параллакс | | | Лекция 4 СРЕДСТВА ФОРМИРОВАНИЯ ФИЗИЧЕСКОЙ КУЛЬТУРЫ ЛИЧНОСТИ |
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Как определить восход и заход солнца для своего населенного пункта
Иногда, например, отправляясь в пеший поход, нам крайне важно знать время восхода и захода солнца. Хочется очутиться в цивилизованных местах еще засветло. Но как рассчитать, когда нам отправляться и когда возвращаться? Легко! Посмотрите на отрывной календарь. Там на каждый день указывается с точностью до минуты, когда солнце восходит и когда оно садится. Прибавьте к этому еще полчаса-час (в зависимости от удаления от экватора и ясной/пасмурной погоды) на утреннюю зарю и вечерние сумерки, и вы получите продолжительность светового дня.
Однако в этом совете – руководствоваться отрывным календарем – есть одно но. Так мы будем знать время восхода и заката, к примеру, в Москве, но отнюдь не в нашей местности. И тут мы должны перейти от лирики к сухому языку цифр. Готовы? Тогда читайте нашу статью и рассчитывайте время светового дня для своей местности.
Какие географические параметры задействованы при расчете
По отношению к нашей звезде планета Земля вращается со скоростью пятнадцать градусов в час. Свою наивысшую позицию на небосклоне Солнце занимает в полдень. И в этом пункте следует учесть поправку на возможное летнее время, когда хронометры многих стран своевольно (то есть без согласования с Космосом) переводят на час вперед. Тогда солнце находится в зените в час дня. Но и это еще не все.
Существует еще понятие «истинный полдень». Земля поделена на часовые пояса. Каждый из них – довольно обширная территория. Поэтому в населенных пунктах, расположенных к востоку или западу от часового меридиана (где полдень наступает ровно в 12:00), он наблюдается раньше или позже. Следует, таким образом, установить долготу, на которой находится интересующий нас населенный пункт. Чтобы определить восход/заход солнца, нам следует знать и широту местности относительно экватора.
Магические даты равноденствия и солнцестояния
Два раза в год Земля поворачивается к нашему светилу под углом 90 градусов. В этом году это произойдет 19 марта и 22 сентября. В эти дни в любой точке планеты восход и заход солнца будет происходить в шесть часов (утра и вечера соответственно). Вот когда удобно вычислять местное время! На севере сумерки и заря долго играют на небосводе. В тропических широтах солнце ныряет за горизонт быстро. Но не это главное. Ведь световой день может оптически стать меньше из-за простой облачности.
Следует запомнить еще две даты: зимнего и летнего солнцестояния. Для северного полушария 21 декабря является днем с самой продолжительной ночью. А 21 июня солнце не спешит покидать небосвод. В эту дату на северном полярном круге ночь не наступает, а 21 декабря – не сменяется днем. Но когда наступает рассвет в летнее и зимнее солнцестояние в интересующей нас местности?
Восход и заход солнца в Москве
Рассмотрим алгоритм вычисления продолжительности светового дня и, следовательно, времени рассвета и заката на примере столицы. Девятнадцатого марта в Москве, впрочем, как и везде на земном шаре, светло будет двенадцать часов. Но поскольку мегаполис расположен чуть восточнее часового меридиана UTC +3, солнце взойдет там не в 6:00, а в 6:38. И зайдет тоже в 18:38. Световой день продолжает увеличиваться, достигая своего апогея в семнадцать часов и двадцать пять минут 20 июня. Мы легко можем определить восход и заход солнца для Москвы в эту дату. Полдень там наступает в 12:38. Тогда получается, что солнце восходит в 3:48, а заходит в 21:13. Вы уже знаете отклонение от часового меридиана в вашем населенном пункте? Когда там наступает истинный полдень?
Восход и заход солнца в выбранном пункте
Даты равноденствия и солнцестояния могут быть отправными данными для расчетов. 20 марта и на полярном круге, и на экваторе солнце взойдет в 6:00, а закат будет в 18:00. Тут мы учитываем отклонение от часового меридиана. После весеннего равноденствия в Северном полушарии световой день начинает расти, достигая своего апогея 21 июня. На полярном круге восход и заход солнца происходит в 0:00. Следовательно, световой день продолжается двадцать четыре часа. А на экваторе все остается по-прежнему: рассвет в 6:00, закат в 18:00. Чем выше широта, тем на больший отрезок времени растет световой день, тем раньше всходит солнце и тем позже оно заходит.
Зная географические координаты пункта, легко высчитать время рассвета и заката. Выводим формулу. Узнаем, сколько дней между весенним равноденствием и летним солнцестоянием. Девяносто двое суток. Мы также знаем, сколько часов продолжается световой день в летнее солнцестояние. Допустим, восемнадцать часов. 18 – 12 = 6. Шесть часов делим на 92. Результат – это на сколько минут растет каждый световой день. Делим его на два. Это – насколько раньше восходит солнце по сравнению с вчерашним днем.
Источник
Вычисление моментов времени и азимутов восхода и захода светил
Часовой угол светила определяется из первой формулы (1.37), а именно:
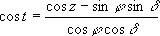
Если какая-нибудь точка небесного свода восходит или заходит, то она находится на горизонте и, следовательно, ее видимое зенитное расстояние z’ = 90°. Ее истинное зенитное расстояние z в этот момент вследствие рефракции будет больше видимого на величину 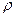
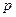
z = z’ +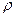
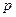
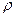
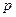
Кроме того, для Солнца и Луны, имеющих заметные размеры, координаты относятся к центру их видимого диска, а восходом (или заходом) этих светил считается момент появления (пли исчезновения) на горизонте верхней точки края диска. Следовательно, истинное зенитное расстояние центра диска этих светил в момент восхода или захода будет больше зенитного расстояния верхней точки края диска на величину видимого углового радиуса R диска. (У Солнца и Луны их видимые угловые радиусы приблизительно одинаковы и в среднем равны 16’.)
Таким образом, при вычислении часового угла светила в момент его восхода и захода в формуле (1.41), в самом общем случае, z = 90°+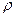
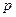
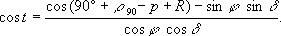
По формуле (1.42) часовые углы восхода и захода вычисляются только для Луны. В этом случае RR = 16’, рR = 57’ и 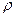
При вычислении часовых углов восхода и захода Солнца его горизонтальным параллаксом можно пренебречь, и при R ¤ = 16′ и 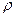

Для звезд и планет можно пренебречь также и их видимыми радиусами и вычислять часовые углы восхода и захода по формуле
Наконец, если пренебречь и рефракцией, то часовой угол восхода и захода вычисляется по формуле
cos t = — tg 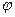

Каждое из приведенных уравнений дает два значения часового угла: t1= t и t2= — t. Положительное значение соответствует заходу, отрицательное — восходу светила. Местное звездное время восхода и захода, согласно формуле (1.15), получается таким:
sвосх = 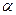
sзах = 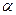
Затем можно вычислить моменты восхода и захода светила по местному среднему солнечному времени и по декретному времени.
Если вычисляется восход и заход Солнца, то нет необходимости вычислять звездное время явлений, так как, увеличив часовые углы t1 и t2 на 12h, мы сразу получаем моменты по местному истинному солнечному времени Т¤ = t¤ + 12h. Тогда местное среднее время
где h — уравнение времени, которое берется, так же как 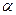

Азимуты точек восхода и захода светил (без учета рефракции, параллакса и углового радиуса) получим, если в первой формуле (1.36) положим z = 90°; тогда cos z = 0, sin z =1 и
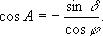
По формуле (1.45) получаем два значения азимута: А1 = A и A2 = 360° — A. Первое значение является азимутом точки захода, второе — азимутом точки восхода светила.
Представим теперь формулы (1.45) и (1.44) в виде
Так как косинус не может быть больше 1, то из этих формул следует, что восход и заход светила возможны только при условии
| 
| | | следующая лекция ==> | |
| Суточный параллакс | | | Лекция 4 СРЕДСТВА ФОРМИРОВАНИЯ ФИЗИЧЕСКОЙ КУЛЬТУРЫ ЛИЧНОСТИ |
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник