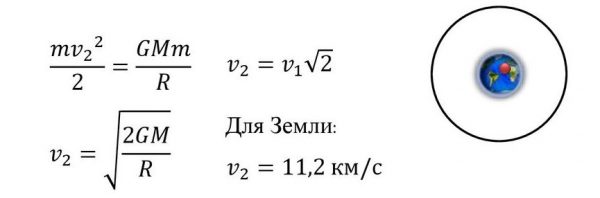Урок 11
| Космическая скорость | Формула | Величины, обозначенные в формулах буквами | Скорости, км/с |
| Первая | $v_1=\dfrac | $v_1$ — первая космическая скорость, $v_2$ — вторая космическая скорость, $v_3$ — третья космическая скорость, $v_<зем>$ — скорость Земли по орбите вокруг Солнца, $r$ — радиус Земли, $G$ — гравитационная постоянная, $M$ — масса Земли | $7.9$ |
| Вторая | $v_2=\dfrac | $11.2$ | |
| Третья* | $v_3=\sqrt | $16.7$ |
Проанализируйте записанные формулы и сделайте выводы.
Космические скорости для поверхностей других небесных тел зависят от масс небесных тел и их радиусов.
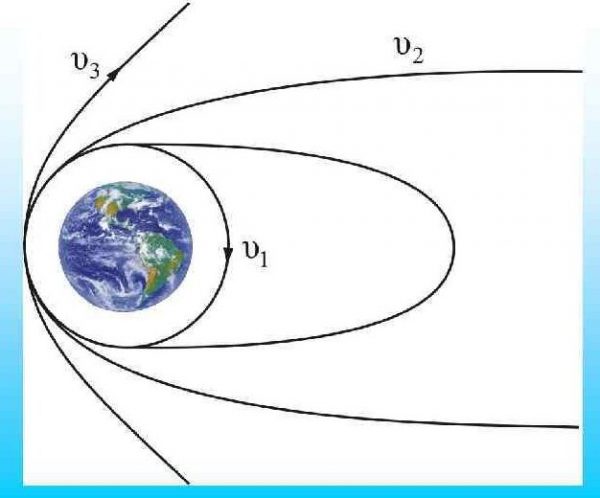
Траекторией движения тел является:
- а) окружность
- б) парабола относительно Земли
- в) гипербола относительно Земли и парабола относительно Солнца
а) первая космическая скорость для Луны:
б) вторая космическая скорость для Луны:
$v_1=\sqrt<2>·v_1;$ $v_1=\sqrt<2>·1,68=2,38$ км/с
Нет, так как наименьший период обращения искусственного спутника Земли равен $84,4$ мин, что видно из следующего расчёта:
Орбита — траектория, по которой движется небесное тело в космическом пространстве в поле тяготения других небесных тел и их систем.
Апогей — наиболее удалённая от Земли точка орбиты Луны или искусственного спутника Земли.
Перигей — ближайшая к Земле точка орбиты Луны или искусственного спутника Земли.
Эксцентриситет орбиты — мера сплюснутости эллипса, равная отношению расстояния между фокусами к большей оси эллипса.
Источник
Космические скорости
Любой предмет, будучи подброшенным вверх, рано или поздно оказывается на земной поверхности, будь то камень, лист бумаги или простое перышко. В то же время, спутник, запущенный в космос полвека назад, космическая станция или Луна продолжают вращаться по своим орбитам, словно на них вовсе не действует сила притяжения нашей планеты. Почему так происходит?
На нашей Земле всемирное тяготение воздействует на любое материальное тело. Тогда логично будет предположить, что есть некая сила, нейтрализующая действие гравитации. Эту силу принято называть центробежной.
Центробежную силу легко ощутить привязав на один конец нитки небольшой груз и раскрутив его по окружности. При этом чем больше скорость вращения тем сильнее натяжение нити, а чем медленнее вращаем мы груз тем больше вероятность, что он упадет вниз.
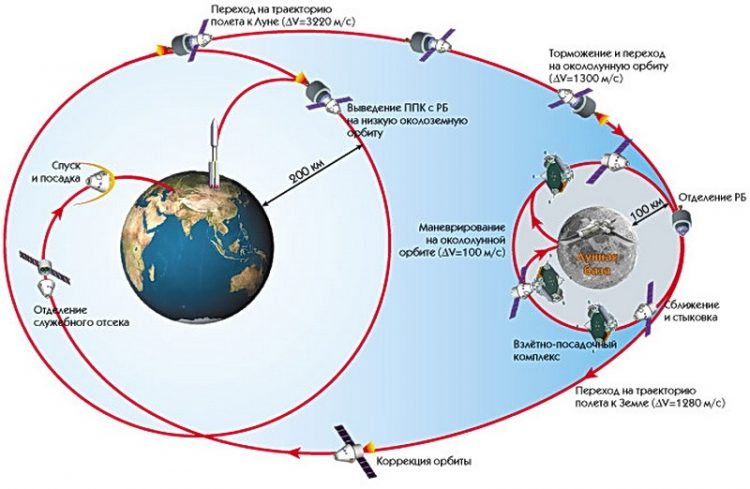
Траектория полета космических кораблей
Таким образом мы вплотную приблизились к понятию «космическая скорость». Простыми словами — это скорость, позволяющая любому объекту преодолеть тяготение небесного тела и их системы. Космические скорости используются для характеристики типа движения космического аппарата в сфере действия небесных тел: Солнца, Земли и Луны, других планет и их естественных спутников, а также астероидов и комет.
Это также значит, что космическая скорость есть у каждого объекта, который движется по орбите. Размер и форма орбиты космического объекта зависят от величины и направления скорости, которую данный объект получил на момент выключения двигателей, и высоты, на которой произошло данное событие.
Космическая скорость (первая v1, вторая v2, третья v3 и четвёртая v4) — это минимальная скорость, при которой какое-либо тело в свободном движении сможет:
- v1 — стать спутником небесного тела (то есть способность вращаться по орбите вокруг небесного тела и не падать на его поверхность);
- v2 — преодолеть гравитационное притяжение небесного тела и начать двигаться по параболической орбите;
- v3 — покинуть при запуске планету, преодолев притяжение Звезды;
- v4 — при запуске из планетной системы объект покинул Галактику.
Космические скорости могут быть рассчитаны для любого удаления от центра Земли. Однако в космонавтике часто используются величины, рассчитанные конкретно для поверхности шаровой однородной модели Земли радиусом 6371 км.
Первая космическая скорость
Первая космическая скорость или Круговая скорость V1 — скорость, которую необходимо придать объекту без двигателя, пренебрегая сопротивлением атмосферы и вращением планеты, чтобы вывести его на круговую орбиту с радиусом, равным радиусу планеты.
Иными словами, первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.
Формула
где G — гравитационная постоянная (6,67259·10−11 м³·кг−1·с−2), — первая космическая скорость. Подставляя численные значения (для Земли M = 5,97·1024 кг, R = 6 378 км), найдем
7,9 км/с
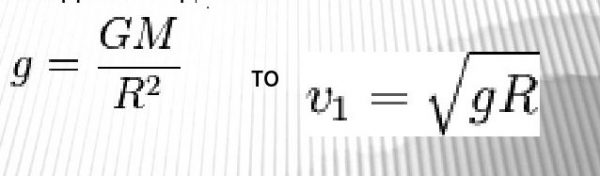
Первую космическую скорость можно определить через ускорение свободного падения —
Вторая космическая скорость
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость, которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела.
Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой:
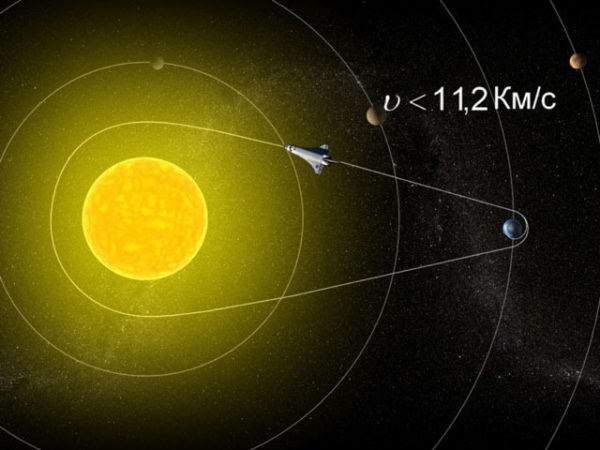
- для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца.
- для Солнца вторая космическая скорость составляет 617,7 км/с.
- для Луны скорость убегания равна 2,4 км/с , несмотря на то, что в действительности для удаления тела на бесконечность с поверхности Луны необходимо преодолеть притяжение Земли, Солнца и Галактики.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе.
Формула
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты, если будет падать на неё из бесконечности. Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния .
Третья космическая скорость
Третья космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение Солнца и в результате уйти за пределы Солнечной системы.
Только на космических кораблях, которым доступны такие скорости, принципиально могут быть осуществлены пилотируемые межзвёздные перелёты к планетным системам других звёзд.
Взлетая с поверхности Земли и наилучшим образом используя орбитальное движение планеты космический аппарат может достичь третей космической скорости уже при 16,6 км/с относительно Земли, а при старте с Земли в самом неблагоприятном направлении его необходимо разогнать до 72,8 км/с.
Здесь для расчёта предполагается, что космический аппарат приобретает эту скорость сразу на поверхности Земли и после этого не получает негравитационного ускорения (двигатели выключены и сопротивление атмосферы отсутствует). Если к тому же учесть притяжение других планет, которое может как ускорить, так и притормозить аппарат, то диапазон возможных значений 3-й космической скорости станет еще больше.
При наиболее энергетически выгодном старте скорость объекта должна быть сонаправлена скорости орбитального движения Земли вокруг Солнца. Орбита такого аппарата в Солнечной системе представляет собой параболу.
Четвёртая и пятая космическая скорости
Четвёртая космическая скорость — минимально необходимая скорость тела без двигателя, позволяющая преодолеть притяжение галактики Млечный Путь. Она используется довольно редко.
Четвёртая космическая скорость не постоянна для всех точек Галактики, а зависит от расстояния до центральной массы.
Для нашей галактики таковой является объект Стрелец A*, сверхмассивная чёрная дыра.
По грубым предварительным расчётам в районе нашего Солнца четвёртая космическая скорость составляет около 550 км/с. Значение сильно зависит не только (и не столько) от расстояния до центра галактики, а от распределения масс вещества по Галактике, о которых пока нет точных данных, ввиду того что видимая материя составляет лишь малую часть общей гравитирующей массы, а все остальное — скрытая масса.
Ещё реже в некоторых источниках встречается понятие «пятая космическая скорость». Это скорость, позволяющая добраться до иной планеты звездной системы вне зависимости от разности плоскостей эклиптики планет. Например, для Солнечной системы и, конкретно, для Земли, чтобы орбита межпланетного перелета была перпендикулярной к земной орбите, нужна скорость запуска 43,6 километра в секунду.
Видео
Источник
Параболическая скорость. Изучение природы Луны
Н. В. Гончар
Изучение природы Луны. 11-й класс
Н.В.ГОНЧАР ,
с. Стретенка, Приморский кр.
Изучение природы Луны
Обилие данных о Луне создаёт некую методическую трудность при изучении её физической природы – изложить весь материал за время, отведённое школьной программой, оказывается невозможным. Мой опыт показывает, что содержание этих уроков должно сводиться к рассмотрению основных физических характеристик (размеров, массы, средней плотности, вращения, температуры, рельефа, особенностей строения поверхности) Луны и к раскрытию принципов тех методов, которыми они найдены. Важно также рассмотреть причины, обуславливающие отсутствие на Луне атмосферы. Для активизации учащихся и лучшего усвоения содержания следует предусмотреть и самостоятельную работу.
Материал предлагаю распределить следующим образом:
Урок 1. Физические характеристики Луны (размер, масса, средняя плотность, ускорение свободного падение, вращение, температура), методы их определения.
Урок 2. Отсутствие на Луне атмосферы, его причины, рельеф и строение лунной поверхности. (На эту тему, я считаю, надо отводить 2 ч вместо 1 ч, предусмотренного программой.)
Изложение материала на 1-м уроке я начинаю с уже известных учащимся сведений: среднего расстояния от Земли до Луны (a = 384 400 км) и видимого углового диаметра (d = 31« ) или углового радиуса ( = 15,5« 1/4°). На доске показываю заранее подготовленный чертёж. Предлагаю учащимся самостоятельно вычислить линейный радиус Луны по формуле R Л = a sin.
Из курса математики учащиеся знают, что синусы малых углов пропорциональны самим углам, поэтому можно считать sin = sin1°. Приняв 1/4° и найдя по таблице тригонометрических функций sin1° = 0,0175, получаем R З = 384 400 · 0,25 · 0,0175 1580 (км).
Указываю на приближённость полученного результата и поясняю причину: несколько занижено значение углового радиуса Луны. Записываю на доске принятое в науке число R Л = 1738 км, отмечаю допустимость ошибки в 2% при приближённых вычислениях и предлагаю учащимся выразить линейный радиус Луны через средний радиус Земли R З = 6371 км:
откуда делается вывод о том, что поперечник Луны примерно в 4 раза меньше земного.
Далее напоминаю, что массы небесных тел вычисляются по третьему обобщённому закону Кеплера путём сравнения движения их спутников, и объясняю, что этот метод применим и для определения массы Луны. Расчёт средней плотности Луны не провожу на уроке, только напоминаю, что средняя плотность Земли 5,52 · 10 3 кг/м 3 , пишу на доске значение средней плотности Луны (3,37 · 10 3 кг/м 3), и отношение этих плотностей.
Сравнив эти значения получаем Л = 0,61 З. Здесь следует обратить вним ание учащихся на то, что небольшая средняя плотность Луны свидетельствует об отсутствии у неё плотного ядра, аналогичного земному.
Масса Луны и её размеры определяют ускорение свободного падения и параболическую скорость (вторая космическая скорость) на лунной поверхности. Поясняю, что ускорение свободного падения можно найти из закона всемирного тяготения. Далее констатирую, что ускорение свободного падения на Луне в 6 раз меньше земного:
Параболическая скорость на поверхности Луны определяется по формуле известной из курса физики (расчёт параболической скорости выполняется при наличии времени).
Температура на Луне была установлена наземными наблюдениями: на дневном полушарии она достигает +130 °С, а на ночном понижается до –170 °С. Космические исследования, проведённые на Луне, подтвердили большое различие температур на её дневном и ночном полушариях.
В заключение урока учащиеся должны сделать общие выводы об основных характеристиках Луны в сравнении их с земными.
Домашнее задание: § 13 учебника Е.П.Левитана «Физика-11». – М.: Просвещение, 1994. Вопрос 1, с. 67 (письменно в тетрадь).
На 2-м уроке предлагаю ученикам назвать основные физические условия на Луне, перечислить физические характеристики. Затем приступаю к объяснению отсутствия атмосферы на Луне: сообщаю и записываю на доске значения средних квадратичных скоростей молекул водорода (2240 м/с), азота и угарного газа (по 600 м/с), кислорода (560 м/с). Подчёркивания, что все они превосходят первую космическую скорость (круговая скорость), поэтому выделяющиеся из лунных недр газы улетучиваются в космическое пространство. Вода же не может существовать в жидком состоянии без атмосферного давления.
Поясняю, что атмосфера и вода на Земле постепенно разрушают рельеф, а на Луне изменения рельефа очень слабые и вызываются слабой тектонической деятельностью и падением метеоритов. Работаем с лунным глобусом.
Обобщение и закрепление материала провожу путём самостоятельной работы учащихся с карточками: перечислить формы рельефа, видимые на фотографиях лунной поверхности; показать на лунной карте и назвать два-три моря, два-три кратера.
Далее сообщаю, что лабораторные исследования лунных пород показали сходство их химического состава с земными породами, что свидетельствует о материальном единстве Вселенной. Однако лунный грунт – реголит – более рыхлый. Весь остальной материал учащиеся изучают самостоятельно по учебнику Е.П.Левитана .
ОБ АВТОРЕ. Наталия Владимировна Гончар родилась и выросла в Алма-Ате. В 1985 г. окончила физфак Казахского ГПУ им. Абая. С 1988 г. живёт и работает в с. Стретенка Дальнереченского района Приморского края. С 1999 г. является директором школы. Сын – студент факультета прикладной информатики Дальневосточного ТУ.
Решебник по астрономии 11 класс на урок №11 (рабочая тетрадь) — Движение космических аппаратов
1. Запишите формулы, по которым определяют значения космических скоростей для поверхности земли, и объясните входящие в них величины.
Проанализируйте записанные формулы и сделайте выводы.
Космические скорости для поверхностей других небесных тел зависят от масс небесных тел и их радиусов.
Траекторией движения тел является:
а) окружность
б) парабола относительно Земли
в) гипербола относительно Земли и парабола относительно Солнца
2. Рассчитайте первую (а) и вторую (б) космические скорости для Луны (масса Луны m = 7.35*10 22 кг, а её радиус R = 1740 км).
Решение:
а) первая космическая скорость для Луны:

б) вторая космическая скорость для Луны:
3. Может ли период обращения искусственного спутника Земли, движущегося по законам Кеплера, быть T = 81 мин? Ответ аргументируйте.
Нет, так как наименьший период обращения искусственного спутника Земли равен 84.4 мин, что видно из следующего расчёта:
4. Дайте определение понятиям.
Орбита — траектория, по которой движется небесное тело в космическом пространстве в поле тяготения других небесных тел и их систем.
Апогей — наиболее удалённая от Земли точка орбиты Луны или искусственного спутника Земли.
Перигей — ближайшая к Земле точка орбиты Луны или искусственного спутника Земли.
Эксцентриситет орбиты — мера сплюснутости эллипса, равная отношению расстояния между фокусами к большей оси эллипса.
5. Укажите формы орбит небесных тел, если их эксцентриситеты принимают следующие значения:
6. Рассчитайте время полёта по полуэллиптической орбите: а) до Марса; б) до Венеры.
ГРАВИТАЦИОННОЕ ПОЛЕ 2 — ПАРАБОЛИЧЕСКАЯ СКОРОСТЬ
Чтобы ракета покинула Землю и смогла долететь до Луны или других планет, она должна развить скорость около 11 км/с. Минимальная скорость, необходимая для преодоления телом силы притяжения другого, более массивного тела, называется параболической. Относительно планет ее еще называют второй космической скоростью, или скоростью ухода. Если двигатели ракеты недостаточно мощные, то она не сможет развить эту скорость и останется на околопланетной орбите или упадет на планету.
Чтобы ракета массой m покинула планету массой М первой, нужна энергия, равная GMm/R, где R — радиус планеты. Ракета должна покинуть гравитационное притяжение планеты благодаря своей кинетической энергии, которая после выработки топлива равна GMm/R. Скорость ухода v yx должна быть такой, чтобы минимум кинетической энергии 1 / 2 mv 2 yx также равнялся GMm/R.
Таким образом, скорость ухода от поверхности планеты равна 2GM/R, или 2g s R, поскольку g s , сила тяжести у поверхности планеты, определяется по формуле GM/R 2 . У поверхности Земли g = 9,80 Н/кг, а R = 6370 км (приблизительно). Отсюда скорость ухода равна (2 x 9,80 x 6370 x 1000) = 11 200 м/с. У поверхности Луны g = 1,62 Н/кг и R = 1740 км, отсюда скорость ухода равна 2380 м/с. Так как параболическая скорость ухода от поверхности Луны значительно меньше, чем та же скорость у поверхности Земли, астронавты с корабля «Аполлон» могли стартовать с Луны с помощью значительно меньших модулей, чем ракета-носитель «Сатурн», которая стартовала с Земли.
У Земли есть атмосфера, у Луны нет. Молекулы газа в атмосфере Земли двигаются со скоростью, меньшей скорости ухода (11,2 км/с), и поэтому они не могут преодолеть силу земного притяжения. Молекулы газа у поверхности Луны имели бы тот же диапазон скоростей, что и молекулы газа у поверхности Земли, так как диапазон температур там приблизительно тот же, что и на Земле. Но они легко покинули бы Луну, так как скорость ухода от поверхности там значительно меньше.
Анализ второй космической скорости по Исаку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос.
Вторая космическая скорость (параболическая скорость, скорость убегания) — наименьшая скорость , которую необходимо придать объекту (например, космическому аппарату), масса которого пренебрежимо мала относительно массы небесного тела (например, планеты), для преодоления гравитационного притяжения этого небесного тела. Предполагается, что после приобретения телом этой скорости оно не получает негравитационного ускорения (двигатель выключен, атмосфера отсутствует).
Вторая космическая скорость определяется радиусом и массой небесного тела, поэтому она своя для каждого небесного тела (для каждой планеты) и является его характеристикой. Для Земли вторая космическая скорость равна 11,2 км/с. Тело, имеющее около Земли такую скорость, покидает окрестности Земли и становится спутником Солнца. Для Солнца вторая космическая скорость составляет 617,7 км/с.
Параболической вторая космическая скорость называется потому, что тела, имеющие вторую космическую скорость, движутся по параболе .
Вывод формулы
Для получения формулы второй космической скорости удобно обратить задачу — спросить, какую скорость получит тело на поверхности планеты , если будет падать на неё из бесконечности . Очевидно, что это именно та скорость, которую надо придать телу на поверхности планеты, чтобы вывести его за пределы её гравитационного влияния.
где слева стоят кинетическая и потенциальная энергии на поверхности планеты (потенциальная энергия отрицательна, так как точка отсчета взята на бесконечности), справа то же, но на бесконечности (покоящееся тело на границе гравитационного влияния — энергия равна нулю). Здесь m — масса пробного тела, M — масса планеты, R — радиус планеты, G — гравитационная постоянная , v 2 — вторая космическая скорость.
Разрешая относительно v 2 , получим
Между первой и второй космическими скоростями существует простое соотношение:
Квадрат скорости убегания равен удвоенному ньютоновскому потенциалу в данной точке (например, на поверхности планеты):

| Небесное тело | Небесное тело | Масса (по отношению к массе Земли | 2-я космическая скорость, км/с | ||
|---|---|---|---|---|---|
| Меркурий | 0,055 | 4,3 | Сатурн | 95,3 | 36,0 |
| Венера | 0,82 | 10,22 | Уран | 14,5 | 22,0 |
| Земля | 1 | 11,2 | Нептун | 17,5 | 24,0 |
| Марс | 0,108 | 5,0 | Луна | 0,0123 | 2,4 |
| Юпитер | 318,3 | 61,0 | Солнце | 333 000 | 617,7 |
| Сириус В | 325 675 | 10 000 | Нейтронная звезда | 666 000 | 200 000 |
| Кварковая звезда | 832 500 | 300 000 | Чёрная дыра | 832 500 — 5,6*10 15 | Бесконечность |
См. также
Wikimedia Foundation . 2010 .
Смотреть что такое «Параболическая скорость» в других словарях:
Минимальная скорость, которую нужно сообщить телу массой m (напр., космическому аппарату), чтобы оно могло преодолеть гравитационное притяжение другого тела массой М m (напр., Земли) и, двигаясь по параболической траектории, навсегда покинуть… … Большой Энциклопедический словарь
См. Космическиескорости. Физическая энциклопедия. В 5 ти томах. М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988 … Физическая энциклопедия
Минимальная скорость, которую нужно сообщить телу массой т (например, космическому аппарату), чтобы оно могло преодолеть гравитационное притяжение другого тела массой М>>т (например, Земли) и, двигаясь по параболической траектории, навсегда… … Энциклопедический словарь
параболическая скорость — parabolinis greitis statusas T sritis Standartizacija ir metrologija apibrėžtis Paraboline trajektorija judančio taško ar kūno greitis. atitikmenys: angl. parabolic velocity vok. parabolische Geschwindigkeit, f rus. параболическая скорость, f… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
параболическая скорость — parabolinis greitis statusas T sritis fizika atitikmenys: angl. parabolic velocity vok. parabolische Geschwindigkeit, f rus. параболическая скорость, f pranc. vitesse parabolique, f … Fizikos terminų žodynas
Скорость, которую нужно сообщить тому или иному телу (космическому зонду, частице атмосферы и т.п.), чтобы оно, преодолев притяжение Земли (Луны, планеты и др.), удалилось от неё по параболической орбите. П. с. уменьшается с расстоянием… … Большая советская энциклопедия
Источник