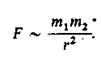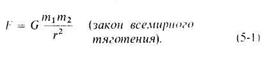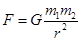Ускорение свободного падения на Земле и на Луне
Все тела притягиваются друг к другу — это закон всемирного тяготения. Силы, с которыми тела притягиваются вычисляются по формуле:
Здесь G — это гравитационная постоянная, равная 6,67 × 10 -11 Н · м 2 /кг 2 . Она численно равна силе, с которой одно тело массой 1 кг притягивает другое тело с массой 1 кг, находящееся от него на расстоянии 1 м. Как мы видим, это очень маленькая сила. Поэтому мы замечаем притяжение только к очень массивным телам, космического масштаба.
Если размеры одного тела несоизмеримо меньше размеров другого тела и оно находится на поверхности второго тела или на высоте намного меньше радиуса второго тела, то за расстояние между телами принимается радиус второго тела. (Притяжение всегда идет к центру тела.)
В результате действия закона всемирного тяготения планеты и другие космические тела притягивают к себе другие тела. Эта сила притяжения называется силой тяжести. Под ее действием падающим телам сообщается ускорение свободного падения (g). Сила тяжести вычисляется по формуле:
Подставим вместо F в первую формулу значение F из второй. При этом пусть m1 — это масса падающего на Землю тела. Обозначим ее как m. А m2 — это масса Земли. Обозначим ее как M. Тогда получим:
Разделим обе части формулы на m (массу падающего тела):
Мы видим, что ускорение свободного падения зависит от массы и радиуса планеты. Чем больше ее масса, тем сильнее она притягивает тела и тем больше на ней ускорение свободного падения. Чем больше радиус планеты, тем дальше от ее центра находится притягиваемое тело и тем меньше будет ускорение свободного падения.
Таким образом, чтобы сравнить ускорение свободного падения на Земле и Луне, надо сравнить отношения их масс к квадратам их радиусов. Но чтобы найти само ускорение свободного падения, надо еще умножить на гравитационную постоянную.
Масса Земли приблизительно равна 6 × 10 24 кг, а ее радиус приблизительно равен 6400 км (6,4 × 10 6 м). Поэтому ускорение свободного падения на Земле приблизительно будет равно:
g = 6,67 × 10 -11 Н × м 2 /кг 2 × 6 × 1024 кг ÷ (6,4 × 106 м) 2 ≈ 0,977 × 10 1 ≈ 9,8 Н/кг (м/c 2 )
Масса Луны примерно равна 7,5 × 10 22 кг, а ее радиус примерно равен 1750 км. Поэтому ускорение свободного падения на Луне приблизительно будет равно:
g = 6,67 × 10 -11 Н × м 2 /кг 2 × 7,5 × 10 22 кг ÷ (1,75 × 10 6 м) 2 ≈ 16,335 10 -1 ≈ 1,6 Н/кг (м/с 2 )
Отношение ускорений свободного падения на Земле и Луне равно 9,8 : 1,6 ≈ 6 : 1. Значит, сила притяжения тела с массой m на Луне будет примерно в 6 раз меньше, чем на Земле.
Источник
Пример 1. Чему равно ускорение Луны и каково отношение этого ускорения к ускорению свободного падения на поверхности Земли?
Чему равно ускорение Луны и каково отношение этого ускорения к ускорению свободного падения на поверхности Земли?
Решение: Используя формулу для центростремительного ускорения, находим, что ускорение Луны 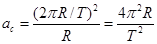
Вблизи поверхности Земли ускорение равно g = 9,8 м/с 2 .
Таким образом, отношение а/g = 1/3590 = (1/60) 2 .
Ньютон выполнил простые вычисления, близкие к описанным в примере 1, и обнаружил, что сила тяготения, действующая со стороны Земли на яблоко, удаленное к Луне, уменьшится в 3600 = (60) 2 раз, что соответствует отношению квадратов расстояний.
Отсюда Ньютон заключил, что сила тяготения между двумя телами должна убывать обратно пропорционально квадрату расстояния между ними.
Он предложил универсальный закон гравитационного притяжения между любыми двумя телами:
Для обозначения коэффициента пропорциональности используется прописная буква G. Таким образом,
Пример 2.
Предположив, что средняя плотность Земли равна ρ = 5 • 10 3 кг/м 3 , Ньютон нашел численное значение G. (Его догадка с точностью 10% совпала с истинным значением.) Получите выражение для G через ρ , rз и g.
Решение: Применим формулу (5-1)
к силе, действующей между Землей и яблоком.
Обозначим массу Земли Мз,
а массу яблока т.
Полагая r равным расстоянию rз между центром Земли и яблоком, имеем
В соответствии со вторым законом Ньютона эта сила должна равняться та, причем в нашем случае а = g. Таким образом,
Учитывая, что Mз равна произведению плотности на объем, т. е.
Подставляя сюда Rз = 6,37-10 6 м и ρ = 5 х 10 3 кг/м 3 , имеем
G = 7,35- 10 -11 Н -м 2 •кг -2 ,
что всего лишь на 10% превышает принятое значение
G = 6,67. 10 -11 Н -м 2 •кг -2
Сравнивая ускорение свободного падения на Луне с величиной этого ускорения на поверхности Земли, Ньютон предположил, что Земля ведет себя так, как если бы вся ее масса была сконцентрирована в центре. Ньютон догадался, что такое поведение справедливо в случае сил, изменяющихся обратно пропорционально квадрату расстояния. Однако ему удалось получить строгое доказательство лишь 20 лет спустя.
«Взвешивание –Земли»
Тяготение действует на огромных расстояниях.
Но закон Ньютона утверждает, что взаимно притягиваются все предметы.
А правда ли, что любые два предмета, притягивают друг друга?
Можем ли мы сами поставить такой опыт, а не гадать, глядя на небо, притягиваются ли планеты?
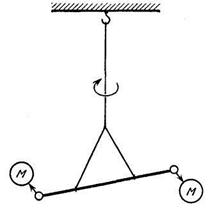
Такой прямой опыт сделал Кавендиш (1731 —1810) при помощи прибора, который показан на рис. 11. Идея состояла в том, чтобы подвесить на очень тонкой кварцевой нити стержень с двумя шарами и затем поднести к ним сбоку два больших свинцовых шара, как показано на рисунке. Притяжение шаров слегка перекрутит нить — слегка, потому что силы притяжения между обычными предметами очень слабы. Силу притяжения между двумя шарами можно измерить. Кавендиш назвал свой опыт «взвешиванием Земли».
Педантичный и осторожный преподаватель наших дней не позволит студентам так выразиться; нам пришлось бы сказать «измерение массы Земли». При помощи такого прибора Кавендишу удалось непосредственно измерить силу, расстояние и величину обеих масс и, таким образом, определить постоянную тяготения G.
Вы скажете: «Взвешивание Земли представляет собой почти такую же задачу. Мы знаем силу притяжения, знаем массу объекта, который притягивается, и знаем, насколько он удален, но мы не знаем ни массы Земли, ни постоянной тяготения, а только их произведение».
Измерив постоянную и зная, как Земля притягивает предметы, мы сможем вычислить ее массу.
Этот опыт впервые позволил косвенно определить, насколько тяжел, массивен шар, на котором мы живем. Результат его невольно вызывает удивление, и именно поэтому Кавендиш назвал свой опыт «взвешиванием Земли», а не «определением постоянной уравнения тяготения».
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Таблица Ускорение свободного падения на планетах солнечной системы
Ускорение свободного падения тел на Луне (естественный и единственный спутник планеты Земля) рассчитывается по формуле:
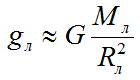
G — гравитационная постоянная, находится из закона всемирного тяготения и равна 6,67·10 -11 Н м 2 /кг 2
Mл — масса Луны;
Rл — радиус Луны.
Приведённая формула применима для расчёта ускорения свободного падения тела на планетах солнечной системы, в том числе и на планете Земля.
| Наименование планеты солнечной системы | Значение ускорения свободного падения, м/с 2 |
| Солнце | 274 |
| Юпитер | 25,8 |
| Нептун | 11,6 |
| Сатурн | 11,3 |
| Земля | 9,8 |
| Уран | 9 |
| Венера | 8,9 |
| Меркурий | 3,7 |
| Марс | 3,7 |
| Луна | 1,62 |
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.2 / 5. Количество оценок: 6
Источник
Как рассчитать ускорение свободного падения на Марсе и других космических телах
На стыке XVII и XVIII веков жил в Британии один ученый, Исаак Ньютон, отличавшийся большой наблюдательностью. Так случилось, что вид сада, где с веток на землю падали яблоки, помог ему открыть закон всемирного тяготения. Какая же сила заставляет плод все быстрее двигаться к поверхности планеты, по каким законам происходит это перемещение? Попытаемся ответить на эти вопросы.
А если бы эти яблони, как обещала в свое время советская пропаганда, росли на Марсе, каким бы тогда было это падение? Ускорение свободного падения на Марсе, на нашей планете, на других телах Солнечной системы. От чего оно зависит, каких величин достигает?
Ускорение свободного падения
Чем замечательна знаменитая Пизанская башня? Наклоном, архитектурой? Да. А еще с нее удобно бросать вниз различные предметы, чем и занимался в начале XVII века знаменитый итальянский исследователь Галилео Галилей. Бросая вниз всякие вещицы, он заметил, что тяжелый шар в первые мгновения падения двигается медленно, затем скорость его возрастает. Исследователя интересовал математический закон, по которому происходит изменение скорости.
Измерения, произведенные в дальнейшем, в том числе другими исследователями, показали, что скорость падающего тела:
- за 1 секунду падения становится равной 9,8 м/с;
- за 2 секунды – 19,6 м/с;
- 3 – 29,4 м/с;
- …
- n секунд – n∙9,8 м/с.
Эта величина 9,8 м/с∙с получила название «ускорение свободного падения». На Марсе (Красной планете) или другой планете это ускорение такое же или нет?
Почему на Марсе по-другому
Исаак Ньютон, рассказавший миру, что такое всемирное тяготение, смог сформулировать и закон ускорения свободного падения.
С развитием технологий, поднявших на новый уровень точность лабораторных измерений, ученые смогли подтвердить, что ускорение свободного падения на планете Земля – не такая уж и постоянная величина. Так, на полюсах она больше, на экваторе – меньше.
Ответ на эту загадку кроется в вышеуказанном уравнении. Дело в том, что земной шар, строго говоря, не совсем шар. Это эллипсоид, слегка приплюснутый с полюсов. Расстояние до центра планеты на полюсах меньше. А уж как отличается и массой, и размерами от земного шара Марс. Ускорение свободного падения на нем также будет иным.
Используя уравнение Ньютона и общеизвестные данные:
- масса планеты Марс − 6,4171·10 23 кг;
- средний диаметр − 3389500 м;
- гравитационная константа − 6,67∙10 -11 м 3 ∙с -2 ∙кг -1 .
Не составит труда найти ускорение свободного падения на Марсе.
g Марса = 6,67∙10 -11 ∙6,4171·10 23 / 3389500 2 = 3,71 м/с 2 .
Для проверки полученного значения можно заглянуть в любой справочник. Оно совпадает с табличным, значит, расчет произведен правильно.
Как ускорение свободного падения связано с весом
Вес – это сила, с которой любое тело, обладающее массой, давит на поверхность планеты. Измеряется он в ньютонах и равен произведению массы на ускорение свободного падения. На Марсе и любой другой планете оно, разумеется, будет отличаться от земного. Так, на Луне сила тяжести в шесть раз меньше, чем на поверхности нашей планеты. Это даже создавало определенные трудности у астронавтов, высадившихся на естественный спутник. Перемещаться оказалось удобнее, подражая кенгуру.
Итак, как было рассчитано, ускорение свободного падения на Марсе составляет 3,7 м/с 2 , или 3,7 / 9,8 = 0,38 от земного.
А означает это, что вес любого предмета на поверхности Красной планеты будет составлять лишь 38% от веса этого же предмета на Земле.
Как и где это работает
Попутешествуем мысленно по Вселенной и найдем ускорение свободного падения на планетах и других космических телах. Астронавты НАСА планируют уже в течение ближайших десятилетий высадиться на одном из астероидов. Возьмем Весту – самый большой астероид в Солнечной системе (Церера была побольше, но ее недавно перевели в разряд карликовых планет, «повысили в звании»).
g Весты = 0,22 м/с 2 .
Все массивные тела станут легче в 45 раз. При такой маленькой гравитации проблемой станут любые работы на поверхности. Неосторожный рывок или прыжок сразу подбросит астронавта на несколько десятков метров вверх. Что уж говорить про планы по добыче на астероидах полезных ископаемых. Экскаватор или бурильную установку придется в прямом смысле слова привязывать к этим космическим скалам.
А теперь другая крайность. Представим себя на поверхности нейтронной звезды (тело с массой солнца, имеющее при этом диаметр около 15 км). Так вот, если каким-то непостижимым образом астронавт не погибнет от зашкаливающего радиационного излучения всех возможных диапазонов, то его взору предстанет следующая картина:
g н.звезды = 6,67∙10 -11 ∙1,9885·10 30 / 7500 2 = 2 357 919 111 111 м/с 2 .
Монетка массой в 1 грамм весила бы на поверхности этого уникального космического объекта 240 тысяч тонн.
Источник