Как найти широту зенита солнца
Широта северного полюса Земли равна 90 o , а следовательно, отвесная линия совпадает там с осью мира, а экватор — с горизонтом. Значит, в каждый день года Солнце описывает на небосводе круги, приблизительно параллельные горизонту, на высоте, равной склонению Солнца в этот день (рис. 14). Таким образом, если бы не было рефракции, 21 марта Солнце обходило бы горизонт, причем центр Солнца лежал бы на математическом горизонте. Из-за рефракции такая картина наблюдается на несколько дней раньше. С каждым днем Солнце все увеличивает свою высоту над горизонтом, и достигает максимальной высоты 
22 июня. После этой даты высота Солнца вновь начинает уменьшаться, и вблизи 23 сентября (теперь из-за рефракции чуть позже) Солнце вновь оказывается на горизонте. В последующие дни Солнце оказывается под горизонтом и не появляется почти до дня весеннего равноденствия. Таким образом, чуть больше полугода Солнце находиться над горизонтом (полярный день), а оставшееся время — под горизонтом (полярная ночь). На южном полюсе картина такая же, только полярный день и полярная ночь меняются местами, т.е. когда на северном полюсе полярный день, на южном — полярная ночь, и наоборот.
 |
| Рис. 14. Видимое движение Солнца в течение года на полюсе Земли |
Полярные дни и ночи бывают не только на полюсах, но и на других, достаточно высоких широтах, только продолжительность их меньше. Теоретическими границами географических широт, на которых бывают полярные дни и ночи, являются северный полярный круг 
и южный полярный круг 
. Т.е. если бы Солнце было точкой и не было бы атмосферной рефракции, то на этих широтах раз в году Солнце в течение суток не заходило бы за горизонт, и в течении суток не показывалось бы над горизонтом. Из-за влияния рефракции ( 
) и конечных размеров Солнца (
) полярные дни бывают на широтах до 
, а полярные ночи лишь до широт 
. Т.е. за начало (и окончание) полярного дня мы будем брать дату, на которую наблюдаемая высота верхнего края Солнца в момент нижней кульминации равна нулю, а за начало (и окончание) полярной ночи дату, на которую наблюдаемая высота верхнего края Солнца в момент верхней кульминации равна нулю.
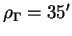
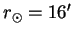
7.2. Суточное движение Солнца на экваторе.
Широта экватора равна нулю, и ось мира лежит там в плоскости горизонта, так что северный полюс мира совпадает с точкой севера, а южный — с точкой юга (рис. 15). Суточные параллели перпендикулярны горизонту, а экватор проходит через зенит (т.Q совпадает с т.Z). Таким образом, 21 марта Солнце находится на экваторе и кульминирует в зените. В последующие дни склонение Солнца увеличивается и оно кульминирует на все меньшей высоте к северу от зенита. Высота Солнца в момент верхней кульминации к северу от зенита является наименьшей 22 июня. Далее максимальная высота Солнца вновь начинает расти и 23 сентября Солнце вновь кульминирует в зените. Склонение Солнца продолжает уменьшаться и с каждым днем оно кульминирует на все меньшей высоте теперь уже к югу от зенита. Минимальная высота в верхней кульминации к югу от зенита бывает в день зимнего солнцестояния 22 декабря, а потом высота Солнца в кульминации вновь начинает увеличивается.
 |
| Рис. 15. Видимое движение Солнца в течение года на экваторе Земли |
Таким образом, в экваториальной зоне Земли нет привычной нам смены времен года, а есть два жарких (засушливых) периода вблизи равноденствий, и два перида дождей (относительно холодных) вблизи солнцестояний. Солнце дважды в год кульминирует в зените не только на экваторе, но и на околоэкваториальных широтах, вплоть до широт северного тропика 
и южного тропика 
. Северный и южный тропики определяются как географические широты, на которых Солнце один раз в году (соответственно в день весеннего и осеннего равноденствий) кульминирует в зените.
26. Определить продолжительность полярного дня в Мурманске ( 
).
1) В день начала (и окончания) полярного дня в момент нижней кульминации Солнца его наблюдаемый верхний край должен находиться на горизонте hminвк=0 o 0′, т.е.
Отсюда склонение Солнца в этот день равно:
2) В какие дни года склонение Солнца равно этой величине? Очевидно, что где-то вблизи 22 июня, одна дата — начала полярного дня — до 22 июня, а вторая — окончания полярного дня — после 22 июня. Середина полярного дня приходится на 22 июня.
3) Рассчитаем изменение склонения Солнца с этой даты до 22 июня 
.
4) За сколько дней склонение Солнца вблизи солнцестояния изменится на эту величину? 30 дней вблизи 22 июня склонение Солнца изменяется со скоростью 0 o .1 в день. За это время его склонение изменится ровно на 3 o . А в нашем случае изменение склонения больше. Значит, еще какое-то время склонение Солнца изменялось со скоростью 0 o .3 в день. Очевидно, что разность 3 o .25 — 3 o .00 = 0 o .25 была пройдена Солнцем с этой скоростью за один день. Значит, полярный день в Мурманске начался за 31 день до 22 июня (22 мая), а закончился через 31 день после 22 июня (23 июля). Полная продолжительность полярного дня в Мурманске составила 62 дня.
27. Определить продолжительность полярной ночи в Мурманске ( ).
1) В день начала (и окончания) полярной ночи в момент верхней кульминации Солнца его наблюдаемый верхний край должен находиться на горизонте hmaxвк=0 o 0′, т.е.
Отсюда склонение Солнца в этот день равно:
2) В какие дни года склонение Солнца равно этой величине? Очевидно, что где-то вблизи 22 декабря, одна дата — начала полярной ночи — до 22 декабря, а вторая — окончания полярной ночи — после 22 декабря. Середина полярной ночи приходится на 22 декабря.
3) Рассчитаем изменение склонения Солнца с этой даты до 22 декабря 
.
4) За сколько дней склонение Солнца вблизи солнцестояния изменится на эту величину? 30 дней вблизи 22 декабря склонение Солнца изменяется со скоростью 0 o .1 в день. За это время его склонение изменится ровно на 3 o . А в нашем случае изменение склонения меньше. Значит, для того, чтобы узнать, сколько дней прошло с интересующей нас даты до 22 декабря, достаточно разделить полное изменение склонения на скорость его изменения N d = 1 o .55 / 0 . 1 = 15 d .5. Значит, полярная ночь в Мурманске началась за 15.5 дней до 22 декабря (6 декабря), а закончилась через 15.5 дней после 22 декабря (6 января). Полная продолжительность полярной ночи в Мурманске составила 31 день.
28. Какого числа в г. Антананариву ( 
, о. Мадагаскар) Солнце кульминирует в зените?
Решение: Как известно, высота светила в момент верхней кульминации определяется по формуле (4). В зените высота Солнца должна быть 90 o , следовательно, в искомый день 
. Склонение Солнца равно этой величине в две даты вблизи 22 декабря. Разность 
. 30 дней вблизи 22 декабря склонение Солнца изменяется со cкоростью 0 o .1 в день, изменяясь за это время на 3 o . Оставшиеся 2 o .4 Солнце перемещается по 
со скоростью 0 o .3 в день за 
. Значит, Солнце в Антанариву кульминирует в зените за 38 дней (14 ноября) до 22 декабря, и через 38 дней (29 января) после 22 декабря.
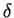
29. На одной из российских островных полярных станций полярный день длится ровно 100 дней. На какой широте расположена эта полярная станция?
30. Какова продолжительность полярного дня и полярной ночи и с какой даты по какую они длятся на широте 
?
31. Какого числа Солнце кульминирует в зените на широте 
? А на широте 
?
Источник
Зенитный угол Солнца — Solar zenith angle
Зенитный угол Солнца угла между лучами солнца и вертикальным направлением . Он тесно связан с углом солнечной высоты, который представляет собой угол между солнечными лучами и горизонтальной плоскостью. Поскольку эти два угла дополняют друг друга, косинус одного из них равен синусу другого. Оба они могут быть рассчитаны по одной и той же формуле, используя результаты сферической тригонометрии . В солнечный полдень зенитный угол минимален и равен широте минус угол склонения Солнца . Это основа, на которой древние мореплаватели путешествовали по океанам.
СОДЕРЖАНИЕ
Формула
- θ s <\ displaystyle \ theta _
>
является угол солнечного зенита - α s <\ displaystyle \ alpha _
>— угол солнечной высоты , = 90 ° — α s <\ displaystyle \ alpha _ >θ s <\ displaystyle \ theta _ > - час <\ displaystyle h>— часовой угол по местному солнечному времени .
- δ <\ displaystyle \ delta>текущее склонение Солнца
- Φ <\ displaystyle \ Phi>это местная широта .
Вывод формулы с использованием подсолнечного точечного и векторного анализа
Хотя формулу можно получить, применив закон косинуса к сферическому треугольнику зенит-полюс-Солнце, сферическая тригонометрия — относительно эзотерический предмет.
Вводя координаты подсолнечной точки и используя векторный анализ, формула может быть получена прямо без использования сферической тригонометрии.
В геоцентрической декартовой системе координат, центрированной по центру Земли ( ECEF ), пусть и будут долготой и широтой или координатами подсолнечной точки и точки наблюдателя, затем направленными вверх единичными векторами в двух точках и , находятся ( ϕ s , λ s ) <\ displaystyle (\ phi _ , \ lambda _ )> 
( ϕ о , λ о ) <\ displaystyle (\ phi _ S <\ displaystyle \ mathbf > V о z <\ displaystyle \ mathbf
S знак равно потому что ϕ s потому что λ s я + потому что ϕ s грех λ s j + грех ϕ s k <\ displaystyle \ mathbf = \ cos \ phi _ \ cos \ lambda _ <\ mathbf > + \ cos \ phi _ \ sin \ lambda _ < \ mathbf <\ mathbf , V о z знак равно потому что ϕ о потому что λ о я + потому что ϕ о грех λ о j + грех ϕ о k <\ displaystyle \ mathbf .
где , и — базисные векторы в системе координат ECEF. я <\ displaystyle <\ mathbf >> j <\ displaystyle <\ mathbf k <\ displaystyle <\ mathbf
Теперь косинус зенитного угла Солнца является просто скалярным произведением двух вышеуказанных векторов. θ s <\ displaystyle \ theta _ >
потому что θ s знак равно S ⋅ V о z знак равно грех ϕ о грех ϕ s + потому что ϕ о потому что ϕ s потому что ( λ s — λ о ) <\ displaystyle \ cos \ theta _ = \ mathbf \ cdot \ mathbf + \ cos \ phi _ \ cos (\ lambda _ — \ lambda _ .
Обратите внимание, что это то же самое , что и склонение Солнца, и эквивалентно , где — часовой угол, определенный ранее. Таким образом, приведенный выше формат математически идентичен приведенному ранее. ϕ s <\ displaystyle \ phi _ > δ <\ displaystyle \ delta> λ s — λ о <\ displaystyle \ lambda _ — \ lambda _ — час <\ displaystyle -h> час <\ displaystyle h>
Кроме того, Ref. аналогичным образом вывели формулу для азимутального угла Солнца без использования сферической тригонометрии.
Минимум и максимум
В любом заданном месте в любой заданный день зенитный угол Солнца достигает своего минимума в местный солнечный полдень, когда часовой угол , или , а именно,, или . Если это полярная ночь. θ s <\ displaystyle \ theta _ > θ м я п <\ displaystyle \ theta _ час знак равно 0 <\ displaystyle h = 0> λ s — λ о знак равно 0 <\ displaystyle \ lambda _ — \ lambda _ потому что θ м я п знак равно потому что ( | ϕ о — ϕ s | ) <\ Displaystyle \ соз \ тета _ <мин>= \ соз (| \ фи _ <о>— \ фи _ |)> θ м я п знак равно | ϕ о — ϕ s | <\ displaystyle \ theta _ |> 90^<\circ >>»> θ м я п > 90 ∘ <\ displaystyle \ theta _ 90 ^ <\ circ>>»>
И в любом месте в любой день зенитный угол Солнца достигает своего максимума в местную полночь, когда часовой угол , или , а именно,, или . Если это полярный день. θ s <\ displaystyle \ theta _ > θ м а Икс <\ displaystyle \ theta _ час знак равно — 180 ∘ <\ displaystyle h = -180 ^ <\ circ>> λ s — λ о знак равно — 180 ∘ <\ displaystyle \ lambda _ — \ lambda _ потому что θ м а Икс знак равно потому что ( 180 ∘ — | ϕ о + ϕ s | ) <\ displaystyle \ cos \ theta _ |)> θ м а Икс знак равно 180 ∘ — | ϕ о + ϕ s | <\ displaystyle \ theta _ |> θ м а Икс 90 ∘ <\ displaystyle \ theta _
Предостережения
Рассчитанные значения являются приблизительными из-за различия между общей / геодезической широтой и геоцентрической широтой . Однако эти два значения отличаются менее чем на 12 угловых минут , что меньше видимого углового радиуса Солнца.
Формула также не учитывает влияние атмосферной рефракции .
Приложения
Восход закат
Закат и восход солнца происходят (приблизительно), когда зенитный угол равен 90 °, где часовой угол h 0 удовлетворяет
потому что час 0 знак равно — загар Φ загар δ . <\ displaystyle \ cos h_ <0>= — \ tan \ Phi \ tan \ delta.>
Точное время заката и восхода происходит тогда, когда верхняя часть Солнца, преломленная атмосферой, оказывается на горизонте.
Альбедо
Средневзвешенный зенитный угол, используемый при вычислении местного альбедо Земли , определяется выражением
потому что θ s ¯ знак равно ∫ — час 0 час 0 Q потому что θ s d час ∫ — час 0 час 0 Q d час <\ displaystyle <\ overline <\ cos \ theta _ >> = <\ frac <\ int _ <- h_ <0>> ^ <\ текст
Резюме специальных углов
Например, угол возвышения Солнца равен:
- 90 °, если вы находитесь на экваторе, в день равноденствия, в двенадцатый солнечный час.
- около 0 ° на закате или на восходе
- от -90 ° до 0 ° ночью (полночь)
Дан точный расчет положения Солнца . Другие приближения существуют в другом месте.
Источник