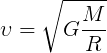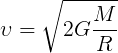Как найти первую космическую скорость для луны

Формулы и калькулятор космических скоростей

Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса. Для быстрого расчета можно воспользоваться онлайн-калькулятором.

Первая космическая скорость

Первая космическая скорость — это скорость, которую нужно придать телу, масса которого пренебрежительно мала по сравнению с массой планеты, чтобы это тело стало спутником планеты и вращалось вокруг нее по круговой траектории. Примечание: если скорость будет выше заданной (но меньше второй космической), то траектория орбиты будет не круговой, а эллипсоидной.

Формула первой космической скорости:
где G — гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10 -11 м 3 /(кг*с 2 ), или Н*м 2 /кг 2
R — радиус небесного тела
M — масса небесного тела

Вторая космическая скорость

Вторая космическая скорость — это минимальная скорость, которой должно обладать тело, чтобы преодолеть гравитационное притяжение планеты и покинуть замкнутую орбиту вокруг нее.

Формула второй космической скорости:
где G — гравитационная постоянная
R — радиус небесного тела
M — масса небесного тела

Пример:

Масса планеты Земля составляет 5,9726*10 24 кг, средний радиус — 6371 км (или 6371000 м). Подставив эти значения в формулы первой и второй космических скоростей, мы получим значение соответственно 7 910 м/с и 11 187 м/с.

Теперь рассчитаем значение космических скоростей для планеты Нептун. Масса Нептуна — 1,0243*10 26 кг. средний радиус — 24 622 км (24 622 000 м). В итоге получим значения — 16 663 м/с и 23 565 м/с.

Значения для Марса (6,4171*10 23 кг и 3389,5 км) будет 3 555 м/с и 5 027 м/с. Для Венеры (4,8675*10 24 кг и 6051,8 км) — 7 327 м/с и 10 362 м/с соответственно.

Источник

Первая космическая скорость

Первая космическая скорость – это скорость, с которой спутник движется вокруг планеты по круговой орбите, не удаляясь от планеты и не падая на нее.

То есть, для первой космической скорости орбита — это окружность. Расстояние от центра планеты до спутника равно \( R = \left( r + h \right) \). Это представлено на рисунке 1.

Формула для вычисления первой космической скорости

Первую космическую скорость можно посчитать по формуле:

\( v \left( \frac<\text<м>><\text> \right) \) (метры в секунду) – первая космическая скорость

\( M \left( \text <кг>\right) \) (килограммы) — масса планеты, вокруг которой движется спутник

\( r \left( \text <м>\right) \) (метры) – радиус планеты

\( h \left( \text <м>\right) \) (метры) — расстояние от поверхности планеты до спутника

\(G \ = 6<,>67 \cdot 10^ <-11>\left( \text <Н>\cdot \frac<\text<м>^2><\text<кг>^2> \right)\) — гравитационная постоянная

Первая космическая скорость в цифрах для некоторых небесных тел

первая космическая скорость у поверхности Земли \( v = 8000 \left( \frac<\text<м>><\text> \right) \)

первая космическая скорость у поверхности Солнца \( v = 437000 \left( \frac<\text<м>><\text> \right) \)

первая космическая скорость у поверхности Луны \( v = 1680 \left( \frac<\text<м>><\text> \right) \)

первая космическая скорость у поверхности Марса \( v = 3530 \left( \frac<\text<м>><\text> \right) \)

Как выводится формула первой космической скорости

Рассмотрим движение спутника вокруг Земли.

Земля и спутник притягиваются, запишем закон притяжения между планетой и спутником

При круговом движении на спутник действует центростремительная сила (как и на любое тело при таком движении).

Мы можем записать эти уравнения в виде системы.

\[ \begin \displaystyle F = G\cdot \frac <(r+h)^<2>> \\ \displaystyle F_<\text<ц>> = m \cdot \frac > <(r+h)>\\ \end \]

Земля и спутник притягиваются, благодаря этому спутник движется вокруг Земли по круговой орбите. Значит, притяжение между спутником и Землей – это центростремительная сила. Именно она заставляет спутник двигаться вокруг планеты по окружности. На языке математики это запишется так:

А если равны левые части уравнений, то будут равны и правые:

Масса \( m \) спутника и расстояние \( R \) между телами встречается в обеих частях уравнения. Поделим обе части уравнения на массу спутника.

Теперь умножим обе части уравнения на расстояние \(\left( r + h \right) \). Получим:

Извлечем корень квадратный из обеих частей уравнения, чтобы получить скорость:

Вам будет интересно почитать:

Движение по окружности, центростремительная сила и центростремительное ускорение

Источник

Формулы и калькулятор космических скоростей

Здесь приведены формулы и примеры расчета первой и второй космической скорости для небесных тел произвольной массы и радиуса. Для быстрого расчета можно воспользоваться онлайн-калькулятором.

Первая космическая скорость

Первая космическая скорость — это скорость, которую нужно придать телу, масса которого пренебрежительно мала по сравнению с массой планеты, чтобы это тело стало спутником планеты и вращалось вокруг нее по круговой траектории. Примечание: если скорость будет выше заданной (но меньше второй космической), то траектория орбиты будет не круговой, а эллипсоидной.

Формула первой космической скорости:
где G — гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10 -11 м 3 /(кг*с 2 ), или Н*м 2 /кг 2
R — радиус небесного тела
M — масса небесного тела

Вторая космическая скорость

Вторая космическая скорость — это минимальная скорость, которой должно обладать тело, чтобы преодолеть гравитационное притяжение планеты и покинуть замкнутую орбиту вокруг нее.

Формула второй космической скорости:
где G — гравитационная постоянная
R — радиус небесного тела
M — масса небесного тела

Пример:

Масса планеты Земля составляет 5,9726*10 24 кг, средний радиус — 6371 км (или 6371000 м). Подставив эти значения в формулы первой и второй космических скоростей, мы получим значение соответственно 7 910 м/с и 11 187 м/с.

Теперь рассчитаем значение космических скоростей для планеты Нептун. Масса Нептуна — 1,0243*10 26 кг. средний радиус — 24 622 км (24 622 000 м). В итоге получим значения — 16 663 м/с и 23 565 м/с.

Значения для Марса (6,4171*10 23 кг и 3389,5 км) будет 3 555 м/с и 5 027 м/с. Для Венеры (4,8675*10 24 кг и 6051,8 км) — 7 327 м/с и 10 362 м/с соответственно.

Источник

Как найти первую космическую скорость для луны

Найти первую и вторую космические скорости для Луны (см. условия 2.139 и 2.140).

Используя закон всемирного тяготения, находим силу притяжения Луны и тела массы m

Сила притяжения у поверхности Луны является центростремительной силой

Первая космическая скорость

Для того чтобы тело удалилось от Луны, необходимо, чтобы кинетическая энергия тела была достаточна для преодоления гравитационной потенциальной энергии, т.е.

Используя закон всемирного тяготения, находим силу притяжения Луны и тела массы m

Откуда вторая космическая скорость

Ответ:

Источник

Первая космическая скорость

Первая космическая скорость – это скорость, с которой спутник движется вокруг планеты по круговой орбите, не удаляясь от планеты и не падая на нее.

То есть, для первой космической скорости орбита — это окружность. Расстояние от центра планеты до спутника равно \( R = \left( r + h \right) \). Это представлено на рисунке 1.

Формула для вычисления первой космической скорости

Первую космическую скорость можно посчитать по формуле:

\( v \left( \frac<\text<м>><\text> \right) \) (метры в секунду) – первая космическая скорость

\( M \left( \text <кг>\right) \) (килограммы) — масса планеты, вокруг которой движется спутник

\( r \left( \text <м>\right) \) (метры) – радиус планеты

\( h \left( \text <м>\right) \) (метры) — расстояние от поверхности планеты до спутника

\(G \ = 6<,>67 \cdot 10^ <-11>\left( \text <Н>\cdot \frac<\text<м>^2><\text<кг>^2> \right)\) — гравитационная постоянная

Первая космическая скорость в цифрах для некоторых небесных тел

первая космическая скорость у поверхности Земли \( v = 8000 \left( \frac<\text<м>><\text> \right) \)

первая космическая скорость у поверхности Солнца \( v = 437000 \left( \frac<\text<м>><\text> \right) \)

первая космическая скорость у поверхности Луны \( v = 1680 \left( \frac<\text<м>><\text> \right) \)

первая космическая скорость у поверхности Марса \( v = 3530 \left( \frac<\text<м>><\text> \right) \)

Как выводится формула первой космической скорости

Рассмотрим движение спутника вокруг Земли.

Земля и спутник притягиваются, запишем закон притяжения между планетой и спутником

При круговом движении на спутник действует центростремительная сила (как и на любое тело при таком движении).

Мы можем записать эти уравнения в виде системы.

\[ \begin \displaystyle F = G\cdot \frac <(r+h)^<2>> \\ \displaystyle F_<\text<ц>> = m \cdot \frac > <(r+h)>\\ \end \]

Земля и спутник притягиваются, благодаря этому спутник движется вокруг Земли по круговой орбите. Значит, притяжение между спутником и Землей – это центростремительная сила. Именно она заставляет спутник двигаться вокруг планеты по окружности. На языке математики это запишется так:

А если равны левые части уравнений, то будут равны и правые:

Масса \( m \) спутника и расстояние \( R \) между телами встречается в обеих частях уравнения. Поделим обе части уравнения на массу спутника.

Теперь умножим обе части уравнения на расстояние \(\left( r + h \right) \). Получим:

Извлечем корень квадратный из обеих частей уравнения, чтобы получить скорость:

Вам будет интересно почитать:

Движение по окружности, центростремительная сила и центростремительное ускорение

Источник