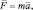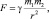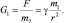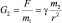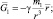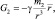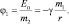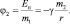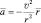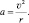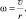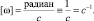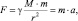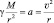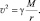Как найти напряженность гравитационного поля земли у поверхности луны

Все тела обладающие массой притягиваются друг к другу. Исаак Ньютон на основе многолетних данных астрономических наблюдений и законов динамики сформулировал закон всемирного тяготения : две любые материальные точки массами m 1 и m 2 притягиваются друг к другу вдоль линии соединяющей точки с силой прямо пропорциональной произведению масс точек и обратно пропорциональной квадрату расстояния (r) между ними:

где — гравитационная постоянная. Из формулы видно, что величина гравитационного взаимодействия не зависит от среды, в которой находятся взаимодействующие тела, гравитационное взаимодействие существует и в вакууме. На рисунке1.8.1 изображено направление сил гравитационного взаимодействия двух материальных точек.

Земля не является «материальной точкой» для тел, расположенных на ее поверхности. Теоретически доказано, что сила, с которой Земля притягивает тела, расположенные вне ее, равна силе, которую создавала бы материальная точка массой (М), равной массе Земли, и расположенная в центре Земли. Назовем силой тяжести силу, с которой тело взаимодействует с планетой, вблизи которой оно находится.

В соответствии с законом всемирного тяготения на материальную точку массой (m) со стороны Земли будет действовать сила тяжести, равная

где R — радиус Земли, в месте расположения точки. Выражение (1.8.2.) можно переписать в виде:

где g — имеет смысл ускорения, с которым движутся под действием силы тяжести все материальные тела у поверхности Земли.

Согласно фундаментальному физическому закону — обобщенному закону Галилея , все тела в одном и том же поле тяготения падают с одинаковым ускорением. Оно изменяется вблизи поверхности Земли с широтой в пределах от 9,780 м/с 2 на экваторе до 9,832 м/с 2 на полюсах. Это обусловлено суточным вращением Земли, с одной стороны, и сплюснутостью Земли — с другой (экваториальный и полярный радиусы Земли равны соответственно 6378 и 6357 км). Так как различие значений g невелико, ускорение свободного падания, которое используется при решении практических задач, принимается равным 9,81 м/с 2 .

Пусть тело расположено на расстоянии (±h) от поверхности Земли (знак плюс — над поверхностью, знак минус — под поверхностью), тогда сила тяжести с удалением от поверхности Земли уменьшается, а при приближении к центру Земли — увеличивается:

Вес тела — сила, с которой тело вследствие тяготения к Земле действует на опору или подвес, удерживающую тело от свободного падения.

Вес тела проявляется, когда тело движется с ускорением отличным от ускорения свободного падения (g), т.е. когда на тело кроме силы тяжести действуют другие силы. Если тело движется в поле тяготения Земли с ускорением , то к этому телу приложена дополнительная сила , удовлетворяющая условию:

Вес тела , движущегося с ускорением равен произведению массы тела на геометрическую разность ускорения свободного падения и ускорения тела.

Если тело движется с ускорением равным ускорению силы тяжести, то вес тела будет равен нулю:

1) вес тела равен нулю когда тело движется с ускорением равным ускорению силы тяжести ( ) в лифте вертикально вниз;

2) космический корабль движется по орбите, при этом его центростремительное ускорение , направлено так же как ускорение силы тяжести вдоль радиуса к центру Земли, и вес всех тел находящихся в корабле равен нулю.

Закон всемирного тяготения определяет величину и направление силы всемирного тяготения, но не отвечает на вопрос как осуществляется это взаимодействие. Гравитационное взаимодействие между телами осуществляется с помощью поля тяготения, или гравитационного поля.

Гравитационное поле — это особый вид материи, который создается вокруг любого тела обладающего массой, главное свойство гравитационного поля — действовать на тела, обладающие массой. Как и любое поле — гравитационное поле характеризуется с помощью двух физических величин:

1. Напряженность гравитационного поля ( ), силовая характеристика поля, равна силе, действующей со стороны поля на материальную точку единичной массы, и совпадает по направлению с действующей силой (это ничто иное как ускорение, с которым тело движется в поле тяготения):

Единица измерения напряженности гравитационного поля [g]=м/с 2 .

Линия напряженности гравитационного поля — линия, касательные, к каждой точке которой совпадает с вектором напряженности.

На всякое тело массой m, внесенное в поле, действует сила тяготения или сила тяжести , равная произведению массы тела на напряженность гравитационного поля в месте расположения тела:

Независимо от своей массы все тела под действием силы тяжести движутся с одинаковым ускорением ( )

2. Потенциал гравитационного поля (φ) — энергетическая характеристика поля, скалярная величина, определяемая потенциальной энергией тела единичной массы в данной точке поля:

Единица измерения [φ]=Дж/кг.

Потенциальная энергия тела в гравитационном поле равна:

Тогда работа гравитационного поля по перемещению тела из точки с потенциалом φ 1 в точку с потенциалом φ 2 равна:

Работа гравитационного поля по перемещению тела между двумя точками не зависит от траектории движения тела, а определяется только разностью потенциалов начальной и конечной точек, на замкнутом пути работа гравитационного поля равна нулю. То есть, сила всемирного тяготения и сила тяжести являются консервативными.

Читайте также: Луна метеорит упал 2020

Эквипотенциальные поверхности — поверхности, образованные точками поля, потенциал которых одинаков. Работа гравитационного поля при движении тела вдоль эквипотенциальной поверхности равна нулю.

Можно дать второе определение потенциала поля тяготения — это работа по перемещению единичной массы из данной точки поля в бесконечность.

В качестве примера рассмотрим гравитационное поле материальной точки.

1. Напряженность гравитационного поля материальной точки массой (M) прямо пропорциональна массе точки, и убывает по величине обратно пропорционально расстоянию от этой точки (r), направлена вдоль лучей, сходящихся в точке — источнике поля:

2. Потенциал гравитационного поля материальной точки массой (M) — прямо пропорционален массе материальной точки, создающей поле и убывает обратно пропорционально расстоянию от источника поля:

Из формулы (1.8.11) вытекает, что геометрическое место точек с одинаковым потенциалом, т.е. эквипотенциальные поверхности данного поля — это сферические поверхности.

Наглядную картину поля представляет набор линий напряженности и эквипотенциальных поверхностей, например, гравитационное поле материальной точки представлено на рисунке (1.8.2).

Потенциальная энергия тела массой (m), находящегося на расстоянии r от источника гравитационного поля — тела массой (M):

Мы уже упоминали, что гравитационное поле Земли можно рассматривать, как поле материальной точки расположенной в центре Земли. Тогда потенциальная энергия тела, находящегося на высоте h относительно Земли:

где R — радиус Земли. Так как

, и, учитывая, что h .

Потенциальная энергия тела на высоте h над поверхностью Земли, равна:

Рассмотрим взаимосвязь между потенциалом и напряженностью поля тяготения.

Элементарная работа, совершаемая полем при малом перемещении тела массой (m), равна

С другой стороны ,

где dl — элементарное перемещение.

Величина dφ/dl характеризует изменение потенциала на единицу длины в направлении перемещения в поле тяготения, это ничто иное, как градиент потенциала.

Таким образом, напряженность гравитационного поля численно равна градиенту потенциала гравитационного поля и направлена в сторону его уменьшения:

На Земле приблизительно инерциальными являются системы отсчета, которые покоятся или движутся равномерно и прямолинейно относительно точек на поверхности Земли.

Системы отсчета, движущиеся с ускорением, относительно ИСО — это неинерциальные системы отсчета. В них возникают силы инерции, которые требуют корректировки второго закона Ньютона.

Если учесть силы инерции, то второй закон Ньютона будет справедлив для любой системы отсчета : произведение массы тела на ускорение в рассматриваемой системе отсчета равно сумме всех сил, действующих на данное тело (включая и силы инерции). Силы инерции должны быть такими, чтобы вместе с силами , обусловленными воздействием тел друг на друга, они сообщали телу ускорение , каким оно обладает в неинерциальных системах отсчета:

Так как ( — ускорение тела в инерциальной системе отсчета), то

Силы инерции обусловлены ускоренным движением системы отсчета относительно измеряемой системы, рассматривают три варианта проявления этих сил.

1. Сила инерции возникает при ускоренном поступательном движении системы отсчета и направлена против вектора ускорения неинерциальной системы отсчета :

Вы испытываете на себе действие силы инерции каждый раз когда автомобиль, в котором вы находитесь, разгоняется — и вас прижимает к спинке сиденья, и наоборот, когда тормозит — вы удаляетесь от спинки сиденья. Система отсчета, связанная с автомобилем движется с ускорением, вы неподвижны в этой системе отсчета и на вас действует сила инерции направленная противоположно ускорению автомобиля.

2. Центробежная сила инерции — сила инерции, действующая на тело, покоящееся во вращающейся системе отсчета:

где ω — угловая скорость вращения неинерциальной системы отсчета; — радиус-вектор, характеризующий положение тела относительно оси вращения системы; центробежная сила направлена вдоль радиус-вектора в сторону от оси вращения системы.

Действию центробежной силы инерции подвергаются пассажиры в движущемся транспорте на поворотах; летчики при выполнении фигур высшего пилотажа; центробежные силы инерции используются во всех центробежных механизмах: насосах, сепараторах, где они достигают огромных значений. При проектировании быстро вращающихся деталей машин (роторов, винтов самолетов) принимаются специальные меры для уравновешивания центробежных сил инерции.

3. Сила Кориолиса — сила инерции, действующая на тело, поступательно движущееся со скоростью , во вращающейся с угловой скоростью системе отсчета:

равна произведению удвоенной массы тела на векторное произведение скорости поступательного движения тела относительно системы отсчета и угловой скорости вращения системы отсчета. Эта сила направлена перпендикулярно векторам скорости тела и угловой скорости вращения системы в соответствии с правилом правого винта.

Пусть шарик массой m движется с постоянной скорость ν вдоль радиуса равномерно вращающегося диска (рис.1.8.3). Если диск не вращается, то шарик движется вдоль радиуса и попадает в точку А, если же диск привести во вращение в направлении указанном стрелкой, то шарик катится по кривой ОВ, причем его скорость ν относительно диска изменяет свое направление. Это возможно, если на шарик действует сила перпендикулярная скорости ν — это и есть сила Кориолиса.

Земля представляет собой вращающуюся систему отсчета и действие силы Кориолиса объясняет ряд наблюдаемых на Земле явлений. Так, если тело движется в северном полушарии на север (рис.1.8.4), то сила Кориолиса будет направлена вправо по отношению к направлению движения, и тело отклонится на восток. Если тело движется в юг, то сила Кориолиса также направлена вправо по отношению к направлению движения, и тело отклонится на запад. Поэтому в северном полушарии наблюдается более сильное подмывание правых берегов рек; правые рельсы железнодорожных путей по движению изнашиваются быстрее, чем левые. Аналогично можно показать, что в южном полушарии сила Кориолиса, действующая на движущиеся тела, будет направлена влево по отношению к направлению движения.

Обратим еще раз внимание на то, что силы инерции вызываются не взаимодействием тел, а ускоренным движением системы отсчета, поэтому они не подчиняются третьему закону Ньютона. Два основных положения механики: 1) ускорение всегда вызывается силой; 2) сила всегда обусловлена взаимодействием между телами, в неинерциальных системах отсчета одновременно не выполняются.

Для любого из тел, находящихся в неинерциальной системе отсчета, силы инерции являются внешними; следовательно, здесь нет замкнутых систем. Это означает, что в неинерциальных системах отсчета не выполняются законы сохранения импульса, энергии и момента импульса .

Таким образом, силы инерции действуют только в неинерциальных системах отсчета, в инерциальных системах отсчета таких сил не существует.

Все тела независимо от их масс и химического состава, получают в данном гравитационном поле одинаковые ускорения. Поэтому в таком поле они движутся совершенно одинаково, если только одинаковы начальные условия. Тем же свойством обладают свободно движущиеся тела, если их движение рассматривать относительно какой-либо неинерциальной системы отсчета.

Силы инерции, действующие на тела неинерциальной системе отсчета, пропорциональны их массам и при прочих равных условиях сообщают этим телам одинаковые ускорения. Поэтому в «поле сил инерции» эти тела движутся совершенно одинаково, если только одинаковы начальные условия.

При некоторых условиях силы тяготения и силы инерции невозможно различить. Например, представьте себе груз, подвешенный на пружине в неподвижном лифте, висящем в однородном поле тяжести — на груз действует сила тяжести и он растягивает пружину.

Пусть лифт настолько удален от Земли и прочих небесных тел, что он не испытывает гравитационных воздействий. Пусть кто-то тянет за трос лифта, сообщая ему постоянное ускорение ( ). Гравитационного поля в лифте нет, но зато есть сила инерции ( ). Груз, подвешенный на пружине растянет ее, как если бы он обладал весом .

Все механические явления и движения в лифте будут в точности такими же, что и в неподвижном лифте, висящем в поле тяжести.

Никакой эксперимент, выполненный внутри лифта, не может отделить однородное поле тяготения от однородного поля сил инерции.

Аналогия между силами тяготения и силами инерции лежит в основе принципа эквивалентности гравитационных сил и сил инерции.

Принципа эквивалентности Эйнштейна: все физические явления в поле сил тяготения происходят совершенно так же, как и в соответствующем поле сил инерции, если напряженности обоих полей в соответствующих точках пространства совпадают, а прочие начальные условия для рассматриваемых тел одинаковы.

Принцип эквивалентности гравитационных сил и сил инерции можно рассматривать как принцип эквивалентности гравитационной и инерционной масс тела.

Источник

Научная электронная библиотека

§ 1.1.2. Гравитационное поле

Одной из основных количественных характеристик гравитационного поля, создаваемого массой М – источником гравитационного поля, служит его напряжённость – векторная величина (рис. 1.2), равная отношению силы гравитационного поля к массе m, испытывающей воздействие этой силы – пробной массе.

– векторная форма равенства;

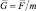
G = F/m – скалярная форма равенства.

То есть, напряжённость гравитационного поля можно воспринимать как силу этого поля, воздействующую на единицу пробной массы. В свою очередь, согласно второму закону Ньютона:

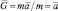
где и а – вектор ускорения и абсолютное значение ускорения пробной массы соответственно. Поэтому

Таким образом, под действием сил гравитационного поля свободная материальная точка приобретает ускорение, равное напряжённости этого поля.

Сила взаимодействия между массами подчиняется закону всемирного тяготения И. Ньютона:

Между всякими двумя материальными точками действуют силы взаимного притяжения, которые прямо пропорциональны массам точек (m1, m2) и обратно пропорциональны квадрату расстояния (r) между ними:

где γ – гравитационная постоянная (γ = 6,67∙10–11 Н∙м2/кг2).

Значит, напряжённость гравитационного поля создаваемая массой m1 может определяться равенством:

Если источником гравитационного поля является m2, то m1 – пробная масса:

или в векторной форме:

[4];

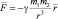
где – радиус-вектор, направленный от массы, воспринимаемой как источник гравитационного поля к пробной массе.

Потенциальная энергия взаимодействия (Еп) масс m1 и m2 определяется равенством:

[5].

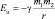
Если напряжённость – отношение силы взаимодействия к пробной массе – является силовой количественной характеристикой источника гравитационного поля, то отношение потенциальной энергии взаимодействия Еп к пробной массе m2 является энергетической количественной характеристикой источника гравитационного поля m1, и называется Ньютоновским гравитационным потенциалом (φ):

Читайте также: Почему бывают фазы луны

В случае, когда в качестве источника гравитационного поля рассматривают m2, масса m1 воспринимается как пробная:

Несмотря на то, что Земля своим гравитационным полем притягивает к себе Луну, ночное светило на Землю не падает. Это происходит потому, что Луна не покоится, а движется с постоянной скоростью вокруг Земли в направлении, перпендикулярном ускорению луны, направленном к Земле. В результате приближение Луны к Земле, вызванное ускорением , компенсируется удалением, обусловленным перпендикулярной скоростью , что и приводит к неизменности абсолютного значения расстояния между Землёй и Луной. Если приближённо считать, что луна движется вокруг Земли по строго круговой орбите, то:

или

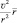
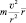
При этом, вектор называется центростремительным ускорением, а противоположный вектор называют центробежным ускорением. Соответственно, для объекта, движущегося по окружности, произведение называется центростремительной силой, а вектор, определяемый равенством – центробежной силой. Центростремительная сила гравитационного поля воздействует на пробную массу, а центробежная сила воздействует на связь между источником гравитационного поля и пробной массой. Скорость v тела, движущегося по окружности, нередко называют линейной скоростью, с тем, чтобы не путать её с угловой скоростью (), абсолютное значение которой определяется равенством

Варианты представления размерности угловой скорости, рассчитанной по приведённой формуле, выглядят следующим образом:

Скорость вращения, составляющая один оборот за секунду, в указанных единицах измерения равна 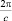. Направление угловой скорости можно определять по правилу буравчика. Поскольку, согласно закону Всемирного тяготения

где а – ускорение пробной массы m, то:

или

Таким образом, мы получили зависимость скорости вращения космического объекта от массы центра этого вращения и расстояния до него.

Вам известно, что подобно тому, как Луна вращается вокруг Земли, Земля вращается вокруг Солнца. Но и само Солнце вращается вокруг центра нашей галактики, называемой Млечный Путь. При этом, если вращение Луны вокруг Земли или Земли вокруг Солнца подчиняется последнему уравнению, то вращение Солнца вокруг центра Млечного Пути этому уравнению не подчиняется. Скорость вращения Солнца оказывается существенно большей, чем должна быть при той массе, которая наблюдается в нашей галактике. Подобное явление было обнаружено и для других звёзд, и для других галактик. То есть, оказалось, что массу галактик представляют не только звёзды, планеты, кометы и прочие наблюдаемые тела, но и материя, неизвестной природы никак не наблюдаемая. Она получила название «тёмная материя»

Тёмная материя – это неизвестное вещество, участвующее только в гравитационном взаимодействии.

Кроме того, выяснилось, что между массами, помимо сил притяжения, действуют и силы отталкивания, проявляющиеся на очень больших «космических» расстояниях. В настоящее время достоверно установлено, что Вселенная не просто расширяется, а расширяется с ускорением. То есть, расстояние между галактиками увеличивается во времени с возрастающей скоростью. Обнаруженное ускорение свидетельствует о воздействии на галактики какой-то силы, существовании Во Вселенной неизвестной ранее энергии, называемой «тёмная энергия».

Тёмная энергия – это энергия отталкивания между массами, проявляющаяся на больших «космических» расстояниях.

Примеры решения задачи

Оценить массу Земли, если известно, что её средний радиус 6371 км, а вблизи поверхности ускорение свободного падения составляет 9,8 м/c2.

;

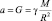
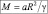
M = 9,8∙63712∙106/6,67∙10–11 ≈ 6,0∙1024 кг.

Ответ: M ≈ 6,0∙1024 кг.

Задачи для самостоятельного решения

1. Оцените абсолютное значение силы притяжения своего тела к земле, если ускорение свободного падения (g) равно 9,8 м/c2.

2. Рассчитайте силу притяжения между Землёй и луной, а также между Землёй и солнцем, если среднее расстояние до луны составляет 384 467 км, а до солнца 149,6 миллиона километров. Масса луны 7,35∙1022 кг, а масса солнца 2∙1030 кг. Оцените напряжённость гравитационного поля, создаваемого луной в точке расположения Земли и напряжённость гравитационного поля, создаваемого солнцем в этом же месте.

3. Оцените абсолютные значения:

– Ньютоновского гравитационного потенциала земли у её поверхности;

– потенциальной энергии взаимодействия Земли и своего тела.

4. Запишите в виде формулы зависимость φ от G.

5. Рассчитайте линейную скорость вращения планеты вокруг звезды, если радиус вращения составляет 1011 м, а центростремительное ускорение 2,25∙103 м/c2. Оцените абсолютное значение угловой скорости вращения этой планеты вокруг своей звезды. Выразите астрономический год этой планеты в единицах земных суток.

6. Оцените массу тёмной материи дисковидной галактики, диаметр которой составляет 9,5∙1020 м, а суммарная масса всех звёзд и планет 4,0∙1044 кг. Одна из звёзд этой галактики, расположенная от центра на расстоянии радиуса (4,75∙1020 м), вращается вокруг этого центра со скоростью 1,7∙107 м/c. С какой линейной скоростью вращалась бы эта звезда в отсутствие тёмной материи? Рассчитайте наблюдаемую работу, совершаемую силами тёмной энергии при дальнейшем удалении рассматриваемой галактики на расстояние в 1000 км от наблюдателя с ускорением 3,5∙10–24 м/c2. Ускорение считать постоянным.

1. Какие величины являются количественными характеристиками гравитационного поля?

2. Сформулируйте закон всемирного тяготения.

Источник