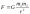Масса Солнца

Очень часто ученики не могут понять, как определили массы планет и Солнца. При этом они соглашаются с тем, что расстояния до того или иного объекта можно измерить, можно измерить и линейные размеры, но вычислить массу космических тел считают невозможным. «Их, что на весах взвешивали, что ли?» — такой вопрос приходится очень часто слышать. Так как же, происходит «взвешивание» космических объектов? Оказывается, не так уж и сложно. Ученик средней школы может сам найти массу того же Солнца.

Вот ка это делается.

Известно, что Земля вращается вокруг Солнца по орбите с радиусом около 150 млн. км. период обращения составляет 1 год, или 365 суток = 365х24х3600 секунд, что примерно составляет: 31,5 млн. секунд.

Земля на орбите удерживается благодаря гравитационным силам по закону тяготения:

Так как Земля движется по окружности, следовательно, с центростремительным ускорением. Если наша планета движется с ускорением, значит, на нее действует сила по II закону Ньютона.

Это та самая сила, с которой Солнце и наша планета взаимодействуют, т.е. сила гравитации о котрой говорилось выше. Если это одна и та же сила, то мы можем приравнять правые части уравнений:

Делим обе части на массу земли

Отсюда можно выразить массу Солнца:

Найдем теперь центростремительное ускорение , где скорость определяется как равномерная. Напомню, что при равномерном движении по окружности, скорость изменяет только свое направление.

или для движения по окружности

Теперь можно вычислить скорость, а затем ускорение и уже после сможем найти массу Солнца, но мы подставим последние 3 формулы в выражения для определения массы сОлнца и получим:

Произведем подстановку и вычисления, учитывая, что R =150 млн. км В СИ составляет 1,5 • 10 11 м, находим, что масса Солнца составляет примерно 2•10 30 кг.

Вот таким образом, имея только школьные знания в области физики и математики, можно найти массу Солнца.

Источник

Как измерить массу Земли и массу Солнца?

Простая и надежная методика измерения массы космических тел — как узнать сколько весит Солнце, зная лишь силу притяжения между космическими телами

Как можно измерить вес (точнее, массу) Солнца, если даже реальный размер нашей “домашней звезды” настолько велик, что просто не укладывается в голове? Наверняка тут должен быть какой-то секрет… И подумав так, вы будете правы и не правы одновременно.

На первый взгляд, идея измерить массу Солнца, кажется фантастикой. На самом деле для этого не понадобится ничего, кроме простейших вычислений

С одной стороны, никакого секрета в деле измерения массы любого небесного тела сколько угодно большого размера, конечно же нет. С другой стороны, без определенных хитростей тут, конечно, не обойтись.

Давайте сразу условимся – говоря, что “нам нужно определить массу Солнца”, мы имеем ввиду “определить количество вещества входящего в состав Солнца”.

Для начала измерим массу Земли

Переформулировав задачу таким образом, мы сразу же получим зацепки ведущие к решению. Первым делом нам нужно определить величину силы притяжения возникающей между любыми двумя массами.

Принцип этого определения следующий:

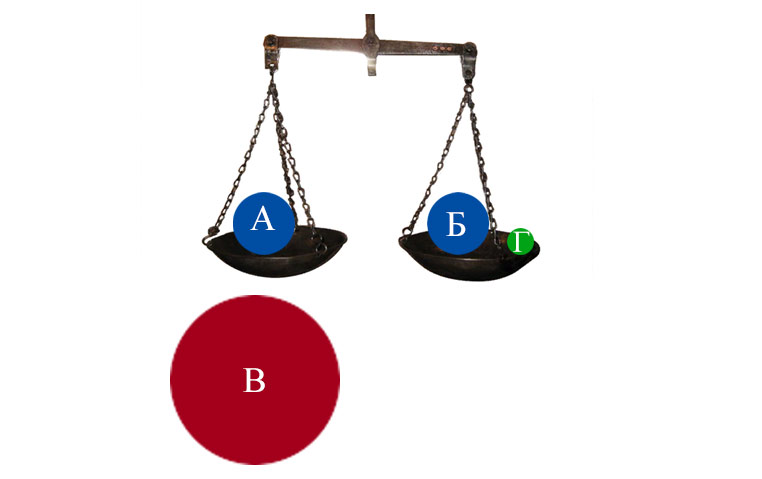
Представьте себе очень при очень чувствительные равноплечие весы с двумя чашками. В каждой чашке (А и Б) пускай лежит некий груз имеющий совершенно одинаковую массу. Весы в таком случае, будут прибывать в полном равновесии.

Теперь мы берем третье тело (В) масса которого нам также известна, и помещаем его под тело А. Взаимное притяжение между А и В, ожидаемо заставляет чашку весов А опуститься вниз. Для сохранения равновесия нам срочно необходимо добавить к массе Б очень небольшую, но опять же вполне измеримую массу Г.

Как вычислить массу планеты Земля, не выходя из дома?

Вас может заинтересовать

А вот теперь самое интересное: поскольку сила, с которой вся Земля притягивает тело Г, равна взаимному притяжению между А и В, можно без труда определить массу Земли, которая оказывается равной 6,59 х 10 21 тонн.

А теперь измерим массу Солнца!

Земля по своей орбите движется примерно так, как если бы невидимая нить соединяла ее с Солнцем. Действительно, гравитационное притяжение подобно натяжению нити, так что Земля все время движется к Солнцу, вместо того чтобы «улететь» по прямой линии, что будет, если эта “нить” вдруг оборвется. Можно сказать, что, двигаясь вокруг Солнца, Земля все время «падает» на него.

Этому “падению” соответствует отклонение ее орбиты от прямой линии, составляющее около 3 мм в секунду. Еще со времен Галилея известно, что на поверхности Земли в первую секунду своего падения всякое тело проходит 4,9 м. Расстояния 3 мм и 4,9 м прямо пропорциональны соответствующим гравитационным ускорениям, т. е. силам, действующим на единичную
массу со стороны Солнца на расстоянии Земли и Земли на ее поверхности.

Отсюда, зная, что гравитационное ускорение прямо пропорционально массе и обратно пропорционально квадрату расстояния от центра тела, можно легко вычислить, что масса Солнца в 329 390 раз больше массы Земли.

Воспользовавшись значением массы Земли, полученным выше, находим, что масса Солнца составляет 2.24 х 10 27 тонн. Полностью это немыслимое число можно записать, как 2 240 000 000 000 000 000 000 000 000 тонн.

Влияние силы тяготения на движение Земли. Путь А-С представляет собой путь пройденный Землей по орбите за 1 секунду (30 км), при этом отклонение от прямой линии B-C составит всего 3 миллиметра

Теперь уже можно вычислить и среднюю плотность Солнца, т. е. его массу, поделенную на массу воды, занимающей тот же объем.

Поскольку один кубический сантиметр воды весит один грамм, мы просто должны разделить массу Солнца (в граммах) на его объем (в кубических сантиметрах). Получим в результате число 1,42.

Иными словами, в среднем некоторый объем солнечного вещества должен весить приблизительно столько же, сколько ком битумного угля, занимающего такой же объем.

Естественно, “среднее значение” на то и среднее, чтоб представлять некую золотую середину между солнечным ядром (где плотность вещества в 10 раз превышает плотность стали) и веществом солнечной короны (где плотность падает почти до величины космического вакуума). Тем не менее, в общем и целом данная методика расчетов абсолютно верна и может с успехом применяться при расчете массы любого небесного тела – хоть астероида, хоть звезды.

Источник

Как ученые посчитали массу Солнца?

На любое тело действуют две силы или две «скорости» — сила тяготения (маленький объект падает на большой) и, собственно, скорость, с которой этот объект летит «прямо».

Первая картинка из гугла с какой-то там задачи вполне подходит для пояснения.

Если скорость большая — то тело совершает дугу и улетает. Как делают кометы.

То есть, вот она летела-летела, начала притягиваться, но поскольку летела слишком быстро, не успела упасть, а сделала дугу и улетела дальше.

Если сила тяготения большая — то тело просто падает.

А вот если оно летает по кругу — значит, эти две силы равны между собой. Земля пытается улететь, но её по чуть-чуть притягивает к себе Солнце, постоянно изменяя её траекторию вплоть до замкнутого состояния.

Центростремительная сила вычисляется по формуле F=ma. Где массу Земли мы знаем (вычислили по ходу развития науки), а ускорение — вычисляется из того, что Земля делает один оборот за год.

И, как я уже объяснил выше, эта сила должна быть равна силе тяготения. Ну а тяготение рассчитывается исходя из массы двух тел. И зная массу Земли, расстояние до Солнца, и силу, которая на Землю действует, мы спокойно можем вычислить массу Солнца.

Для расчёта в наше время хватает буквально школьного уровня знаний.

По примерно такой же методике вычисляется и масса любых других объектов — спутников, вращающихся вокруг планеты, других планет, вращающихся вокруг звёзд, самих звёзд, взаимодействующих друг с другом и так далее.

Источник

Как ученые измерили массу Земли и других планет?

Планета – объект большой, его на весы не поставишь. Как же ученым удалось узнать массу Земли? Как измеряется масса далеких космических объектов?

Занимательная физика

Существует 2 способа определения массы Земли: с помощью барометра и математических вычислений, или анализа частиц нейтрино.

Барометр и законы Ньютона

Метод, применяемый с XVIII века. Для расчета используются второй закон Ньютона (F=mg) и закон всемирного тяготения (F=G*m*M/R^2).

F – это сила земного притяжения барометра, G – коэффициент гравитационной постоянной, R – радиус планеты, m – вес прибора, M – вес планеты.

Отдельно масса Земли вычисляется по формуле: M = g*R^2/G, где g – это ускорение свободного падения.

Ускорение свободного падения узнали, сбросив барометр с высокой башни и измерив время, которое он пролетел до столкновения с землей. Выяснилось, что за каждую последующую секунду барометр преодолевал почти 9.8 метров. Таким образом, g = 9.8 м/с².

Радиус Земли был известен еще с Античности. Столь сенсационное открытие сделал греческий математик Эратосфен в III веке до н.э.

Ученый подождал день летнего солнцестояния. В это время светило находится в самой высокой точке на небе и в 12 часов отбрасывает наименьшую тень в году.

Математик присмотрелся к обелиску, стоящему неподалеку, измерил отбрасываемую им тень, измерил сам обелиск, высчитал все углы, а потом сделал то же самое в соседнем городе. Расчеты дали ему окружность земли в 38.5 тысяч километров. Современные ученые пересчитали окружность подобным методом и высчитали 40 000 км.

Планета идеальным шаром не является, а потому ее радиус оказался 6371 км.

Труднее всего было найти коэффициент гравитационной постоянной. Для этого исследователи взяли однотонный свинцовый шар и посмотрели, с какой силой он притягивал барометр.

G = 6,67430(15)*10ˆ(-11) Н·м²·кг²

Подставив все эти цифры в уравнение, ученые высчитали, что Земля весит шесть септиллионов кг или 6^24 кг .

Это мельчайшие субатомные частицы, которые испускает Солнце. Они проходят планету насквозь.

Испанские физики поставили лабораторию на Южном полюсе, дождались момента, когда Солнце окажется на Северном полюсе и выловили нейтрино с обратной стороны.

Эксперимент кажется фантастичным, однако измерив скорость частиц, прошедших сквозь Землю, физики нашли плотность планеты и, соответственно, массу.

Как измеряются далекие планеты?

Масса далеких планет вычисляется примерно. Основами для вычислений становятся орбиты планет, орбиты их спутников и гравитационные возмущения между ними.

Масса звезд вычисляется по степени их яркости. Считается, чем ярче небесное тело, тем оно массивнее. По светимости звезды определяется её химический состав, а значит примерная плотность и вес.

Источник

Как измеряют массу планет

Характеристики планет Солнечной системы были известны еще в средневековье, во времена Кеплера и Галилея. То есть, массу планет приблизительно можно было определить даже простыми методами и инструментами. В современной астрономии есть несколько методов расчета характеристик планет, звезд, скоплений и галактик.

Планеты солнечной системы

Интересный факт: 99,9% всей массы Солнечной системы сосредоточена в самом Солнце. На все планеты вместе взятые приходится не более 0,01%. При этом из этих 0,01%, в свою очередь, 99% массы приходится на газовые гиганты (в том числе 90% только на Юпитер и Сатурн).

Рассчитываем массу Земли и Луны

Чтобы измерить массу планет солнечной системы, проще всего в первую очередь найти значения для Земли. Как мы помним, ускорение свободного падения определяется по формуле F=mg, где m – масса тела, а F – действующая на него сила.

Параллельно вспоминаем универсальный закон всемирного тяготения Ньютона:

Сопоставив эти две формулы, и зная значение гравитационной постоянной 6,67430(15)·10−11 м³/(кг·с²), можно рассчитать массу Земли. Ускорение свободного падения на Земле мы знаем, 9,8 м/с2, радиус планеты тоже. Подставив все данные на выходе получим приблизительно 5,97 х 10²⁴ кг.

Зная массу Земли, мы легко рассчитает параметры по другим объектам Солнечной системы – Луна, планеты, Солнце и так далее. С Луной вообще все довольно просто. Здесь достаточно учесть, что расстояния от центров тел до центра масс соотносятся обратно их массам. Подставив эти цифры для Земли и ее спутника получим массу Луны 7.36 × 10²² килограмма.

Перейдем теперь к методикам измерения массы планет земной группы – Меркурий, Венера, Марс. После чего рассмотрим газовые гиганты, и в самом конце – экзопланеты, звезды и галактики.

Общие методики определения масс планет

Наиболее классический способ, как узнать массу планет – расчет при помощи формул третьего закона Кеплера. Он гласит, что квадраты периодов обращения планет соотносятся так же, как кубы больших полуосей орбит. Ньютон немного уточнил этот закон, внеся в формулу массы небесных тел. На выходе получилась такая формула –

Таким способом можно найти массу всех планет Солнечной системы и самого Солнца.И периоды обращения, и большие полуоси орбит планет Солнечной системы легко измеряются астрономическими методиками, доступными даже без сложных инструментов. А так как массу Земли мы уже рассчитали, можно все цифры подставить в формулу и найти конечный результат.
‘ alt=»yH5BAEAAAAALAAAAAABAAEAAAIBRAA7 — Как измеряют массу планет» title=»Как измеряют массу планет»>

В отношении же экзопланет и других звезд (но только двойных) в астрономии обычно применяется метод анализа видимых возмущений и колебаний. Он основан на том факте, что все массивные тела “возмущают” орбиты друг друга.

Такими расчетами были открыты планеты Нептун и Плутон, еще до их визуального обнаружения, как говорят “на кончике пера”.

Значения масс планет Солнечной системы

Итак, мы разобрались с общими методиками расчета масс разных небесных тел и посчитали значения для Луны, Земли и Галактики. Давайте теперь составим рейтинг планет нашей системы по их массе.

Возглавляет рейтинг с наибольшей массой планет Солнечной системы – Юпитер, которому не хватило одного порядка чтобы наша система стала двойной. Еще чуть-чуть и у нас могло быть два Солнца, второе вместо Юпитера. Итак, масса этого газового гиганта равняется 1,9 × 10²⁷ кг.

Интересно, что Юпитер – единственная планета нашей системы, центр масс вращения с Солнцем которой расположен вне поверхности звезды. Он отстоит примерно на 7% расстояния между ними от поверхности Солнца.

Вторая по массе планета – Сатурн, его масса 5,7 × 10²⁶ кг. Следующим идет Нептун – 1 × 10²⁶. Четвёртая по массе планета, газовый гигант Уран, масса которого – 8,7 × 10²⁵ кг.

Далее идут планеты земной группы, каменистые тела, в отличие от газовых гигантов с их большим радиусом и относительно малой плотностью.

Самой тяжелой из этой группы является наша планета, ее массу мы уже рассчитали. Далее идет Венера, масса этой планеты равняется 4,9 × 10²⁴ кг. После нее в рейтинге идет Марс, он почти в 10 раз легче – 6,4 × 10²³кг. И замыкает его, как планета самой маленькой массы, Меркурий – 3,3 × 10²³кг. Что интересно, Меркурий даже легче, чем два спутника в Солнечной системе – Ганимед и Каллисто.

Определение масс звезд и галактик

Для того чтобы найти характеристики одинарных звездных систем применяется гравиметрический метод. Его суть в измерении гравитационного красного смещения света звезды. Оно измеряется по формуле ∆V=0,635 M/R, где M и R – масса и радиус звезды, соответственно.

Косвенно можно также вычислить массу звезды по видимому спектру и светимости. Сначала определяется ее класс светимости по диаграмме Герцшпрунга-Рассела, а потом вычисляется зависимость масса/светимость. Такой способ не подходит для белых карликов и нейтронных звезд.

Масса галактик вычисляется в основном по скорости вращения ее звезд (или просто по относительной скорости звезд, если это не спиральная галактика). Все тот же всемирный закон тяготения Ньютона нам гласит, что центробежную силу звезд в галактике можно выразить в формуле:

Только в этот раз в формулу мы подставляем расстояние от Солнца до центра нашей галактики и его массу. Так можно рассчитать массу Млечного Пути, которая равняется 2,2 × 10⁴⁴г.

Не забываем, что эта цифра – это масса галактики без учета звезд, орбиты которых располагаются вне орбиты вращения Солнца. Поэтому для более точных расчетов берутся самые внешние звезды рукавов спиральных галактик.

Для эллиптических галактик способ нахождения массы схож, только там берется зависимость между угловым размером, скоростью движения звезд и общей массой.

Похожие статьи

Понравилась запись? Расскажи о ней друзьям!

Источник