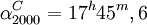Как найти часовой угол солнца

Расчет кажущегося положения Солнца

Теперь можно рассчитать кажущееся положение Солнца: высотаh и азимут А — в любой точке на широте φ в любое время суток в соответствии с углом τ и в любое время года в соответствии с углом склонения δ.

Мы же приведем результат в простейшем виде:

(3.4)

(3.5)

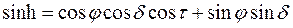
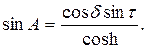
где φ — географическая широта ;

— склонение Солнца определяется по формуле ;

, град -часовой угол;

, (3.6)

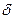
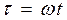
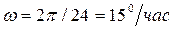
где 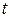— солнечное время в часах, отсчитываемое от астрономического полудня.

Очевидно, в полдень высота Солнца h максимальна, h = 90° -φ +δ.

Во время летнего солнцестояния высота Солнца в нашей местности в момент кульминации составляет: h = 90˚- φ + δ_☼ = 90˚ — 56,5˚ +23,5˚=57˚, во время зимнего солнцестояния h = 90˚- φ + δ_☼= 90˚ — 56,5˚ — 23,5˚=10˚, а в дни равноденствий, когда Солнце находится на небесном экваторе- δ_☼=0, h = 33,5˚.

Часовой угол захода(восхода) Солнца

При восходе и заходе Солнца h = 0. Из уравнения (3.4) видно, что это произойдет при углах τ в каждом из двух случаев, близких к полудню, для которых при h = 0 из уравнение имеем:

(3.7)

(3.8)

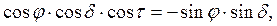
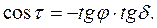
Тогда часовой угол захода (восхода) Солнца для горизонтальной поверхности

τ=arccos(-tg 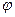tg ) (3.9)

ЛЕКЦИЯ 5

Тема: Фотоэлектрические преобразование солнечной энергии

Источник

Часовой угол

Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, система небесных координат является сферической системой координат, в которой третья координата — расстояние — часто неизвестна и не играет роли.

Системы небесных координат отличаются друг от друга выбором основной плоскости и началом отсчёта. В зависимости от стоя́щей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальные системы координат. Реже — эклиптическая, галактическая и другие.

Содержание

Горизонтальная система координат

В этой системе основной плоскостью является плоскость математического горизонта. Одной координатой при этом является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A.

Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.

Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.

Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии азимуты отсчитываются от точки севера.)

Первая экваториальная система координат

В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.

Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.

Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.

Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с небесным меридианом) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0 h до 24 h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0 h до +12 h ) к западу и от 0° до −180° (от 0 h до −12 h ) к востоку.

Вторая экваториальная система координат

В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение β (реже — полярное расстояние p). Другой координатой является прямое восхождение α.

Прямым восхождением (RA,α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0 h до 24 h (в часовой мере).

RA — астрономический эквивалент земной долготы. И RA и долгота измеряют угол восток-запад вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Для долготы, нулевой пункт — нулевой меридиан; для RA нулевой отметкой является место на небе, где Солнце пересекает небесный экватор в весеннее равноденствие.

Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу.

Объект на небесном экваторе имеет склонение 0°
Склонение северного полюса небесной сферы равно +90°
Склонение южного −90°

У склонения всегда указывается знак, даже если склонение положительно.

Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную отрицательной). В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > 90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ [1]

Эклиптическая система координат

В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.

Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики.

Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть к востоку от точки весеннего равноденствия в пределах от 0° до 360°.

Галактическая система координат

В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.

Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило.

Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до −90° к южному галактическому полюсу.

Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.

Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).

Координаты точки начала отсчёта C на эпоху 2000 в экваториальной системе координат составляют:

Изменения координат при вращении небесной сферы

Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.

История и применение

Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат.

Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.

Использование различных систем координат

Горизонтальная система координат используется для определения направления на светило с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке.

Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке.

Вторая экваториальная система координат является общепринятой в астрометрии. В этой системе составляются звёздные карты и описываются положения светил в каталогах.

Эклиптическая система координат используется в теоретической астрономии при определении орбит небесных тел.

Источник

1 Годовое движение Солнца и эклиптическая система координат

Солнце наряду с суточным вращением медленно в течение года перемещается по небесной сфере в противоположном направлении по большому кругу, называется эклиптикой. Эклиптика наклонена к небесному экватору под углом Ƹ, Величина которого в настоящее время близка к 23 26´. Эклиптика пересекается с небесным экватором в точке весеннего ♈ (21 марта) и осеннего Ω (23 сентября) равноденствий. Точки эклиптики, отстоящие от равноденственных на 90 , есть точки летнего (22 июня) и зимнего (22 декабря) солнцестояний. Экваториальные координаты центра солнечного диска непрерывно изменяются в течении года от 0h до 24 h (прямое восхождение) – эклиптическая долгота ϒm, отсчитывается от точки весеннего равноденствия до круга широты. И от 23 26´ до -23 26´ (склонение) – эклиптическая широта, отсчитывается от 0 до +90 к северному полюсу и 0 до -90 к южному полюсу. Зодиакальными созвездиями называются созвездия, которые находятся на линии эклиптики. Находится на линии эклиптики 13 созвездий: Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Козерог, Водолей, Рыбы и Змееносец. Но созвездие Змееносца не упоминается, хотя Солнце и находится в нём большую часть времени созвездий Стрельца и Скорпиона. Сделано это для удобства. При нахождении Солнца под горизонтом на высотах от 0 до -6 — длятся гражданские сумерки, а от -6 до -18 — астрономические сумерки.

2 Измерение времени

Измерение времени основано на наблюдениях суточного вращения свода и годичного движения Солнца, т.е. вращения Земли вокруг своей оси и на обращении Земли вокруг Солнца.

Продолжительность основной единицы времени, называемой сутками, зависит от избранной точки на небе. В астрономии за такие точки принимаются:

— Точка весеннего равноденствия ♈ (звёздное время);

— Центр видимого диска Солнца (истинное Солнце, истинное солнечное время);

— среднее Солнце – фиктивная точка, положение которой на небе может быть вычислено теоретически для любого момента времени (среднее солнечное время)

Для измерения длинных промежутков времени служит тропический год, основанный на движении Земли вокруг Солнца.

Тропический год – промежуток времени, между двумя последовательными прохождениями центра истинного центра Солнца через точку весеннего равноденствия. Он содержит 365,2422 средних солнечных суток.

Из-за медленного движения точки весеннего равноденствия навстречу Солнцу, вызванного прецессией, относительно звёзд Солнце оказывается в той же точке неба через промежуток времени на 20 мин. 24 сек. больший, чем тропический год. Он называется звёздным годом и содержит 365,2564 средних солнечных суток.

3 Звёздное время

Промежуток времени между двумя последовательными кульминациями точки весеннего равноденствия на одном и том же географическом меридиане называется звёздными сутками.

Звёздное время измеряется часовым углом точки весеннего равноденствия: S=t_♈, и равно сумме прямого восхождения и часового угла любой звезды: S = α + t.

Звёздное время в любой момент равно прямому восхождению какого — либо светила плюс его часовой угол.

В момент верхней кульминации светила его часовой угол t=0, а S = α.

4 Истинное солнечное время

Промежуток времени между двумя последовательными кульминациями Солнца (центра солнечного диска) на одном и том же географическом меридиане называется истинными солнечными сутками.

За начало истинных Солнечных суток на данном меридиане принимают момент нижней кульминации Солнца (истинная полночь).

Время, протекающее от нижней кульминации Солнца до любого другого его положения, выраженное в долях истинных солнечных суток называется истинным солнечным временем Т_ʘ

Истинное солнечное время выражается через часовой угол Солнца, увеличенный на 12 часов: Т_ʘ = t_ʘ + 12 h

5 Среднее солнечное время

Для того, чтобы сутки имели постоянную продолжительность и при этом были связаны с движением Солнца, в астрономии введены понятия двух фиктивных точек:

— средне эклиптического и средне экваториального Солнца.

— Среднее эклиптическое Солнце (ср.эклип.С.) равномерно движется по эклиптике со средней скоростью.

— Среднее экваториальное Солнце движется по экватору с постоянной скоростью среднего эклиптического Солнца и одновременно с ним проходит точку весеннего равноденствия.

Промежуток времени между двумя последовательными кульминациями среднего экваториального Солнца на одном и том же географическом меридиане, называется средними солнечными сутками.

Время, протекающее от нижней кульминации среднего экваториального Солнца до любого другого его положения, выраженное в долях средних солнечных суток называется средним солнечным временем Т_m.

Средне солнечное время Т_m на данном меридиане в любой момент численно равно часовому углу Солнца: Т_m = t_m + 12 h

6 Всемирное, поясное и декретное время

Местное среднее солнечное время гринвичского меридиана называется всемирным или мировым временем Т₀_.

Местное среднее солнечное время любого пункта на Земле определяется: Т_m= Т₀ + λ h

Счёт времени ведётся на 24 основных географических меридиана, расположенных друг от друга на долготе точно через 15 (или 1 час) приблизительно посредине каждого часового пояса. Основным нулевым меридианом считается гринвичский. Поясное время есть всемирное время плюс номер часового пояса: Т_П= Т₀ + n

В России в практической жизни до марта 2011 г. использовалось декретное время:

Декретное время второго часового пояса, в котором располагается Москва, называют московским временем. В летний период (апрель-октябрь) стрелки часов переводились на час вперёд, а в зимний возвращались на час назад.

7 Рефракция

Видимое положение светил над горизонтом отличается от вычисленного по формулам. Лучи от небесного объекта, прежде чем попасть в глаз наблюдателя, проходят сквозь атмосферу Земли и преломляются в ней. И так ка плотность увеличивается к поверхности Земли, то луч света всё более отклоняется в одну и ту же сторону по кривой линии, так что направление ОМ₁, по которому наблюдатель видит светило, оказывается отклонённым в сторону зенита и не совпадает с направлением ОМ₂, по которому бы он видел светило при отсутствии атмосферы.

Явление преломления световых лучей при прохождении земной атмосферы называется астрономической рефракцией. Угол М₁ОМ₂ называют углом рефракции или рефракцией ρ.

Угол ZOM₁ называется видимым зенитным расстоянием светила zʹ, а угол ZOM₂ – истинным зенитным расстоянием z: z — zʹ = ρ, т.е. истинное расстояние светила больше видимого на величину ρ.

На линии горизонта рефракция в среднем равна 35ʹ.

Вследствие рефракции наблюдаются изменения формы дисков Солнца и Луны при их восходе или заходе.

Источник