Законы движения планет
В начале 17 века немецкий математик и астроном Иоганн Кеплер вывел три закона движения планет в Солнечной системе. Они были выведены на основании наблюдений за небесными телами, сделанных Браге и другими исследователями космического пространства того времени.
Первый закон Кеплера
Кеплер обратил внимание, что результаты наблюдений Браге расходятся с представлениями о круговой траектории обращения планет вокруг Солнца. Особенно это касалось Марса, чья траектория движения по наблюдения датчанина никак не могла описывать идеальный круг. Браге был очень точен в своих расчетах и сомнений в их правдивости у его последователя не возникло.
Тогда немецкий математик принял орбиты за эллипсы, у каждого из которых есть два фокуса. Это условные точки, выбранные таким образом, что сумма расстояний от них до любой точки эллипса – величина постоянная. При этом для эллиптической орбиты в одном из фокусов находится Солнце.
Форма эллипса вычисляется благодаря отношению фокального расстояния к большой полуоси орбиты. Полученное значение описывает эксцентриситет орбиты. Если он равен нулю – орбита представляет собой идеальную окружность, от нуля до единицы – эллипс различной вытянутости, больше единицы – параболу.
Второй закон Кеплера
Если орбита – это эллипс, то каким образом происходит движение небесного тела по ней? В каких отрезках орбитального пути оно ускоряется и замедляется?
Немецкий ученый обнаружил, что есть взять два любых отрезка орбитального пути, которые планета Солнечной системы проходит за одинаковые промежутки времени, провести от их концов радиус-векторы к центральной звезде, то площади полученных образований будут одинаковы. Это упрощенная формулировка второго закона.
Для того, чтобы постоянство площадей сохранялось, тело должна двигаться в разных точках орбиты с разной скоростью. Так, например, Земля в наибольшем приближении к Солнцу движется быстрее, чем в максимальном удалении от него
Третий закон Кеплера
Третий постулат о движении небесных тел в Солнечной системе как раз касается понятий перигелия и афелия. Если провести между ними условную линию, получится большая ось траектории обращения планеты. Соответственно, половина этого отрезка – большая полуось.
Кеплер на основании наблюдений вывел, что отношение полных оборотов вокруг центральной звезды для двух любых планет системы, возведенных в квадрат, всегда равняется отношению больших полуосей орбитальных путей этих тел, возведенных в куб.
Трудность в доказательстве и принятии трех законов состояла в том, что он вывел их эмпирически. Но в конце 17 века Ньютоном был открыта классическая теория тяготения. Он и помог установить правильность суждений немецкого астронома и описал движение планет по эллипсу вокруг Солнца. Ньютон установил, что кроме массы объекта и его удаления от звезды никакие другие свойства не влияют на гравитационное притяжение.
Также Ньютон внес корректировки и в третий постулат Кеплера. Он открыл, что для соблюдения соотношения необходимо учитывать массу космического объекта. Данная трактовка третьего закона помогает установить массу планеты или спутника, зная величину его орбиты и период обращения.
Законы Иоганна Кеплера помогли установить форму планетарной траектории, вычислить период обращения планет, их скорость и ее изменения по мере приближения и удаления от Солнца. Ученый вывел Землю из ранга особенных астрономических объектов системы и установил, что она подчиняется всем трем законом, как и любая другая планета нашей звездной системы.
Источник
Движение планет вокруг Солнца
Главным образом, движение планет Солнечной системы имеет два направления. Во-первых, происходит вращение планет вокруг Солнца. Во-вторых, одновременно с ним они обращаются вокруг галактического центра.

В глубокой древности верили, что наша планета является центром всего мира. Но со временем люди узнали, что это не так.
Согласно гелиоцентрической системе мира, созданной Николаем Коперником, все планетные тела, в том числе и Земля, совершают оборот по орбитам вокруг Солнца.
Затем большой вклад в развитие астрономии внёс Тихо Браге, наблюдавший за небесными телами.
На основании полученных им результатов, математик Иоганн Кеплер вывел свои знаменитые законы. К тому же, Ньютоном был открыт закон всемирного тяготения. Собственно говоря, эти знания значительно повлияли на представление об эллиптических орбитах космических объектов.

Законы движения планет Иоганна Кеплера
Как известно, всего есть три основных постулата астронома для каждой планеты:
- Она совершает обороты по эллипсу, в одном из фокусов которого находится Солнце.
- Небесное тело осуществляет движение в плоскости, которая проходит сквозь солнечный центр. Причем радиус — вектор, соединяющий планету и Солнце, за одинаковые промежутки времени заметает собой равные площади.
- Квадраты периодов обращения планет вокруг Солнца относятся как кубы больших полуосей орбит планет. Что, соответственно, позволяет вычислить скорость планеты и промежуток времени, затрачиваемый на полный оборот вокруг Солнца.
Что важно, периоды обращения по окружности главного светила у каждого планетного тела индивидуальный. Например, Земля совершает его за 365 дней (год), хотя Меркурию на это требуется всего 88 земных дней. В то же время, Юпитер затрачивает 11,9 лет, а Плутон вообще 247,7 лет.
Вдобавок, при этом каждая отдельная планета вращается вокруг своей оси также со своей скоростью.

Движение нижних планет
По характеру перемещения и положения к земной орбите различают нижние или внутренние (Меркурий, Венера) и верхние или внешние (все оставшиеся) планеты.
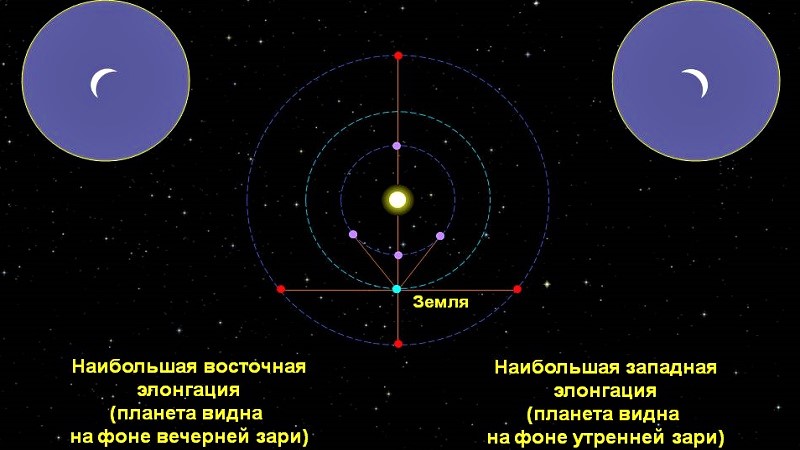
Между прочим, нижние движутся недалеко от Солнца, и могут располагаться на востоке или западе от него.
Существует, так называемая, элонгация, то есть максимальная угловая отдалённость от центрального светила. Когда планета имеет наибольшую удалённость к востоку — это восточная (вечерняя) элонгация, а к западу — это уже западная (утренняя) элонгация.
Движение планет в направлении с востока на запад называется попятным. При нём происходит сближение с Солнцем. Однако добираясь к западной элонгации, небесное тело замирает и начинает двигаться в обратную сторону. Такое перемещение, как бы догоняющее Солнце, называют прямым.
Собственно, достигнув его, планета оказывается невидимой — верхнее соединение. Проще говоря, в это время между ней и Землёй лежит Солнце, которое закрывает обзор.
Затем небесное тело снова добирается до момента восточной элонгации, опять останавливается и пускается в попятное движение. Таким образом цикл возобновляется.
Движение верхних планет
На самом деле, оно осуществляется по аналогии с внутренними объектами нашей системы. У них соответственно сменяется прямое и попятное перемещение по небесной сфере. Во время нахождения на западе вслед за солнечным заходом, они двигаются прямо, так же как и Солнце. Правда, скорость движения внешних планет меньше его. Но догнав светило — соединяется с ним. После чего, Солнце обгоняет планетный объект и мы наблюдаем его на востоке.
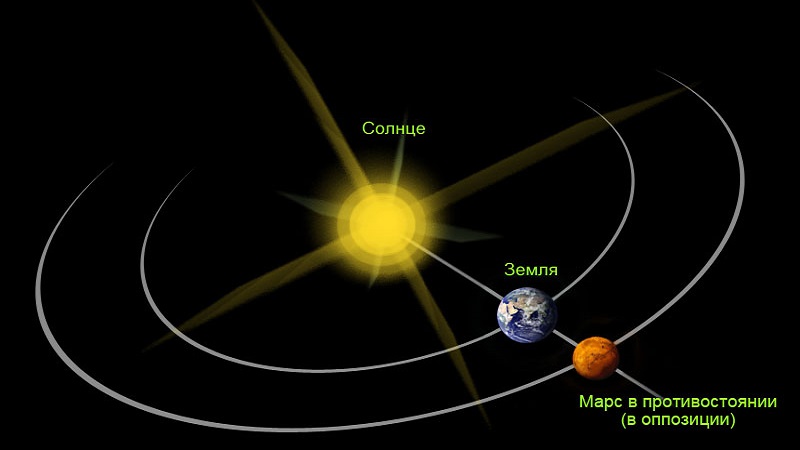
Как итог, планета замедляется и останавливается, а потом начинается попятный процесс. В какой-то момент она попадает в точку на небе, противоположную солнечному расположению. К слову, это называют противостоянием. То есть в это время между центральной звездой и планетой находится Земля.
Между тем, спустя некоторый промежуток времени планета останавливается и вновь меняет своё направление. В принципе, цикл повторяется.
Стоит отметить, что положения планетных тел никак не связаны с земным суточным вращением.
Конечно, очень любопытно как небесные тела взаимодействуют между собой, как они перемещаются. Вообще всё, что с ними связано вызывает интерес. Прежде всего потому что наша Земля принимает непосредственное участие в этом. Она также подчиняется законам Вселенной, которые люди пытаются постичь.главное слово-движение планет.
Источник
Как изменяется периоды обращения планет вокруг солнца
Цель работы: изучение движения тел под действием сил тяготения; проверка третьего закона Кеплера.
На смену геоцентрической системе мира, созданной в начале нашей эры Птолемеем, пришла гелиоцентрическая система, созданная Коперником. Несколько позднее немецкий астроном И. Кеплер на основе астрономических наблюдений установил законы движения планет вокруг Солнца.
Согласно 1-му закону Кеплера любая планета движется вокруг Солнца по замкнутой кривой, которая называется эллипсом (внешне похож на овал). Солнце находится в одном из фокусов этого эллипса. Эллипс имеет два фокуса: это две такие точки внутри кривой, сумма расстояний от которых до произвольной точки эллипса постоянна. Оказывается, что орбиты всех планет Солнечной системы лежат примерно в одной плоскости. Большинство планет движутся по орбитам-эллипсам, которые близки к окружностям. Лишь Марс и Плутон имеют сравнительно вытянутые орбиты.
Второй закон Кеплера устанавливает, что скорость планеты больше тогда, когда она в своем движении находится ближе к Солнцу (в так называемой точке перигелия) и меньше тогда, когда она находится на наибольшем расстоянии от Солнца (в точке афелия). Третий закон Кеплера устанавливает связь между периодом обращения планеты вокруг Солнца и ее средним расстоянием от Солнца, он применяется ко всему коллективу планет Солнечной системы.
Законы Кеплера получили свое объяснение лишь после открытия законов тяготения. Физические объекты участвуют в гравитационном взаимодействии, т.е. они притягиваются друг к другу. Гравитационное взаимодействие обладает всеобщей универсальностью: ему подвержены все материальные объекты и даже физические поля. Закон всемирного тяготения был открыт И. Ньютоном. Он утверждает, что два неподвижных точечных тела взаимодействуют друг с другом с силой, пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними, т.е.
 , , | (1) |
где γ называют гравитационной постоянной. Этот закон справедлив и для взаимодействия однородных шаров, но в этом случае под r следует понимать расстояние между их центрами.

Отсюда получаем, что 


Это и есть третий закон Кеплера, который можно сформулировать следующим образом: отношение куба расстояния от планеты до Солнца к квадрату периода ее обращения вокруг Солнца есть величина постоянная, одинаковая для всех планет Солнечной системы. В случае движения по эллипсу, когда расстояние от планеты до Солнца при движении изменяется, в законе фигурирует некоторое среднее расстояние, т.е. полусумма максимального и минимального расстояний от данной планеты до Солнца. Закон Кеплера справедлив для любой планетной системы, а также для системы спутников какой-либо конкретной планеты, например, для системы спутников Юпитера или Урана. В последнем случае под М в формуле (2) понимается масса соответственно Юпитера или Урана.
Источник
§ 4. Законы движения планет
Изучив этот параграф, мы узнаем:
- что планеты в Солнечной системе движутся согласно законам Кеплера;
- о законе всемирного тяготения, который управляет движением всех космических тел — от планет до галактик.
| Конфигурациями планет называют характерные взаимные положения планет относительно Земли и Солнца |
Конфигурации планет
Конфигурации планет определяют расположение планет относительно Земли и Солнца и обусловливают их видимость на небе. Все планеты светятся отраженным солнечным светом, поэтому лучше всего видна та планета, которая находится ближе к Земле, при условии, если к нам повернуто ее дневное, освещенное Солнцем полушарие.
На рис. 4.1 изображено противостояние (ПС) Марса (М1), то есть такая конфигурация, когда Земля находится на одной прямой между Марсом и Солнцем. В противостоянии яркость планеты самая большая, потому что к Земле обращено все ее дневное полушарие.
Орбиты двух планет, Меркурия и Венеры, расположены ближе к Солнцу, чем Земля, поэтому в противостоянии они не бывают. В положении, когда Венера или Меркурий находятся ближе всего к Земле, их не видно, потому что к нам повернуто ночное полушарие планеты (рис. 4.1). Такая конфигурация называется нижним соединением с Солнцем В верхнем соединении планету тоже не видно, потому что между ней и Землей находится яркое Солнце.
Рис. 4.1. Конфигурации Венеры и Марса. Противостояние Марса — планета находится ближе всего к Земле, ее видно всю ночь в противоположном от Солнца направлении. Венеру лучше всего видно вечером в восточную элонгацию слева от Солнца В1 и утром во время западной элонгации справа от Солнца В2
| Противостояние — планета видна с Земли целую ночь в противоположном от Солнца направлении Элонгация — видимое с поверхности Земли угловое расстояние между планетой и Солнцем |
Лучшие условия для наблюдения Венеры и Меркурия бывают в конфигурациях, называемых элонгациями. Восточная элонгация (ВЭ) — это положение, когда планета видна вечером В1 слева от Солнца. Западная элонгация (ЗЭ) Венеры наблюдается утром, когда планета видна справа от Солнца в восточной части небосклона B2.
Конфигурации ярких планет
Условные обозначения: ПС — противостояние, планета видна всю ночь; Сп — сообщение с Солнцем, планета не видна; (ВЭ) — восточная элонгация, планета видна вечером в западной части горизонта; ЗЭ — западная элонгация, планета видна утром в восточной части небосклона.
Сидерический и синодический периоды обращения планет
Сидерический период обращения определяет движение тел относительно звезд. Это время, за которое планета, двигаясь по орбите, совершает полный оборот вокруг Солнца (рис. 4.2).
Рис. 4.2. Путь, соответствующий сидерическому периоду обращения Марса вокруг Солнца, изображен пунктиром синего цвета, синодическому — пунктиром красного цвета
Синодический период обращения определяет движение тел относительно Земли и Солнца. Это промежуток времени, за который наблюдаются одни и те же последовательные конфигурации планет (противостояние, соединение, элонгация). На рис. 4.2 положения С—З1—М1 и С—32—М2 — два последовательных противостояния Марса. Между синодическим S и сидерическим Т периодами обращения планеты существует следующее соотношение:

где Т = 1 год — 365,25 суток — период обращения Земли вокруг Солнца. В формуле (4.1) знак «+» применяется для Венеры и Меркурия, которые обращаются вокруг Солнца быстрее, чем Земля. Для других планет применяется знак «-».
Законы Кеплера
Иоганн Кеплер (рис. 4.3) определил, что Марс движется вокруг Солнца по эллипсу, а потом было доказано, что и другие планеты имеют эллиптические орбиты.
Рис. 4.3. И. Кеплер (1571—1630)
Первый закон Кеплера. Все планеты обращаются вокруг Солнца по эллипсам, а Солнце находится в одном из фокусов этих эллипсов(рис. 4.4, 4.5).
Рис. 4.4. Планеты обращаются вокруг Солнца по эллипсам. AF1=Fmin — в перигелии; BF1=Fmax — в афелии
Главное следствие из первого закона Кеплера: расстояние между планетой и Солнцем не остается постоянным и изменяется в пределах: rmax ≤ r ≥ rmin
Точка А орбиты, где планета приближается на наименьшее расстояние к Солнцу, называется перигелием (греч. peri — вблизи helios — Солнце), а самую отдаленную от центра Солнца точку В орбиты планеты назвали афелием (от греч. аро — вдали). Сумма расстояний в перигелии и афелии равна большой оси АВ эллипса: rmax + rmin = 2a. Большая полуось земной орбиты (ОА или ОВ) называется астрономической единицей. 1 а. е. = 149,6×10 6 км.
| Земля в перигелии 3—4 января приближается к Солнцу на наименьшее расстояние 147 млн км Земля в афелии 3—4 июля удаляется от Солнца на самое большое расстояние 153 млн км |
Рис. 4.5. Как правильно нарисовать эллипс
Степень вытянутости эллипса характеризуется эксцентриситетом е — отношением расстояния между фокусами 2с к длине большой оси 2а, то есть e=c/a, 0 39 раз слабее, но только гравитация управляет движением планет, а также влияет на эволюцию Вселенной. Это можно объяснить тем, что электрические заряды имеют разный знак («+» и «-»), поэтому тела большой массы являются в основном нейтральными, и на большом расстоянии электромагнитное взаимодействие между ними довольно слабое.
Определение расстояний до планет
Для измерения расстояний до планет можно использовать третий закон Кеплера, но для этого надо определить расстояние от Земли до любой планеты. Предположим, что нужно измерить расстояние L от центра Земли О до светила S. За основу принимают радиус Земли R, и измеряют угол ∠ASO=p, так называемый горизонтальный параллакс светила, ибо одна сторона прямоугольного треугольника — катет AS, является горизонтом для точки А (рис. 4.11).
Рис. 4.11. Горизонтальный параллакс р светила определяет угол, под которым с этого светила был бы виден перпендикулярный к лучу зрения радиус Земли
Горизонтальный параллакс (от греч.— смещение) светила — это угол, под которым было бы видно перпендикулярный к лучу зрения радиус Земли, если бы сам наблюдатель находился на этом светиле. Из прямоугольного треугольника OAS определяем гипотенузу OS:

Правда, при определении параллакса возникает проблема: как астрономы могут измерить угол с поверхности Земли, не летая в космос? Чтобы определить горизонтальный параллакс светила S, нужно двум наблюдателям одновременно из точек А и В измерить небесные координаты (прямое восхождение и склонение) этого светила (см. § 2). Эти координаты, измеряемые одновременно из точек А и Б, будут немного отличаться. На основе этой разницы координат определяют величину горизонтального параллакса.
Чем дальше от Земли наблюдается светило, тем меньше значение параллакса. Например, самый большой горизонтальный параллакс имеет Луна, когда находится ближе всего к Земле: p = 1°01′. Горизонтальный параллакс планет гораздо меньше, и он не остается постоянным, поскольку расстояния между Землей и планетами меняются. Среди планет самый большой параллакс имеет Венера — 31″, а самый маленький 0,21″ — Нептун. Для сравнения: букву «О» в этой книге видно под углом 1″ с расстояния 100 м — такие крошечные углы астрономы вынуждены измерять для определения горизонтальных параллаксов тел в Солнечной системе. О том, как измерить расстояние до звезд, смотри в § 13.
Выводы
Все космические тела от планет до галактик движутся по закону всемирного тяготения, который был открыт Ньютоном. Законы Кеплера определяют форму орбиты, скорость движения планет Солнечной системы и их периоды обращения вокруг Солнца.
Тесты
- Как называется расположение планет в космическом пространстве относительно Земли и Солнца?
- А. Конфигурация.
Б. Противостояние. В. Космогония.
Г. Вознесение.
Д. Перемещение.
- А. Сатурн.
Б. Венера.
В. Меркурий.
Г. Юпитер.
- А. Сатурн.
Б. Венера.
В. Меркурий.
Г. Юпитер.
- А. Лев.
Б. Козерог.
В. Орион.
Г. Рыбы.
Д. Водолей.
- А. Перигелий.
Б. Перигей.
В. Апогей.
Г. Афелий.
Д. Апекс.
Диспуты на предложенные темы
- Как изменится климат Земли, если эксцентриситет земной орбиты будет равен 0,5, а большая полуось останется такой, как сейчас? Считать, что угол наклона оси обращения к плоскости эклиптики останется 66,5°.
Задания для наблюдений
- Определите при помощи астрономического календаря, какая планета Солнечной системы находится ближе всего к Земле в день вашего рождения в текущем году. В каком созвездии ее можно увидеть сегодня ночью?
Ключевые понятия и термины:
Афелий, элонгация, конфигурации планет, параллакс, перигелий, противостояние, сидерический и синодический период.
Источник





 .
.





