Законы Кеплера
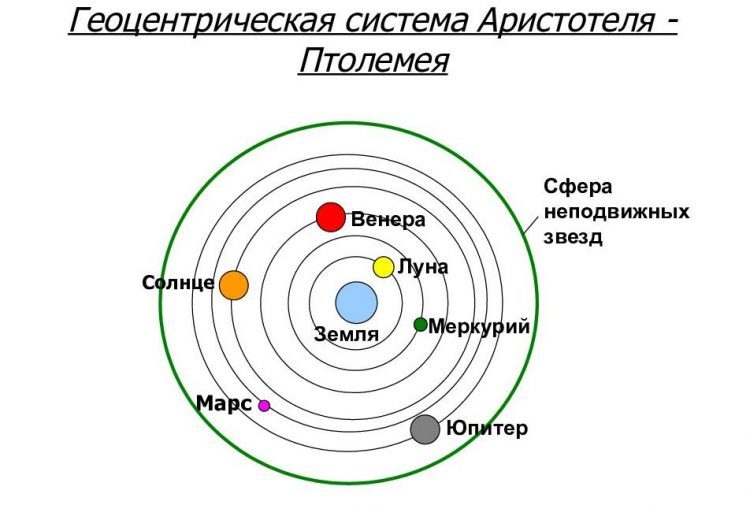
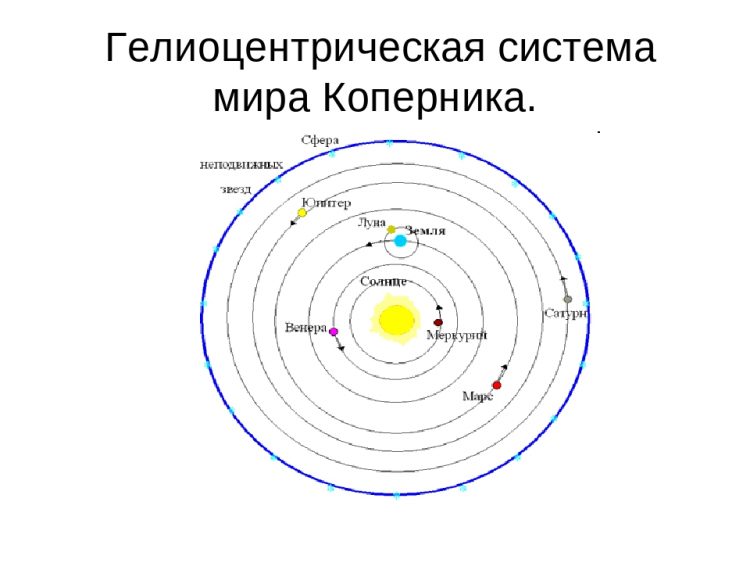
Астрономия конца XVI века отмечает столкновение двух моделей нашей Солнечной системы: геоцентрическая система Птолемея – где центром вращения всех объектов является Земля, и гелиоцентрическая система Коперника – где Солнце является центральным телом.
И хотя Коперник был ближе к истинной природе Солнечной системы, его работа имела недостатки. Основным из этих недостатков являлось утверждение, что планеты вращаются вокруг Солнца по круговым орбитам. С учетом этого, модель Коперника практически настолько же не согласовывалась с наблюдениями, как и система Птолемея. Польский астроном стремился исправить данное расхождение при помощи дополнительного движения планеты по кругу, центр которого уже двигался вокруг Солнца — эпицикл. Однако, расхождения в большей своей части не были устранены.
В начале XVII века немецкий астроном Иоганн Кеплер, изучая систему Николая Коперника, а также анализируя результаты астрономических наблюдений датчанина Тихо Браге, вывел основные законы относительно движения планет. Они были названы как Три закона Кеплера.
Будучи великолепным наблюдателем, Тихо Браге за много лет составил объёмный труд по наблюдению планет и сотен звёзд, причём точность его измерений была существенно выше, чем у всех предшественников.
Первый закон Кеплера (закон эллипсов)
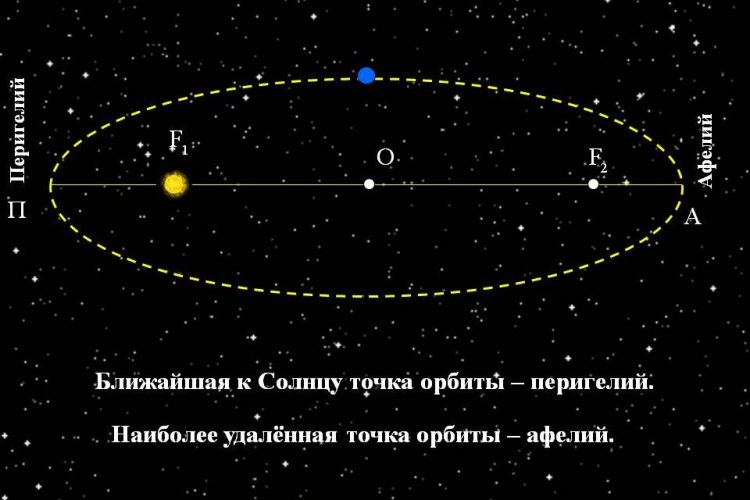
Планеты Солнечной системы движутся по эллиптическим орбитам. В одном из фокусов которой находится Солнце.
Согласно первому закону Кеплера, все планеты нашей системы движутся по замкнутой кривой, называемой эллипсом. Наше светило располагается в одном из фокусов эллипса. Всего их два: это две точки внутри кривой, сумма расстояний от которых до любой точки эллипса постоянна.
После длительных наблюдений ученый смог выявить, что орбиты всех планет нашей системы располагаются почти в одной плоскости. Некоторые небесные тела двигаются по орбитам-эллипсам, близким к окружности. И только Плутон с Марсом двигаются по более вытянутым орбитам. Исходя из этого, первый закон Кеплера получил название закона эллипсов.
Второй закон Кеплера (закон площадей)
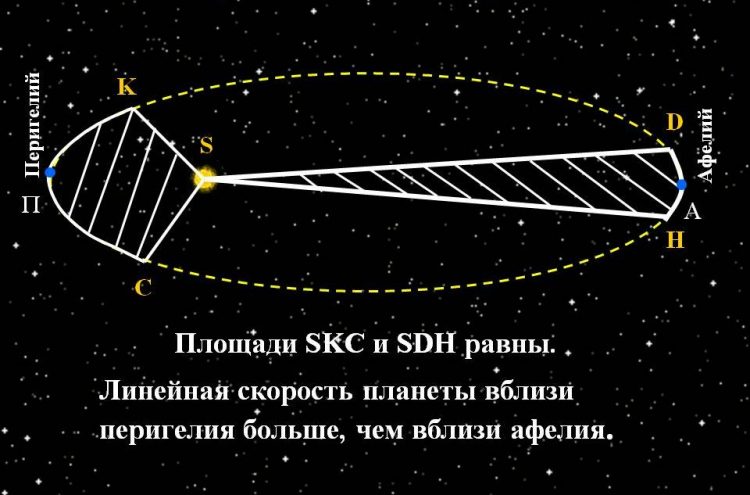
Радиус-вектор планеты описывает в равные промежутки времени равные площади.
Второй закон Кеплера говорит о следующем: каждая планета перемещается в плоскости, проходящей через центр нашего светила. В одно и то же время радиус-вектор, соединяющий Солнце и исследуемую планету, описывает равные площади. Таким образом, ясно, что тела движутся вокруг желтого карлика неравномерно, а имея в перигелии максимальную скорость, а в афелии – минимальную.
На практике это видно по движению Земли. Ежегодно в начале января наша планета, во время прохождения через перигелий, перемещается быстрее. Из-за этого движение Солнца по эклиптике происходит быстрее, чем в другое время года. В начале июля Земля движется через афелий, из-за чего Солнце по эклиптике перемещается медленнее.
Третий закон Кеплера (гармонический закон)
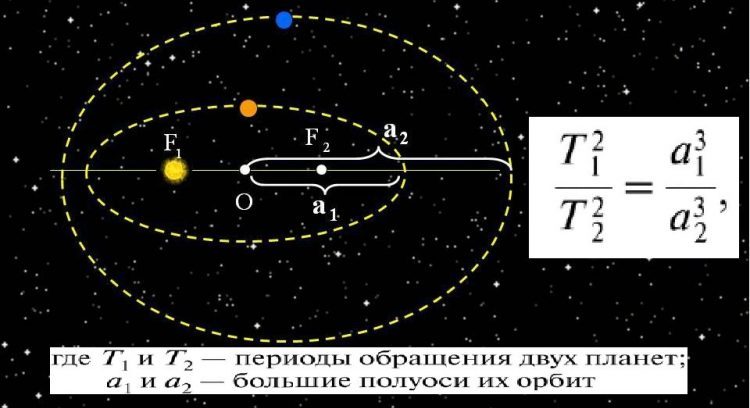
Квадраты периодов обращения планет относятся как кубы больших полуосей их орбит.
По третьему закону Кеплера, между периодом обращения планет вокруг светила и ее средним расстоянием от него устанавливается связь. Третий закон Кеплера выполняется как для планет, так и для спутников, с погрешностью не более 1 %.
На основании этого закона можно вычислить продолжительность года (время полного оборота вокруг Солнца) любой планеты, если известно её расстояние до Солнца. И наоборот — по этому же закону можно рассчитать орбиту, зная период обращения.
Дальнейшее развитие
И хотя законы Кеплера имели относительно невысокую погрешность, все же они были получены эмпирическим способом. Теоретическое же обоснование отсутствовало. Данная проблема позже была решена Исааком Ньютоном, который в 1682-м году открыл закон всемирного тяготения.
Законы Кеплера стали важнейшим этапом в понимании и описании движения планет.
Видео
Источник
Орбиты планет Солнечной системы
Орбиты планет, находящихся в Солнечной системе – это незримый путь, которые описывают данные тела вокруг центральной звезды – Солнца. Они могут быть различными по протяженности и вытянутости, что влияет на сезонность климата небесных тел и температуру их поверхности. Какую же форму имеют орбиты планет в Солнечной системе, и как это влияет на сами небесные тела?
Перигелий, афелий и эксцентриситет
Разберемся с основными характеристиками орбитального пути. Все планеты Солнечной системы движутся вокруг Солнца. Проходя по своей траектории данное тело имеет точки наибольшей удаленности и приближенности к центральной звезде. Они называются соответственно афелий и перигелий. От их значения напрямую зависят климатические условия на том или ином теле.
Перигелий и афелий планет нашей системы имеют следующие величины:
- Меркурий: 46 – 69,82 млн. км;
- Венера: 107,5 – 109 млн. км;
- Земля: 147,1 – 152,1 млн. км;
- Марс: 206,7 – 249,2 млн. км;
- Юпитер: 740,7 – 816 млн. км;
- Сатурн: 1,35 – 1,5 млрд. км;
- Уран: 2,73 – 3,01 млрд. км;
- Нептун: 4,45 – 4,5 млрд. км.
По представленным величинам видно, что у одних планет разница между расстоянием в минимальной и максимальной удаленности от Солнца крайне мала, а у других – значительна. С этим выводом неразрывно связан другой термин, необходимый для описания орбиты планет, — эксцентриситет.
Эксцентриситет траектории, по которой движется планета, определяет ее форму. Для вычисления этого параметра необходимо знать большую и малую полуоси орбиты планеты. Для каждой формы орбитального пути есть свое числовое значение эксцентриситета:
- 0 – круг;
- От 0 до 1 – эллипс;
- 1 – парабола;
- От 1 до ∞ — гипербола;
- ∞ — прямая.
Все орбиты планет Солнечный системы имеют значение эксцентриситета больше нуля, т.е. обладают эллипсовидной формой. При этом самые сжатые, схожие с круговыми, орбиты в Солнечной системе наблюдаются у Венеры и Нептуна, а наиболее вытянутые – у Меркурия и Марса.
Планетарный год
Полный оборот небесного тела по своей траектории называется сидерическим периодом вращения. Для планет этот термин имеет синоним «планетарный год». Его протяженность зависит от среднего радиуса орбиты и скорости, с которой планета совершает орбитальное вращение.
Для удобства описания планетарные года рассчитывают в земных сутках и годах. Так, например, на Меркурии год длится 0. 24 земных года, или 89 земных суток. Это наиболее короткий планетарный год в Солнечной системе. А самым долгим считается год на планете Нептун, длящийся 164 года земных.
Фактор, отвечающий за смену времен года
За сезонность на планетах Солнечной системы отвечает угол наклона оси вращения к орбите. Чем меньше угол, тем стабильнее погода на небесном теле и нет смены пор года. Также сезонности не бывает на небесных телах с углом наклона более 90°.
Смена сезонов характерна для объектов с углом наклона оси в пределах 20-30 градусов:
«Лето» и «зима» также есть на Меркурии, несмотря на практически отсутствующий наклон оси. Это связано с высоким эксцентриситетом его орбиты. Разница между температурами в точках перигелия и афелия на Меркурии составляет 620 градусов Цельсия.
Таким образом, величина и форма пути, который описывает объект вокруг Солнца, очень влияют на формирование температурных условий на нём. Именно невысокий эксцентриситет и небольшая удаленность движения Земли, а также оптимальный угол наклона оси сделали её температуру наиболее комфортной для существования живых организмов.
Источник
Наблюдение искусственных спутников Земли
Глава 1: Как движутся ИСЗ?Перед тем, как приступить к рассмотрению вопросов наблюдения ИСЗ, нужно выяснить как они движутся — по каким орбитам и каковы характеристики этих орбит. Без понимания этих вопросов наблюдение ИСЗ превращается в охоту за неведомым зверем, который неизвестно где обитает. § 1. Законы Кеплера и типы орбитИз курса средней школы нам известно, что тело, движущееся по орбите вокруг другого тела, подчинено трём законам Кеплера. Нас будут интересовать только два из них — первый и третий. Согласно первому закону Кеплера, тело, обращающееся вокруг Земли (в нашем случае) движется по эллипсу, в одном из фокусов которого находится центр Земли (см. рис. 2). Мы специально не упоминали тут, что тело может двигаться по трём видам орбит — эллипс, гипербола и парабола. Нас интересуют только периодические орбиты, а из перечисленных такой является эллипс.
Элементы эллипса показаны на рис. 2. «F1« и «F2« — фокусы эллипса; «a» — большая полуось; «b» — малая полуось; «е» — эксцентриситет эллипса, который определяется следующим образом:
Таким образом, первое важное положение — ИСЗ движутся вокруг Земли по эллипсам . Согласно третьему закону Кеплера, квадраты периодов обращения «T» спутников относятся как кубы их больших полуосей «a»:
§ 2. Орбитальные элементыДля того, чтобы задать параметры и ориентацию орбиты ИСЗ в пространстве, нужно указать 6 т.н. кеплеровских элементов (орбитальных элементов) (см. рис. 3):
Итак, наше второе важное положение — орбита ИСЗ полностью задаётся шестью орбитальными элементами . § 3. Круговая орбитаРассмотрим частный случай эллиптической орбиты — круговая орбита. Если значение эксцентриситета орбиты ИСЗ е = 0, то орбита представляет собой окружность с центром в центре Земли. Для того, чтобы тело стало спутником Земли, оно должно обладать определённой скоростью при полёте вокруг неё. Если бы у Земли не было атмосферы, то минимальная скорость, необходимая для того, чтобы тело двигалось по окружности вокруг Земли, равна vк0 = 7,91 км/с. Но в реальности такого быть не может — спутник будет сильно тормозится в атмосфере Земли. Если ИСЗ начнёт двигаться на высоте менее примерно 160 км от поверхности Земли, то он сможет сделать лишь пару оборотов, после чего начнёт необратимо терять скорость и сгорит в плотных слоях атмосферы. Для примерного расчёта скорости ИСЗ на круговой орбите можно воспользоваться формулой [1]:
где R = 6371 км — средний радиус Земли, r = R + h — расстояние от центра Земли до ИСЗ, h — высота ИСЗ над поверхностью Земли. При наблюдениях важно знать период обращения ИСЗ Т — время, необходимое на один полный оборот вокруг Земли. Для круговой орбиты период Т можно вычислить по формуле [1]:
Из (4) видно, что минимальное время, необходимое ИСЗ для одного оборота, равно Tк0 = 84,4 минуты — при нулевой высоте над поверхностью. Никакое тело не может быстрее обогнуть поверхность Земли. При примерных оценках периода обращения ИСЗ по круговой орбите полезно помнить, что период обращения увеличивается примерно на 1 минуту при увеличении высоты ИСЗ на каждый 50 км. Этой оценкой можно пользоваться для ИСЗ не выше 1000 км. Наше третье важное положение — ИСЗ не может двигаться долгое время по орбите вокруг Земли ниже 140-160 км. При этом, период обращения по круговой орбите является минимальным и для диапазона высот 160-1000 км изменяется всего с 87,6 до 105 минут . § 4. Эллиптическая орбитаТеперь рассмотрим общий вид орбиты ИСЗ — эллиптическая орбита (см. рис. 4). Как было указано выше, из первого закона Кеплера следует, что в фокусе эллиптической орбиты будет находится Земля (З), вокруг которой вращается ИСЗ. Двигаясь по эллиптической орбите, ИСЗ ближе всего подлетает к центру Земли в точке «П» — в перигее, а дальше всего находится в точке «А» — в апогее. Линия, соединяющая перигей и апогей называется линией апсид. Из наблюдений ИСЗ можно определить большую полуось и эксцентриситет орбиты, из которых можно вычислить значения перигейного «q» и апогейного «Q» расстояний:
Из (5) видно, что Q + q = 2a. При движении по орбите изменяется расстояние «r» от Земли до ИСЗ — величина радиус-вектора «r» задаётся выражением [3]:
Скорость ИСЗ в любой точке эллиптической орбиты задаётся выражением [2]:
Период обращения для спутника на эллиптической орбите вычисляется по формуле (4), в которой вместо «r» нужно подставить значение большой полуоси «a». Наше четвёртое важное положение — скорость движения ИСЗ по эллиптической орбите не равномерна: максимальна она в перигее, а минимальна в апогее. Период обращения теперь определяется не только большой полуосью «a», но и значением эксцентриситета «e» . § 5. Эволюция орбиты ИСЗВ этом параграфе мы рассмотрим, как изменяются параметры реальной орбиты ИСЗ под воздействием определённых факторов. Прежде всего следует отметить следующее: если бы Земля имела форму идеального шара с равномерным распределением вещества, была лишена атмосферы, а Луна и Солнце отсутствовали бы, то ИСЗ вечно бы вращался по своей орбите, ориентация которой в пространстве не изменялась. Если бы спутник совершал 14 оборотов в сутки (при этом его период равен примерно 103 минуты), то за время одного витка ИСЗ Земля повернётся на 1/14 полного оборота (это примерно 26°). Это означает, что с каждым новым траектория ИСЗ смещалась к западу на 26° за каждый виток. Прецессия орбитыВ реальности форма Земли — геоид, полярный радиус которого RП = 6356,8 км, а экваториальный — RЭ = 6378,2 км, т.е. экваториальный радиус больше полярного на 21,4 км. Земля имеет экваториальный «горб», который своей массой оказывает влияние на движение ИСЗ. Влияние это не такое уж явное — масса «горба» не вызывает изменения наклонения «i» орбиты за счёт притягивания плоскости орбиты к плоскости экватора, как можно было бы ожидать — плоскость орбиты медленно поворачивается вокруг земной оси в направлении, противоположном вращению ИСЗ (см. рис. 5).
Этот процесс называется прецессией. Угол прецессии плоскости орбиты ИСЗ остаётся неизменным. Угловая скорость прецессии «X1« (градусов в сутки) определяется, в основном, наклонением орбиты [1]:
где «i» — наклонение орбиты, «e» — эксцентриситет, RЭ — экваториальный радиус Земли, «а» — большая полуось орбиты ИСЗ. Если спутник движется в запада на восток, орбита поворачивается с востока на запад. Чем меньше наклонение ИСЗ, тем больше значение прецессии (см. рис. 6). Если спутник вращается с востока на запад (обратное движение ИСЗ), то прецессия орбиты происходит в обратную сторону. При этом линия узлов также поворачивается (см. рис. 7).
Теперь посмотрим, к каким изменениям условий наблюдения спутника приводит прецессия. Как известно, Земля делает полный оборот за 23 ч 56 м 4,09 с (звёздные сутки) — за 24 ч (средне-солнечные сутки) небо нам кажется повернувшимся на 361° (т.к. звёздные сутки короче средне-солнечных на 4 минуты — за это время небо повернётся на 1°). Если бы плоскость орбиты ИСЗ не прецессировала, то через 24 ч он появлялся бы на небе на 1° западнее, чем накануне (если движение ИСЗ прямое). Но за счёт прецессии орбита поворачивается на Х1 градусов за сутки, поэтому ИСЗ через 24 ч окажется на Х1 + 1 градус западнее (при обратном движении — на 1 — Х1 градус к западу). Период обращения спутника не кратен целой части суток. Если через сутки спутник будет пересекать ту же широту Земли на n минут позже, он окажется ещё на n/4 градусов западнее, т.к. за 1 минуту Земля поворачивается на 1/4 минуты. Следовательно, суммарный суточный сдвиг к западу составит (Х1 + 1 + n/4) градусов [1]. Вращение эллиптической орбитыСледующим важным эффектом, влияющим на эволюцию орбиты ИСЗ, является поворот плоскости эллиптической орбиты. Эффект этот, как и предыдущий, обязан своим существованием экваториальному «горбу» Земли, но в отличие от прецессии, действует только на эллиптичные орбиты. Эффект заключается в том, что эллиптическая орбита постоянно поворачивается в своей плоскости вперёд для спутников с нулевым наклонением, и назад — для спутников с наклонением, близким к 90°. За счёт этого точки перигея движутся вперёд или назад по орбите (см. рис. 8).
Скорость вращения «X2« эллиптической орбиты определяется выражением [1]:
На рис. 9 показаны графики зависимости X2(i) для ИСЗ с разными значениями больших полуосей «a».
Вращение происходит в том же направлении, что и движение спутника, если наклонение i 63,4°. При i = 63,4° поворот орбиты отсутствует. Наше пятое важное положение — движение ИСЗ подвержено возмущениям из-за несферичности Земли. За счёт прецессии орбита спутника может смещаться с угловой скоростью до 9°/сутки, а за счёт поворота эллиптической орбиты — до 15°/сутки. При этом, чем меньше наклонение, тем сильнее оба эффекта, но действовать они могут как в одну сторону, так и в противоположные . Атмосферное торможениеПрецессия орбиты и поворот её плоскости связаны с действием несферичности Земли. Но кроме этого Земля окружена атмосферой, которая прослеживается до 2000 км над её поверхностью. Из этого следует, что на движение ИСЗ, особенно на низких орбитах, влиянием атмосферы мы пренебрегать не можем. Атмосферное давление падает с высотой экспоненциально — на высоте 200 км оно составляет 10 -12 мбар (на уровне моря атмосферное давление составляет 1013 мбар), а на высоте 900 км — уже только 10 -42 мбар [6]. Тем не менее, даже такая разреженная атмосфера может приводить к изменению орбиты ИСЗ. Сила сопротивления движущемуся в атмосфере телу определяется выражением [4]:
где «cx« — безразмерный коэффициент сопротивления, для верхней атмосферы равный 2-2,5; «S» — площадь максимального сечения спутника, перпендикулярного налетающему воздушному потоку; «v» — скорость ИСЗ, «ρ» — плотность атмосферы на высоте полёта ИСЗ. Торможение ИСЗ определяется его парусностью — чем больше площадь и меньше масса, тем больше торможение. Для спутника, движущемся по круговой орбите, сопротивление атмосферы будет сказываться следующим образом: спутник будет медленно опускаться по спирали с постоянно увеличивающейся скоростью. Угол снижения спутника на круговой орбите можно оценить из выражения [1]:
где «m» — масса ИСЗ, «g» — ускорение свободного падения. Снижение по спирали будет продолжаться до тех пор, пока спутник не опустится до высоты 160 км — ниже этой высоты сила сопротивления настолько велика, что спутник начинает резкое снижение и сгорит в атмосфере. На высоте 160 км период обращения равен примерно 88 минут — любой ИСЗ с меньшим периодом обречён. Если орбита эллиптическая, то результат действия сопротивления атмосферы будет следующим: т.к. сопротивление сильно уменьшается с высотой, то максимальное сопротивление ИСЗ будет испытывать в перигее, а минимальное — в апогее. Это слабо меняет высоту перигея, но уменьшает высоту апогея — в результате эллиптичность орбиты уменьшается и спутник начинает спуск по спирали. На рис. 10 показано снижение ИСЗ в случае эллиптической орбиты.
Оценить время жизни спутника можно из выражения (12) [1]:
где e0 — начальный эксцентриситет орбиты, T0 — начальный период обращения, ΔT — суточное изменение периода. Тогда измение периода будет определятся выражением [1]:
а изменение эксцентриситета [1]:
Формулы (13) и (14) справедливы для значений e = 0,02-0,2. На атмосферное торможение сильно влияет время суток (в подсолнечной точке атмосфера подымается выше), а также активность Солнца. Как видно, время жизни спутника определяется его эксцентриситетом и большой полуосью. В таблице ниже представлены времена жизни ИСЗ для разных значений перигея и апогея [5]:
Наше шестое важное положение — сопротивление атмосферы Земли вызывает уменьшение большой полуоси орбиты ИСЗ, в результате чего он по спирали спускается вниз. При достижении высоты около 160 км спутник сможет сделать всего пару оборотов и сгорит в атмосфере, войдя в резкий и необратимый спуск . Давление светаВпервые идею о том, что свет производит давление на тела, высказал в 1619 г. И. Кеплер — для объяснения эффекта отклонения кометных хвостов от Солнца. Современная теория даёт значение давления следующим выражением (формула Максвелла-Бартоли) [3]: где «E» — мощность электромагнитного излучения, приходящаяся на единицу площади тела, «η» — коэффициент отражения тела, «c» — скорость света. Для абсолютно поглощающего тела вблизи Земли давление света равно 4,3 · 10 -6 Н/м 2 . Для абсолютно отражающего тела эта величина в два раза больше. Световое давление становится ощутимым для лёгких спутников выше 500 км, т.к. ниже большее значение имеют колебания плотности атмосферы. В заключении параграфа нужно отметить, что перечисленные факторы влияния на эволюцию орбиты спутника не составляют полный список. Например, на ИСЗ воздействуют своим притяжением Солнце и Луна, но это воздействие в 10000 раз слабее действия экваториального «горба» Земли, но его нужно учитывать для орбит с большим эксцентриситетом. Экваториальный «горб» также вызывает незначительные колебания плоскости орбиты ИСЗ при пересечении экваториальной плоскости. Наконец, неравномерность распределения масс под поверхностью Земли также сказывается на движении спутника. Как видим, движение спутника не так просто, как может показаться на первый взгляд. В наше время расчёты эволюции орбиты значительно упростились с точки зрения затраты времени, т.к. современные компьютеры имеют огромную вычислительную мощность. Даже любители, используя специальные программы (см. далее), могут довольно точно расчитывать положение спутников на нужную им дату и время, причём на любой промежуток времени — в начале космической эры любители могли об этом только мечтать. Источник ➤ Adblockdetector | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 ,     (1)
,     (1)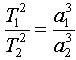 ,     (2)
,     (2) 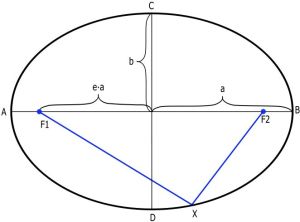

 ,     (3)
,     (3) ,     (4)
,     (4) .     (5)
.     (5) 
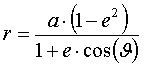 .     (6)
.     (6)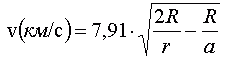 .     (7)
.     (7)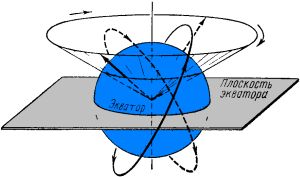
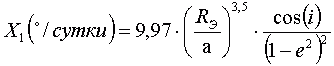 ,     (8)
,     (8)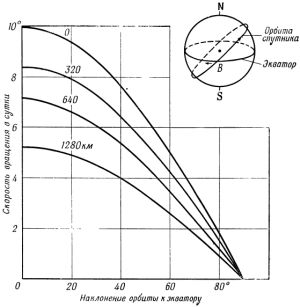


 .     (9)
.     (9)
 ,     (10)
,     (10)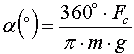 ,     (11)
,     (11)
 ,     (12)
,     (12) ,     (13)
,     (13) .     (14)
.     (14)