Урок 19
§12. Множества и логика
Содержание урока
Сложные запросы в поисковых системах
Сложные запросы в поисковых системах
Для решения задач, в которых используются множества, например множества страниц, полученных от поисковой системы в ответ на какой-то запрос, удобно применять диаграммы Эйлера-Венна.
Задача 1. Известно количество страниц, которые находит поисковый сервер по следующим запросам (здесь символ «&» обозначает операцию И, а «|» — операцию ИЛИ):
собаки | кошки 770
собаки & кошки 100
Сколько страниц будет найдено по запросу собаки?
Введём два множества: А — множество страниц, где есть слово «собаки», В — множество страниц со словом «кошки». По формуле, которая получена в предыдущем пункте, получаем:
Известно количество страниц, которые находит поисковый сервер по следующим запросам:
лилия & незабудка 100
лилия | незабудка 450
Сколько страниц найдёт этот сервер по запросу лилия?
Известно количество страниц, которые находит поисковый сервер по следующим запросам:
кашалот | енот 450
Сколько страниц найдет этот сервер по запросу
Известно количество страниц, которые находит поисковый сервер по следующим запросам:
Франция & Италия 80
Сколько страниц найдёт этот сервер по запросу
Рассмотрим теперь более сложную задачу с тремя областями.
Задача 2. Известно количество страниц, которые находит поисковый сервер по следующим запросам:
собаки & лемуры 320
кошки & лемуры 280
(кошки | собаки) & лемуры 430
Сколько страниц будет найдено по запросу
кошки & собаки & лемуры?
Заметим, что во всех запросах есть часть & лемуры. Это означает, что область поиска во всех случаях ограничена страницами, на которых встречается слово «лемуры».
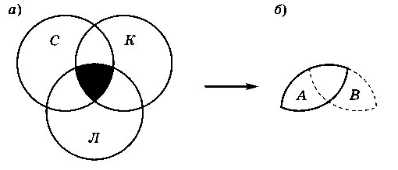
Обозначим буквами С, К и Л области (группы страниц), содержащие ключевые слова «собаки», «кошки» и «лемуры» соответственно. Нас интересует только область, выделенная фоном на рис. 2.41, а.
Эта область образована в результате пересечения двух областей (рис. 2.41, б):
А = собаки & лемуры
В = кошки & лемуры
Поэтому задачу можно свести к задаче с двумя областями.
Известно количество страниц, которые находит поисковый сервер по следующим запросам:
Сколько страниц будет выдано по запросу А & В?
Используя формулу включений и исключений, полученную в предыдущем пункте, находим:
Известно количество страниц, которые находит поисковый сервер по следующим запросам:
берёза & сирень 220
берёза & сирень & арбуз 30
сирень & (берёза | арбуз) 340
Сколько страниц найдёт этот сервер по запросу
Известно количество страниц, которые находит поисковый сервер по следующим запросам:
яхта & диван 270
диван & пирог 350
яхта & диван & пирог 80
Сколько страниц найдёт этот сервер по запросу
(пирог | яхта) & диван?
Задачу с тремя областями не всегда удаётся свести к более простой задаче с двумя областями. Серьёзным упрощением может стать то, что какие-то два множества не имеют общих элементов.
Если два множества не имеют общих элементов, что можно сказать об их изображении на диаграмме Эйлера-Венна?
Задача 3. Известно количество страниц, которые находит поисковый сервер по следующим запросам:
кошки | собаки 450
кошки & лемуры 40
собаки & лемуры 50
Сколько страниц найдёт этот сервер по запросу
(кошки | собаки) & лемуры?
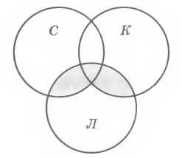
Здесь часть & лемуры встречается не во всех запросах, поэтому свести задачу к задаче с двумя областями не удаётся. Используя те же обозначения, что и в задаче 2, построим диаграмму с тремя переменными и выделим интересующую область, которая соответствует запросу (кошки I собаки) & лемуры.
На рисунке 2.42 эта область выделена фоном.
В общем виде задача с тремя областями очень сложна. Попробуем найти какое-нибудь упрощающее условие. Например, выделим три условия:
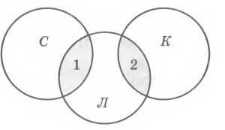
кошки | собаки 450
Это означает, что область кошки | собаки равна сумме областей кошки и собаки, т. е. эти области не пересекаются! Таким образом, в нашем случае диаграмма выглядит так (рис. 2.43).
Размеры областей 1 (собаки & лемуры) и 2 (кошки & лемуры) нам известны, они составляют соответственно 40 и 50 страниц, поэтому по запросу
(кошки | собаки) & лемуры
поисковый сервер найдёт 40 + 50 = 90 страниц.
Известно количество страниц, которые находит поисковый сервер по следующим запросам:
крабы | солнце 450
солнце & лето 20
Сколько страниц найдёт этот сервер по запросу
крабы | солнце | лето?
Следующая страница 
Cкачать материалы урока
Источник
Известно количество страниц которые находит поисковый сервер по следующим запросам солнце 230
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
| Запрос | Количество (тыс.) |
|---|---|
| Аврора | 50 |
| Крейсер | 45 |
| Заря | 23 |
| Аврора & Заря | 9 |
| Заря & Крейсер | 0 |
| Заря | Крейсер | Аврора | 93 |
Сколько страниц (в тысячах) будет найдено по запросу Аврора & Крейсер?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Построим диаграмму Венна для данной задачи. Количество запросов в данной области будем обозначать Ni. Пусть Крейсер — круг 1, Аврора — круг 2, Заря — круг 3. Наша цель — найти сумму N4.
Источник
Известно количество страниц которые находит поисковый сервер по следующим запросам солнце 230
Сколько сайтов будет найдено по запросу «(принтер | сканер) & монитор», если по запросу «принтер | сканер» было найдено 450 сайтов, по запросу «принтер & монитор» — 40, а по запросу «сканер & монитор» — 50.
принтер | сканер 450
поскольку последнее число равно сумме двух предыдущих, можно сразу же прийти к выводу, что в этом сегменте сети нет сайтов, для которых ключевыми словами являются одновременно принтер и сканер:
принтер & сканер 0
Следовательно, для того, чтобы определить, сколько сайтов удовлетворяют заданному условию
достаточно просто сложить числа, соответствующие запросам «принтер & монитор» и
В таблице приведены запросы и количество страниц, которые нашел поисковый сервер по этим запросам в некотором сегменте Интернета:
торты | пироги
торты & пироги
Сколько страниц (в тысячах) будет найдено по запросу торты
По формуле включений и исключений имеем:
m(торты | пироги) = m(торты) + m(пироги) — m(торты & пироги) = m(торты) + 7700 — 6500 = 12000. => m(торты) = 10800.
Некоторый сегмент сети Интернет состоит из 5000 сайтов. Поисковый сервер в автоматическом режиме составил таблицу ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
принтеры
мониторы
Сколько сайтов будет найдено по запросу (принтеры | мониторы) & сканеры
если по запросу принтеры | сканеры было найдено 600 сайтов,
по запросу принтеры | мониторы – 900,
а по запросу сканеры | мониторы – 750.
Для сокращения записи обозначим через C, П, М высказывания «ключевое слово на сайте – сканер» (соответственно принтер, монитор) и нарисуем эти области виде диаграммы (кругов Эйлера). Заметим, что поскольку по запросу принтеры | мониторы было найдено 900 страниц, по запросам принтеры — 400, мониторы — 500, а 900 = 500 + 400, области П и М не пересекаются. Интересующему нас запросу (П | M) & C соответствует объединение областей 4 и 2 («зеленая зона» на рисунке). Количество сайтов, удовлетворяющих запросу в области i, будем обозначать через Ni.
Тогда из первого и пятого уравнений получаем, что N1 + N2 = 250, а из четвёртого:
N4 = 300 − 250 = 50.
Из второго и четвёртого уравнений получаем, что N3 = 300, а из третьего:
N2 = 400 − 300 = 100.
Следовательно ответ N2 + N4 = 150.
Источник
Известно количество страниц которые находит поисковый сервер по следующим запросам солнце 230
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Канада & США | 277 |
| США & (Канада | Мексика) | 417 |
| Канада & США & Мексика | 106 |
Какое количество страниц (в тысячах) будет найдено по запросу США & Мексика?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Нарисуем диаграмму Венна для этой задачи.
Тогда по условию дано:
2) S4 + S5 + S7 = 417
Нужно найти S4 + S7.
Вычтем третье равенство из первого.
Получим 4) S5 = 171.
Теперь из второго вычтем четвёртое.
Получим S4 + S7 = 246.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Сосна & Ель
Сосна & (Ель | Кедр)
Сосна & Кедр
Какое количество страниц (в тысячах) будет найдено по запросу: Сосна & Ель & Кедр?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Нарисуем диаграмму Венна для этой задачи.
Тогда по условию дано:
2) S4 + S6 + S7 = 530
Вычтем третье равенство из второго.
Получим 4) S6 = 170.
Теперь из первого вычтем четвёртое.
Получим S7 = 100.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Сосна & Ель & Кедр
Сосна & Ель
Сосна & Кедр
Какое количество страниц (в тысячах) будет найдено по запросу Сосна & (Ель | Кедр)?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Нарисуем диаграмму Венна для этой задачи.
Тогда по условию дано:
Нужно найти S4 + S6 + S7.
Вычтем первое равенство из второго.
Получим 4) S6 = 170.
Теперь из сложим третье и четвёртое.
Получим S4 + S6 + S7 = 510.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в сотнях тысяч) |
|---|---|
| Поле | 100 |
| Рожь | 70 |
| Напряжённость | 48 |
| Рожь | Поле | Напряжённость | 124 |
| Рожь & Поле | 50 |
| Рожь & Напряжённость | 0 |
Какое количество страниц (в сотнях тысяч) будет найдено по запросу Поле & Напряжённость?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Представим таблицу в виде кругов Эйлера.
Пусть поле — круг 1, рожь — круг 2, напряженность — круг 3. Тогда задача — найти зону (обозначим зону за N) N5 + N6. По таблице известно:
Тогда найдем N5 = 0, а N6 = 44.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в сотнях тысяч) |
|---|---|
| Поле | 90 |
| Рожь | 71 |
| Напряжённость | 62 |
| Рожь | Поле | Напряжённость | 140 |
| Рожь & Поле | 53 |
| Рожь & Напряжённость | 0 |
Какое количество страниц (в сотнях тысяч) будет найдено по запросу Поле & Напряжённость?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Представим таблицу в виде кругов Эйлера. Пусть поле — круг 1, рожь — круг 2, напряженность — круг 3. Тогда задача — найти зону (обозначим зону за N) N5 + N6. По таблице известно:
Тогда найдем N5 = 0, а N6 = 30.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Линкор | Корвет
Линкор & Корвет
Какое количество страниц (в тысячах) будет найдено по запросу Корвет?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
По формуле включений и исключений имеем:
m(Линкор | Корвет) = m(Линкор) + m(Корвет) − m(Линкор & Корвет),
m(Корвет) = m(Линкор | Корвет) − m(Линкор) + m(Линкор & Корвет) = 3400 — 2100 + 1300 = 2600.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Линкор | Корвет
Линкор & Корвет
Какое количество страниц (в тысячах) будет найдено по запросу Корвет?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
По формуле включений и исключений имеем:
m(Линкор | Корвет) = m(Линкор) + m(Корвет) − m(Линкор & Корвет),
m(Корвет) = m(Линкор | Корвет) − m(Линкор) + m(Линкор & Корвет) = 3320 — 2100 + 1300 = 2520.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» – символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Масло | 146 |
| Холст | 120 |
| Сыр & Масло | 40 |
| Сыр | Холст | 186 |
| Холст | Сыр | Масло | 222 |
Какое количество страниц (в тысячах) будет найдено по запросу Холст & Масло?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Представим таблицу в виде кругов Эйлера. Пусть масло — круг 1, сыр — круг 2, холст — круг 3. Тогда задача — найти зону (обозначим зону за N) N5 + N6. По таблице известно:
Выразим сумму N2 + N7, подставив четвёртое уравнение во второе:
Подставляем пятое уравнение в шестое и получаем N1 = 222 − 186 = 36. После этого подставляем четвёртое уравнение в первое и находим N6 = 146 − 40 − 36 = 70. Теперь подставляем четвёртое и седьмое уравнения в пятое и находим N3 = 186 − 26 − 40 − 70 = 50. Далее подставляем N3 и N6 в третье уравнение и получаем N5 + N7 = 120 − 50 − 70 = 0. Следовательно, N5 = 0.
Таким образом, N5 + N6 = 0 + 70 = 70.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Бейсик | Паскаль | Ньютон | 953 |
| Бейсик & Паскаль & Ньютон | 1 |
| Бейсик | 355 |
| Паскаль | 618 |
| Ньютон | 319 |
| Бейсик | Ньютон | 673 |
| Бейсик & Паскаль | 223 |
Какое количество страниц (в тысячах) будет найдено по запросу
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Пусть Б, П, Н — обозначения соответствующих множеств. По формуле включений-исключений:
Откуда
Найдём по формуле включений-исключений при помощи формулы включений-исключений:
Найдём
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для обозначения логической операции «И» — символ «&».
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Бейсик | Паскаль | Ньютон | 914 |
| Бейсик & Паскаль & Ньютон | 1 |
| Бейсик | 343 |
| Паскаль | 585 |
| Ньютон | 311 |
| Бейсик | Ньютон | 653 |
| Ньютон & Паскаль | 110 |
Какое количество страниц (в тысячах) будет найдено по запросу
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Пусть Б, П, Н — обозначения соответствующих множеств. По формуле включений-исключений:
Откуда
Найдём по формуле включений-исключений при помощи формулы включений-исключений:
Найдём
Аналоги к заданию № 18498: 18629 Все
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
Сербия & Хорватия
Сербия|Хорватия
Какое количество страниц (в тысячах) будет найдено по запросу Хорватия? Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
По формуле включений и исключений имеем:
m(Сербия|Хорватия) = m(Сербия) + m(Хорватия) − m(Сербия&Хорватия).
Тогда 3000 = 2000 + m(Хорватия) − 500, откуда m(Хорватия) = 1500.
Ниже приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
1) спорт & футбол & чемпионат
2) спорт | футбол & чемпионат
3) cпорт | футбол | чемпионат & 2006
4) спорт | футбол | чемпионат
Логическая операция «И» истинна только тогда, когда истинны оба аргумента. Например, чтобы было истинно «канарейки & содержание» необходимо, чтобы в тексте содержалось и слово «канарейки» и слово «содержание».
Для истинности логической операции «ИЛИ» достаточно истинности лишь одного из ее аргументов. Например, чтобы было истинно «канарейки ∨ содержание» необходимо, чтобы в тексте содержалось или слово «канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц найдет поисковик, чем больше «|», тем большее.
Следовательно, на этом примере можно понять, как располагать по убыванию количества страниц варианты в данной задаче.
Правильный ответ: 4321.
Ниже приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу. Для обозначения логической операции «ИЛИ» в запросе используется символ |, а для логической операции «И» – &.
1) яблоки | сливы
2) сливы | (яблоки & груши)
3) яблоки | груши | сливы
4) (яблоки | груши) & сливы
Логическая операция “И” истинна только тогда, когда истинны оба аргумента. Например, чтобы было истинно «канарейки & содержание» необходимо, чтобы в тексте содержалось и слово «канарейки» и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно истинности лишь одного из ее аргументов. Например, чтобы было истинно «канарейки ∨ содержание» необходимо, чтобы в тексте содержалось или слово «канарейки» или слово «содержание».
Вывод: чем больше «&», тем меньшее количество страниц найдет поисковик, чем больше «|», тем большее.
Если сравнивать варианты 2 и 4, то большее количество страниц обеспечит запрос 2, так как “ИЛИ” истинно в трех случаях из четырех, в отличие от “И”, которое только в одном (вспомните таблицы истинности).
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| протон & фотон & бозон | 80 |
| протон & бозон | 240 |
| (протон | фотон) & бозон | 440 |
Компьютер печатает количество страниц (в тысячах), которое будет найдено по следующему запросу:
Укажите целое число, которое напечатает компьютер. Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Обозначим количество запросов в данной области как Ni. Наша цель — N4 + N5. Тогда из таблицы находим, что:
Из первого и второго равенств находим: N6 = 160, из последнего равенства: N4 + N5 = 280.
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&». В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет:
| Запрос | Найдено страниц (в тысячах) |
|---|---|
| Диана & (Аврора | Паллада) | 800 |
| Диана & Аврора & Паллада | 220 |
| Диана & Аврора | 550 |
Компьютер печатает количество страниц (в тысячах), которое будет найдено по следующему запросу:
Укажите целое число, которое напечатает компьютер. Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Обозначим количество запросов в данной области как Ni. Наша цель — N4 + N5. Тогда из таблицы находим, что:
Из первого и второго равенств находим: N2 = 330, из последнего равенства: N4 + N5 = 470.
В языке запросов поисковой системы кавычки вокруг части запроса означают, что эта часть должна встречаться точно в указанной форме (т. е. это цитата). Ниже приведены поисковые запросы, одновременно выданные к одной поисковой системе. Расположите их в порядке возрастания количества найденных документов:
1) Откуда берется мокрый снег
2) «Откуда берется мокрый снег»
3) Мокрый&снег&(откуда берется)
Логическая операция “И” истинна только тогда, когда истинны оба аргумента. Например, чтобы было истинно «канарейки & содержание» необходимо, чтобы в тексте содержалось и слово «канарейки» и слово «содержание».
Для истинности логической операции “ИЛИ” достаточно истинности лишь одного из ее аргументов. Например, чтобы было истинно «канарейки ∨ содержание» необходимо, чтобы в тексте содержалось или слово «канарейки» или слово «содержание». Вывод: чем больше «&», тем меньшее количество страниц найдет поисковик, чем больше «|», тем большее.
На запрос 1 будет найдено больше документов, чем на запрос 2, так как запрос 2 требует расположения слов точно в указанной форме, то есть порядок слов тоже должен сохраняться, следовательно, по второму запросу будет найдено наименьшее количество страниц. По запросу 3 будет найдено меньше документов чем по запросу 4.
Источник