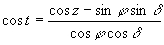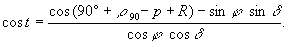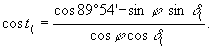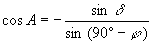Азимут и высота солнца над горизонтом
Вычисление азимута и высоты солнца над горизонтом по заданным координатам и времени наблюдения. Возможно как задание координат вручную, так и выбор значения из справочника городов.
Продолжаем тему, начатую статьей Восход и закат солнца.
На повестке дня вычисление азимута солнца и его высоты над горизонтом в любой момент времени в точке с заданными координатами. Азимут мы откладываем от севера по часовой стрелке.
Алгоритм расчета взят отсюда. Описал его какой-то хороший швед. Он старался как мог, но все равно для стороннего человека ничего не понятно. Например, я могу еще понять, как мы переходим от одной системы координат к другой, но понять, почему долгота перигелия солнца вычисляется как
, где d — количество дней от эпохи J2000 — это уже выше моих сил.
Видимо где-то далеко, в башне из слоновой кости, сидят астрономы, и все эти цифры рассчитывают, а потом все остальные смертные их используют. Может быть какой-нибудь астроном когда-нибудь расскажет о том, как это все происходит; пока же пришлось взять на веру все эти магические цифры и воплотить расчет в жизнь. Очевидно, так делает большинство.
Есть несколько книг, которые обычно рекомендуют людям на форумах, когда не хотят отвечать развернуто, типа, «смотри вон там», и я тоже приведу их здесь:
Jean Meeus. Astronomical algorithms
Peter Duffett-Smith. Practical Astronomy with your calculator.
Как и в случае калькуляторов для расчета времени восхода и захода солнца, ниже представлены два калькулятора — первый берет информацию о координатах и часовом поясе из справочника городов, т. е. остается только выбрать город и ввести время наблюдения; а второй позволяет задать координаты и часовой пояс «вручную». Информацию о городах могут добавлять в справочник зарегистрированные пользователи.
Отрицательная высота над горизонтом соответствует темному времени суток — солнце «под» горизонтом. Пересечение с горизонтом утром происходит примерно на азимуте 90 градусов, из чего можно сделать смелый вывод, что солнце восходит все-таки на востоке.
Paul Schlyter (это швед) утверждает, что ошибка в расчетах не превышает одной угловой минуты для дат в диапазоне 1900 – 2100.
Источник
АЗИМУТ И ВЫСОТА СОЛНЦА НАД ГОРИЗОНТОМ
Высота Солнца над горизонтом – величина непостоянная. В течение дня из-за вращения Земли она проходит путь от 0 до 90 градусов и обратно через фазы восхода, зенита и заката. Но это если наблюдать за нашим светилом из своего города. В масштабах планеты угол, под которым его лучи падают на поверхность Земли в разных регионах, влияют как на климатические условия, так и на продолжительность времени суток.
На ледяных полюсах лучи солнечного света едва касаются нашей планеты. Там очень холодно, а день и ночь длятся по полгода и называются полярными. А вот жаркому экватору достается больше всего солнечного света, который падает туда под прямым углом. В тех краях и климат намного приятнее, и день с ночью имеют практически одинаковую продолжительность. Эти наблюдения подтверждают простой факт: чем выше Солнце, тем больше тепла и света оно дает, а его высота над горизонтом равна углу падения его лучей.
Еще один способ следить за перемещением нашей звезды на небе – это вычисление ее азимута. Сделать это можно с помощью онлайн-калькуляторов для любой точки Земли, например, для Москвы. Понадобятся лишь дата и время. Скажем, в полдень 15-го июня 2018-го года азимут и высота Солнца над горизонтом в Москве составляли 167,29 и 57,08 градуса соответственно.
Вычисление времени восхода и захода в цифровую эру тоже стало делом нескольких кликов. В той же Москве 22-го декабря 2018-го года Солнце встало только в 8:57, а зашло за горизонт уже в 15:58, подарив москвичам лишь семь часов светового дня.
Декабрь — это вообще месяц самых длинных ночей в Северном полушарии, а 22-ое декабря — это дата зимнего солнцестояния, самого короткого дня и самой долгой ночи в году для этой части света. Всему виной опять же высота Солнца над горизонтом. Зимой и особенно в декабре ее значения самые низкие за весь год.
Источник
Горизонтальный угол восхода солнца что это
§ 32. Вычисление моментов времени и азимутов восхода и захода светил
Часовой угол светила определяется из первой формулы (1.37), а именно:
Если какая-нибудь точка небесного свода восходит или заходит, то она находится на горизонте и, следовательно, ее видимое зенитное расстояние z ‘ 90 = 90°. Ее истинное зенитное расстояние z в этот момент вследствие рефракции (см. § 30) будет больше видимого на величину r = 35′. Суточный параллакс понижает светило над горизонтом (см. § 31), т. е. увеличивает видимое зенитное расстояние z ‘ на величину горизонтального параллакса р. Следовательно, истинное зенитное расстояние точки в момент ее восхода или захода
Кроме того, для Солнца и Луны, имеющих заметные размеры, координаты относятся к центру их видимого диска, а восходом (или заходом) этих светил считается момент появления (пли исчезновения) на горизонте верхней точки края диска. Следовательно, истинное зенитное расстояние центра диска этих светил в момент восхода или захода будет больше зенитного расстояния верхней точки края диска на величину видимого углового радиуса R диска. (У Солнца и Луны их видимые угловые радиусы приблизительно одинаковы и в среднем равны 16’.)
Таким образом, при вычислении часового угла светила в момент его восхода и захода в формуле (1.41), в самом общем случае, z = 90° + r 90 — p + R , и она напишется тогда в следующем виде:
По формуле (1.42) часовые углы восхода и захода вычисляются только для Луны. В этом случае R R = 16’, р R = 57’ и r 90 = 35′ . и формула (1.42) принимает вид
При вычислении часовых углов восхода и захода Солнца его горизонтальным параллаксом можно пренебречь, и при R ¤ = 16′ и r 90 = 35′ формула (1.42) принимает вид
Для звезд и планет можно пренебречь также и их видимыми радиусами и вычислять часовые углы восхода и захода по формуле
Наконец, если пренебречь и рефракцией, то часовой угол восхода и захода вычисляется по формуле
Каждое из приведенных уравнений дает два значения часового угла: t 1 = t и t 2 = — t . Положительное значение соответствует заходу, отрицательное — восходу светила. Местное звездное время восхода и захода, согласно формуле (1.15), получается таким:
Затем можно вычислить моменты восхода и захода светила по местному среднему солнечному времени (см. § 23) и по декретному времени (см. § 24).
Если вычисляется восход и заход Солнца, то нет необходимости вычислять звездное время явлений, так как, увеличив часовые углы t 1 и t 2 на 12 h , мы сразу получаем моменты по местному истинному солнечному времени Т ¤ = t ¤ + 12 h . Тогда местное среднее время
где h — уравнение времени (см. § 22), которое берется, так же как a и d Солнца, из Астрономического Ежегодника.
Азимуты точек восхода и захода светил (без учета рефракции, параллакса и углового радиуса) получим, если в первой формуле (1.36) положим z = 90°; тогда cos z = 0 , sin z =1 и
По формуле (1.45) получаем два значения азимута: А 1 = A и A 2 = 360° — A . Первое значение является азимутом точки захода, второе — азимутом точки восхода светила.
Представим теперь формулы (1.45) и (1.44) в виде
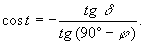
Так как косинус не может быть больше 1, то из этих формул следует, что восход и заход светила возможны только при условии
Источник
Зенитный угол Солнца — Solar zenith angle
Зенитный угол Солнца угла между лучами солнца и вертикальным направлением . Он тесно связан с углом солнечной высоты, который представляет собой угол между солнечными лучами и горизонтальной плоскостью. Поскольку эти два угла дополняют друг друга, косинус одного из них равен синусу другого. Оба они могут быть рассчитаны по одной и той же формуле, используя результаты сферической тригонометрии . В солнечный полдень зенитный угол минимален и равен широте минус угол склонения Солнца . Это основа, на которой древние мореплаватели путешествовали по океанам.
СОДЕРЖАНИЕ
Формула
- θ s <\ displaystyle \ theta _
>
является угол солнечного зенита - α s <\ displaystyle \ alpha _
>— угол солнечной высоты , = 90 ° — α s <\ displaystyle \ alpha _ >θ s <\ displaystyle \ theta _ > - час <\ displaystyle h>— часовой угол по местному солнечному времени .
- δ <\ displaystyle \ delta>текущее склонение Солнца
- Φ <\ displaystyle \ Phi>это местная широта .
Вывод формулы с использованием подсолнечного точечного и векторного анализа
Хотя формулу можно получить, применив закон косинуса к сферическому треугольнику зенит-полюс-Солнце, сферическая тригонометрия — относительно эзотерический предмет.
Вводя координаты подсолнечной точки и используя векторный анализ, формула может быть получена прямо без использования сферической тригонометрии.
В геоцентрической декартовой системе координат, центрированной по центру Земли ( ECEF ), пусть и будут долготой и широтой или координатами подсолнечной точки и точки наблюдателя, затем направленными вверх единичными векторами в двух точках и , находятся ( ϕ s , λ s ) <\ displaystyle (\ phi _ , \ lambda _ )> 
( ϕ о , λ о ) <\ displaystyle (\ phi _ S <\ displaystyle \ mathbf > V о z <\ displaystyle \ mathbf
S знак равно потому что ϕ s потому что λ s я + потому что ϕ s грех λ s j + грех ϕ s k <\ displaystyle \ mathbf = \ cos \ phi _ \ cos \ lambda _ <\ mathbf > + \ cos \ phi _ \ sin \ lambda _ < \ mathbf <\ mathbf , V о z знак равно потому что ϕ о потому что λ о я + потому что ϕ о грех λ о j + грех ϕ о k <\ displaystyle \ mathbf .
где , и — базисные векторы в системе координат ECEF. я <\ displaystyle <\ mathbf >> j <\ displaystyle <\ mathbf k <\ displaystyle <\ mathbf
Теперь косинус зенитного угла Солнца является просто скалярным произведением двух вышеуказанных векторов. θ s <\ displaystyle \ theta _ >
потому что θ s знак равно S ⋅ V о z знак равно грех ϕ о грех ϕ s + потому что ϕ о потому что ϕ s потому что ( λ s — λ о ) <\ displaystyle \ cos \ theta _ = \ mathbf \ cdot \ mathbf + \ cos \ phi _ \ cos (\ lambda _ — \ lambda _ .
Обратите внимание, что это то же самое , что и склонение Солнца, и эквивалентно , где — часовой угол, определенный ранее. Таким образом, приведенный выше формат математически идентичен приведенному ранее. ϕ s <\ displaystyle \ phi _ > δ <\ displaystyle \ delta> λ s — λ о <\ displaystyle \ lambda _ — \ lambda _ — час <\ displaystyle -h> час <\ displaystyle h>
Кроме того, Ref. аналогичным образом вывели формулу для азимутального угла Солнца без использования сферической тригонометрии.
Минимум и максимум
В любом заданном месте в любой заданный день зенитный угол Солнца достигает своего минимума в местный солнечный полдень, когда часовой угол , или , а именно,, или . Если это полярная ночь. θ s <\ displaystyle \ theta _ > θ м я п <\ displaystyle \ theta _ час знак равно 0 <\ displaystyle h = 0> λ s — λ о знак равно 0 <\ displaystyle \ lambda _ — \ lambda _ потому что θ м я п знак равно потому что ( | ϕ о — ϕ s | ) <\ Displaystyle \ соз \ тета _ <мин>= \ соз (| \ фи _ <о>— \ фи _ |)> θ м я п знак равно | ϕ о — ϕ s | <\ displaystyle \ theta _ |> 90^<\circ >>»> θ м я п > 90 ∘ <\ displaystyle \ theta _ 90 ^ <\ circ>>»>
И в любом месте в любой день зенитный угол Солнца достигает своего максимума в местную полночь, когда часовой угол , или , а именно,, или . Если это полярный день. θ s <\ displaystyle \ theta _ > θ м а Икс <\ displaystyle \ theta _ час знак равно — 180 ∘ <\ displaystyle h = -180 ^ <\ circ>> λ s — λ о знак равно — 180 ∘ <\ displaystyle \ lambda _ — \ lambda _ потому что θ м а Икс знак равно потому что ( 180 ∘ — | ϕ о + ϕ s | ) <\ displaystyle \ cos \ theta _ |)> θ м а Икс знак равно 180 ∘ — | ϕ о + ϕ s | <\ displaystyle \ theta _ |> θ м а Икс 90 ∘ <\ displaystyle \ theta _
Предостережения
Рассчитанные значения являются приблизительными из-за различия между общей / геодезической широтой и геоцентрической широтой . Однако эти два значения отличаются менее чем на 12 угловых минут , что меньше видимого углового радиуса Солнца.
Формула также не учитывает влияние атмосферной рефракции .
Приложения
Восход закат
Закат и восход солнца происходят (приблизительно), когда зенитный угол равен 90 °, где часовой угол h 0 удовлетворяет
потому что час 0 знак равно — загар Φ загар δ . <\ displaystyle \ cos h_ <0>= — \ tan \ Phi \ tan \ delta.>
Точное время заката и восхода происходит тогда, когда верхняя часть Солнца, преломленная атмосферой, оказывается на горизонте.
Альбедо
Средневзвешенный зенитный угол, используемый при вычислении местного альбедо Земли , определяется выражением
потому что θ s ¯ знак равно ∫ — час 0 час 0 Q потому что θ s d час ∫ — час 0 час 0 Q d час <\ displaystyle <\ overline <\ cos \ theta _ >> = <\ frac <\ int _ <- h_ <0>> ^ <\ текст
Резюме специальных углов
Например, угол возвышения Солнца равен:
- 90 °, если вы находитесь на экваторе, в день равноденствия, в двенадцатый солнечный час.
- около 0 ° на закате или на восходе
- от -90 ° до 0 ° ночью (полночь)
Дан точный расчет положения Солнца . Другие приближения существуют в другом месте.
Источник