Азимут и высота солнца над горизонтом
Вычисление азимута и высоты солнца над горизонтом по заданным координатам и времени наблюдения. Возможно как задание координат вручную, так и выбор значения из справочника городов.
Продолжаем тему, начатую статьей Восход и закат солнца.
На повестке дня вычисление азимута солнца и его высоты над горизонтом в любой момент времени в точке с заданными координатами. Азимут мы откладываем от севера по часовой стрелке.
Алгоритм расчета взят отсюда. Описал его какой-то хороший швед. Он старался как мог, но все равно для стороннего человека ничего не понятно. Например, я могу еще понять, как мы переходим от одной системы координат к другой, но понять, почему долгота перигелия солнца вычисляется как
, где d — количество дней от эпохи J2000 — это уже выше моих сил.
Видимо где-то далеко, в башне из слоновой кости, сидят астрономы, и все эти цифры рассчитывают, а потом все остальные смертные их используют. Может быть какой-нибудь астроном когда-нибудь расскажет о том, как это все происходит; пока же пришлось взять на веру все эти магические цифры и воплотить расчет в жизнь. Очевидно, так делает большинство.
Есть несколько книг, которые обычно рекомендуют людям на форумах, когда не хотят отвечать развернуто, типа, «смотри вон там», и я тоже приведу их здесь:
Jean Meeus. Astronomical algorithms
Peter Duffett-Smith. Practical Astronomy with your calculator.
Как и в случае калькуляторов для расчета времени восхода и захода солнца, ниже представлены два калькулятора — первый берет информацию о координатах и часовом поясе из справочника городов, т. е. остается только выбрать город и ввести время наблюдения; а второй позволяет задать координаты и часовой пояс «вручную». Информацию о городах могут добавлять в справочник зарегистрированные пользователи.
Отрицательная высота над горизонтом соответствует темному времени суток — солнце «под» горизонтом. Пересечение с горизонтом утром происходит примерно на азимуте 90 градусов, из чего можно сделать смелый вывод, что солнце восходит все-таки на востоке.
Paul Schlyter (это швед) утверждает, что ошибка в расчетах не превышает одной угловой минуты для дат в диапазоне 1900 – 2100.
Источник
Исходные данные и результаты расчета высоты Солнца
| Задача | Исходные данные | Результаты расчета | Схема | ||
| № | позиция | q | Ш | h0 | h· |
  1 1 | а | 113,5° летнее солнцестояние 22.06 | экватор | 113,5 | -66,5 |
| б | полюс | 23,5 | 23,5 | ||
| в | Харьков | 63,5 | -16,5 | ||
   2 2 | а | 66,5° зимнее солнцестояние | экватор | 66,5 | -113,5 |
| б | полюс | -23,5 | -23,5 | ||
| в | Харьков | -63,5 | |||
 3 3 | а | 90° равноденствие | экватор | -90 | |
| б | полюс | ||||
| в | Харьков | -40 |
Сопоставляя полученные данные с рассчитанными ранее, а так же имеющимися в литературе, можно заключить, что зависимости (84) и (85) верны. Указанные величины позволяют определить высоту солнца в полночь и полдень, а так же определить точки его восхода и заката. Они будут на пересечении линий горизонта и линии, соединяющей Солнце в двух противоположных точках. Однако, всего этого не достаточно для определения траектории Солнца. Здесь необходимо знать высоту Солнца не только в полдень (полночь), но и любое время суток.
Для решения задачи возьмем произвольную широту, пусть это будет лето, и изобразим некоторую экспозицию (рисунок 52).
Рисунок 52 – Схема к расчету высоты Солнца
На рисунке изображена траектория движения Солнца в один из летних месяцев в северном полушарии. Признаки: Солнце в полдень сориентировано точно на юг по отношению к наблюдателю Т, восходит в точке В (восход) слева, если смотреть на юг, и заходит на западе справа. Определим высоту Солнца в полдень H1 и условную высоту солнца Н2 в полночь, зная соответствующие высоты солнца h0 и h·, и приняв радиус полусферы Rп равным 1. Тогда:
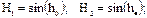
Подставляя в полученные выражения значения h0 и h· из зависимостей (60) и (61) получим:
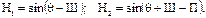
Плоскость, в которой вращается Солнце, как бы поднята над плоскостью горизонта, а ее центр Т является центром основания конуса с вершиной в точке Т. Образующей этого конуса является радиус полусферы единичного радиуса. При этом телесный угол у вершины конуса зависит от угла q, то есть от времени года. С изменением широты, конус будет поворачиваться вокруг точки Т меридиальной плоскости, оставаясь неизменным.
Для большей наглядности разрежем экспозицию меридиальной плоскостью (меридиальная плоскость проходит по линии север – юг), как показано на рисунке 53.
Рисунок 53 – Схема к расчету траектории Солнца
Так как основанием конуса является окружность с радиусом R, причем солнце делает полный оборот по ней ровно за 24 часа с постоянной скоростью, то ее можно разбить на часовые секторы с началом отсчета от точки ПН (полночь – 0 часов). В момент полудня (12 часов), т.е. пройдя половину круга, солнце достигает наибольшей высоты.
Но так как общепринято отсчитывать азимут от южного направления за часовой стрелкой, то и мы будем придерживаться этого правила, то есть угол А° будем отсчитывать за часовой стрелкой. Зная радиус основания конуса и угол А° найдем проекцию r линии, соединяющей точки Т1 и С (см. рисунок 70), на линию пересечения меридиальной плоскости и основания конуса:
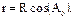
Подставив значение r, получим:
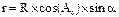
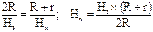
Подставляя в выражение (89) значение r из (85), и учитывая, что Н3=Н1-Н2 найдем:
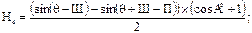
С учетом выражения (89) и зная, что h=H4–H2 , получим:
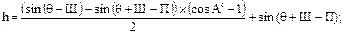
По зависимости (93) можно рассчитать высоту солнца над горизонтом для любого времени суток и периода года. Для определения угловой высоты Солнца можно воспользоваться зависимостью:
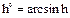
1. Определить высоту стояния Солнца в 12 часов дня на экваторе в период летнего солнцестояния.
Решение: Определим параметры, входящие в выражение (94).
Угол q определим по выражению (69) или по графику (см. рисунок 69). q = 113,5°. Широта экватора Ш = 0. Для времени 12 часов угол А0 = 0. Подставляя полученные значения в выражение (94) получим:
2. Определить высоту стояния Солнца в 0 часов ночи на экваторе в период летнего солнцестояния.
Решение: см. пример 1. q = 113,5°; Ш = 0°; А0 = 180°.
Подставляя полученные значения в выражение (94) получим:
3. Определить высоту стояния Солнца в 18 часов дня на широте экватора в период летнего солнцестояния.
Решение: см. пример 1. q = 113,5°; Ш = 0°; А0 = 90°.
Подставляя полученные значения в выражение (94) получим:
4. Определить высоту стояния Солнца в полдень на Северном полюсе в период летнего солнцестояния.
Решение: см. пример 1 и 2. q = 113,5°; Ш = 90°; А0 = 0°.
Подставляя полученные значения в выражение (94) получим:
5. Определить высоту стояния Солнца в полночь на Северном полюсе в период летнего солнцестояния.
Решение: см. приведенные выше примеры. q = 113,5°; Ш = 90°; А0 = 180°.
Подставляя полученные значения в выражение (94) получим:
6. Определить высоту стояния Солнца в 6 часов утра на Северном полюсе в период летнего солнцестояния.
Решение: см. приведенные выше примеры. q = 113,5°; Ш = 90°; А0 = 180°.
Подставляя полученные значения в выражение (94) получим:
7. Определить время восхода и захода солнца в период летнего солнцестояния в городе Харькове.
Решение: q = 113,5°; Ш = 50°. Время восхода и захода солнца будет при h = 0.
Подставляя полученные значения в выражение (94) получим:
Для того, чтобы Солнце от наиболее высокой точки в полдень опустилось до горизонта, оно должно сместиться по отношению к точке Т1 на угол А°, то есть на 119,5°. Известно, что за 1 час Солнце смещается по отношению к точке Т на 15°. С учетом этого определим величину угла в часах:
Это значит, что солнце от полудня до заката пройдет 7,98 часа, следовательно, закат наступит в 12 + 7,98 = 19,98 часа = 19 ч. 59 мин.
Известно, что полудуги, которые описывает Солнце от восхода до заката, и от полудня до заката, симметричны. Тогда восход Солнца наступит в 12 — 7,98 = 4,02 часа = 4 ч. 1 мин.
Не следует путать полученное местное время с принятым поясным московским.
8. Определить время восхода и заката солнца в период летнего солнцестояния в городе Москве.
Решение: по аналоги с задачей 7 определим А° = 128,12°. Следовательно, от полудня до заката пройдет 8,54часа.
Тогда восход в Москве наступит в 12 — 8,54 = 3,48 часа = 3 ч. 29 мин.
Закат наступит соответственно в 12 + 8,54 = 20,54 часа = 20 ч. 54 мин.
Сопоставив примеры 7 и 8, увидим, что восход солнца в г. Харьков будет на 32 минуты запаздывать по сравнению с восходом в Москве, не смотря на то, что оба города находятся в одном часовом поясе и, более того, почти на одном меридиане. В этой связи следует подчеркнуть, что когда мы рассуждали о местном времени, то их не следовало смешивать с восходом и закатом солнца, так как они зависят не только от меридиана, но и от широты.
9. Определить, на какой высоте будет находится солнце в г. Харькове в 15 часов 20 февраля (год не високосный).
Решение: Определим угол q из зависимости (94):
Зная, что год имеет 365 дней (не високосный), а угол b за год изменяется от 0° (летнее солнцестояние – 22 июня) до 360°, то за одни сутки земля сместиться от некоторого положения на:
Посчитаем теперь, сколько дней пройдет от 22 июня (за начало отсчета берем начало суток) до 20 февраля. Общее количество дней будет равно 242. Тогда угол b будет равен:
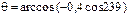
Теперь мы знаем уже два параметра: угол q и широту г. Харькова. Найдем третий параметр: угол А° по графику (см. рисунок 69). В 15 часов он будет составлять 45°. Подставим полученные данные в выражение (68) и найдем h.
Источник
 germanrus
germanrus
Привет всем
Солнце над плоской землей, ходит по сложной спиралевидной орбите, меняя каждый день не только высоту и длину своей окружности но и скорость.
Высоту Солнца на ПЗ лучше всего мерить 2 раза в год, это 22 декабря и 22 июня, именно в эти дни можно сделать самые точные расчеты.
Расстояние от Берлина до Южного тропика, равно 8.500 км. (катет B) а угол отбрасываемой тени равен 14,5 градусам. Нужно найти катет А. (т.е. Высоту)
Для расчета воспользуемся калькулятором
Расстояние от Берлина до Северного тропика 3.200 км. (Катет В)
Воспользуемся калькулятором и получаем высоту катета „А“ = 5.893,6 км.
3.695,3 км / 180 дней = 20,53 км в день, на такое расстояние солнце опускается зимой а летом поднимается, за один оборот по своей орбите, т.е. шаг спиральной орбиты Солнца по вертикале равен 20,53 км.
Recent Posts from This Journal
 Глобальная катастрофа 23 Сентября 1692 года
Глобальная катастрофа 23 Сентября 1692 года
Фризские источники, с точностью до часа говорят когда произошла катастрофа. Глобальная катастрофа произошла 23 Сентября 1692 года после полудня. В…
 в Якутии нашли голову волка
в Якутии нашли голову волка
P.S. вот наглядный пример как делается история, сказали 40.000 лет и все тут, верьте. А то что этот волк еще спокойно жил 300 лет назад, до…
 Тайна подземелий Капитолия
Тайна подземелий Капитолия
Так вы уже определитесь, лучи в земной атмосфере распространяются прямолинейно или по сложным криволинейным путям, обусловленным хитроумными законами «преломления» над и под куполом, которые обеспечивают закручивание небесной сферы по часовой стрелке в южном полушарии и т.п.
К тому же использование количества точек визирования солнца больше двух тут же ломает все ваши построения. Ибо практические наблюдения уже из трех мест никак не захотят собрать все лучи в одну точку условного положения Солнца.
Edited at 2019-11-12 10:48 pm (UTC)
Расстояние от земли до солнца над экватором каждый может посчитать за пару минут без всяких измерений .И то с очень высокой точностью.
Два раза в год солнце, двигаясь из северного тропика (23,5 гр) к южному (-23.5 гр) ,пересекает экватор.Вы удивитесь,но и на шаро-верной модели тоже также..просто тут теперь специфически кувыркается земля,как волчек на последнем издыхании(прецессия).
Так вот.
Тот у кого есть спутниковая антенна знает,что во время нахождения солнца над экватором спутниковая антенна,геостационарный спутник и солнце
выстраивается в одну линию и на телевизоре в это время на несколько секунд полностью пропадает сигнал.Это явление называется солнечная интерференция или засветка.
Теперь у вас есть прямоугольный треугольник с известными
углами 90 град на экваторе и угол подъема антенны, припустим @.
Один катет нам тоже известен-это расстояние от
вашей антенны к экватору(в помощь вам гугл).По формуле из тригонометрии вы, используя инженерный калькулятор, вычисляете высоту солнца над экватором на раз,два,три..т.е. расстояние от антенны к экватору умножаете на тангенс
угла подъема антенны @,который вы можете узнать непосредственно измерив вассервагой(уровнем) или из программы настройки
спутниковой антенны (можно скачать в интернете к примеру Satellite-Antenna-Alignment-install-2.36.8.r ar) ,
выставив в ней ваши географические координаты-и тут вам гугл в помощь..и название спутника..к примеру, где вы смотрите пакет НТВ+ и Триколор — 36 град.
Приблизительно у вас должно выйти около 3000 км..
Данное явление солнечной интерференции напрочь хоронит геостационарные спутники 36 000 км как на шарообразной модели (ШЗ) так и на модели плоской земли(ПЗ) ,поскольку на одной линии может находиться солнце,спутник и антенна,которая находится на экваторе,но никак не в северной части планеты,где мы смотрим пакет НТВ+ и Триколор для ШЗ, и в одной точке не
может находится одновременно солнце и спутник для ПЗ..))
Ну и естественно разоблачает и космический обман.
Ваш пост пустышка.
Я некоторое время анализировал ваш пост, в итоге пришел к выводу, что ваше «доказательство» ничего не доказывает и вообще ничего не значит. Я думаю, очевидно даже вам, что ваша рейка может отбрасывать такую тень и в гелиоцентрической системе из-за наклона оси вращения земли. Конечно, длинна тени на дуге должна быть больше чем на плоской поверхности, но, в случае шарообразной земли, ваша рейка ничтожно мала по сравнению с радиусом земли. Поэтому, что линейкой измерять, что через геометрические теоремы, длинна тени будет примерно одинакова в обоих случаях(погрешность в очень много нулей после запятой).
Насчет вашего комментария про солнечную интерференцию — бредятина, противоречит даже вашим моделям, которые нарисованы на ваших картинках. Оно вообще всему противоречит, потому что это — бредятина. Если солнце будет находиться над экватором, то слабый сигнал будут ощущать лишь те тарелки, которые находятся вблизи или на экваторе. Да даже если это не так, как вы собираетесь искать расстояние между землей и солнцем в треугольнике, в который это солнце даже не входит? Ведь тарелка направленна на спутник, а не на солнце. К слову, если считать расстояние между землей и спутником в геостационарной орбите, в гелиоцентрической системе отсчета, то все встанет на свои места. Поэтому ваш расчет высоты спутника тоже ничего не значит.
Источник
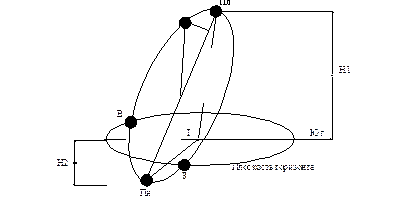

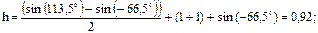
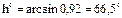
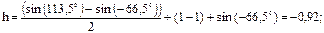

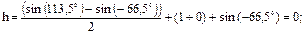
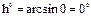





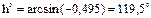
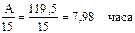

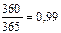
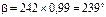
 germanrus
germanrus 








 Глобальная катастрофа 23 Сентября 1692 года
Глобальная катастрофа 23 Сентября 1692 года  в Якутии нашли голову волка
в Якутии нашли голову волка  Тайна подземелий Капитолия
Тайна подземелий Капитолия