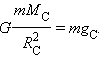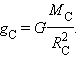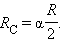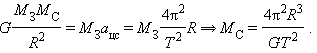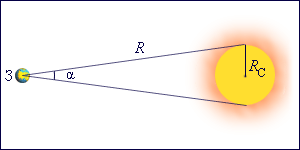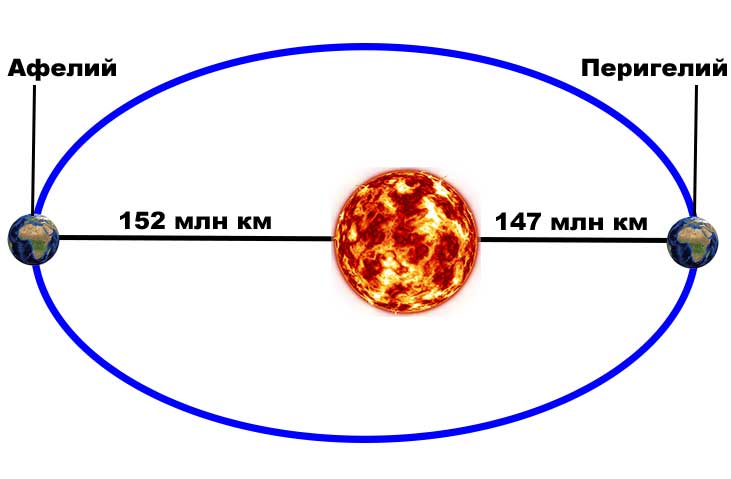
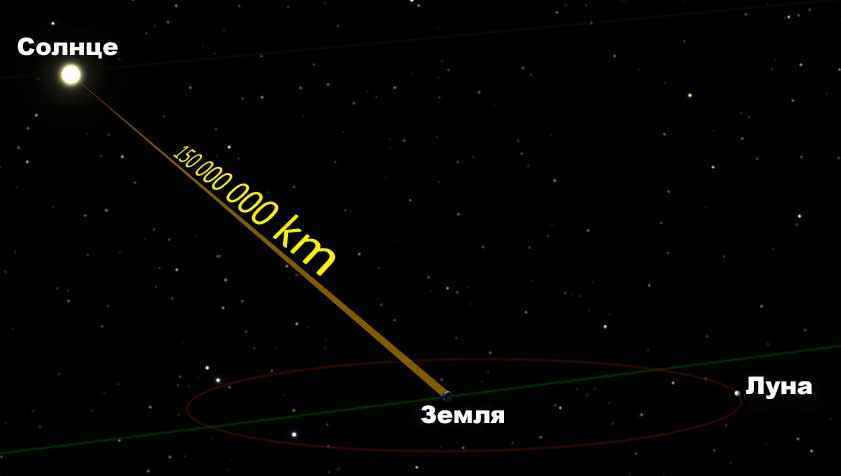
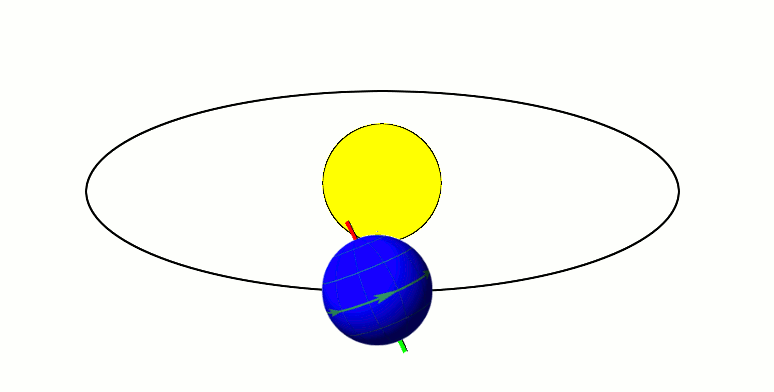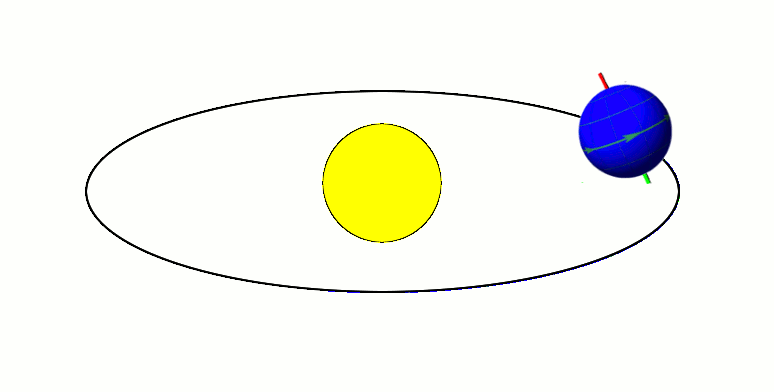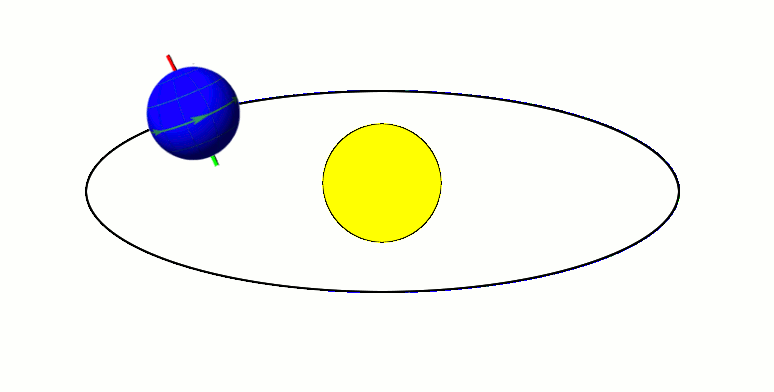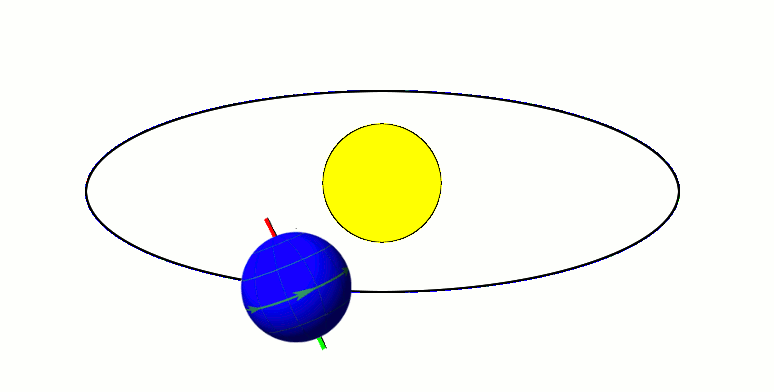
Массу Солнца можно определить, применив второй закон Ньютона к орбитальному движению Земли:

Подставляя выражения для и в формулу для ускорения свободного падения , получим:

Источник

По какой орбите Земля движется вокруг Солнца?

Из школьного курса всем известно, что Земля вращается относительно Солнца. Орбита – это траектория движения нашей планеты вокруг звезды. Есть ли у неё какие-нибудь примечательные особенности?

Форма траектории

Долгое время астрономы полагали, что орбиты небесных тел – это окружности. Однако Иоганн Кеплер установил, что на самом деле планеты, в том числе Земля, двигаются по эллиптической траектории, причем Солнце находится в одном из фокусов этого эллипса.

У эллипса, который выглядит как сплюснутая окружность, есть такой параметр, как эксцентриситет. Он определяет, насколько близка его форма к окружности. Эксцентриситет может принимать значение от нуля до единицы. Если он равен нулю, то орбита становится идеальным кругом, в центре которого расположена звезда. Земной эксцентриситет равен 0,0167, то есть наша орбита очень близка к круговой.

Точка, в которой небесное тело максимально удалено от своего светила, называется апоцентром, а ближайшая точка именуется перицентром. Применительно к планетам Солнечной системы также используются термины афелий и перигелий. Когда Земля находится в афелий, расстояние от неё до Солнца составляет 152 млн км, а в перигелий оно сокращается до 147 млн км.

Столь незначительное изменение радиуса земной орбиты очень важно для жизни на планете, так как оно позволяет поддерживать стабильное значение средней температуры на ней. Для сравнения – радиус орбиты Меркурия меняется от 46 до 70 млн км, что соответствует значению эксцентриситета 0,2.

Расстояние от Земли до Солнца

Средний радиус земной орбиты, равный 150 млн км, принят за одну астрономическую единицу – единицу измерения расстояний в космическом пространстве. Исторически ее удобно было использовать при описании Солнечной системы.

Дело в том, что определить относительные расстояния в ней (например, вычислить, что радиус венерианской орбиты в 1,4 раза меньше радиуса земной), значительно проще, чем рассчитать абсолютные. Поэтому астрономы приняли расстояние между Землей и Солнцем за условную единицу и через нее выражали все остальные линейные размеры в нашей планетной системе. Лишь в 1672 году с помощью измерения параллакса Марса итальянцу Джованни Кассини удалось впервые оценить радиус земной орбиты в 140 млн км.

Более точное значение астрономической единицы удалось получить методом радиолокации Венеры советским астрономам в 1961 году. Они получили значение 149 599 300±2000 км.

Скорость движения Земли

Общая протяженность орбиты нашей планеты составляет 940 млн км, которые Земля преодолевает за 365,25 дня, именно поэтому каждый четвертый год делают високосным, добавляя к нему 29 февраля. При этом небесные тела движутся по орбите с неравномерной скоростью. Быстрее всего планеты движутся в перицентре, а медленней всего в апоцентре. Земля оказывается в афелие 3 июля и замедляется в этот день до 29,2 км/с. 3 января наша планета достигает перигелия, разгоняясь да 30,2 км/с.

Плоскость орбиты

Орбита каждого небесного тела – это плоская фигура, то есть все ее точки лежат в одной плоскости. Плоскость земной орбиты называется эклиптикой. Интересно, что орбиты всех известных нам планет Солнечной системы почти лежат в эклиптике. Ось вращения Земли вокруг собственной оси наклонена под углом 23° к эклиптике, следствием этого наклона является неравномерный нагрев Северного и Южного полушария на разных участках орбиты, из-за чего возникает сезонность погоды. Когда выше экватора лето, ниже него – зима, и наоборот.

Солнце также вращается вокруг собственной оси, причем все планеты вращаются в ту же сторону, что и светило. Это является косвенным доказательством того, что когда-то вещество, из которого состоят все планеты и наша звезда, было единым газопылевым облаком, от которого отделился строительный материал для планет. Однако есть одна аномалия, объяснение которой до сих пор не найдено. Дело в том, что само Солнце вращается не в эклиптике, а с отклонением от неё на шесть градусов. Астрономы предполагают, что это может служить косвенным доказательством того, что в нашей системе есть ещё неоткрытые планеты, которые также двигаются не в эклиптике, и своим гравитационным воздействием раскачивают ось вращения Солнца.

Отклонение орбиты от идеальной формы

Идея Кеплера о том, что орбиты небесных тел – это эллипсы, очень хорошо описывала поведение планет с точки зрения наблюдателей XVII века, однако с повышением точности измерений стали обнаруживаться отклонения от законов Кеплера. Дело в том, что предложенная немецким астрономом математическая модель была построена на двух упрощениях:

• масса планеты пренебрежимо мала относительно массы звезды;
• учитывается только взаимное влияние сил тяжести двух тел, звезды и планеты, а влияние третьих тел (других планет) не учитывается.

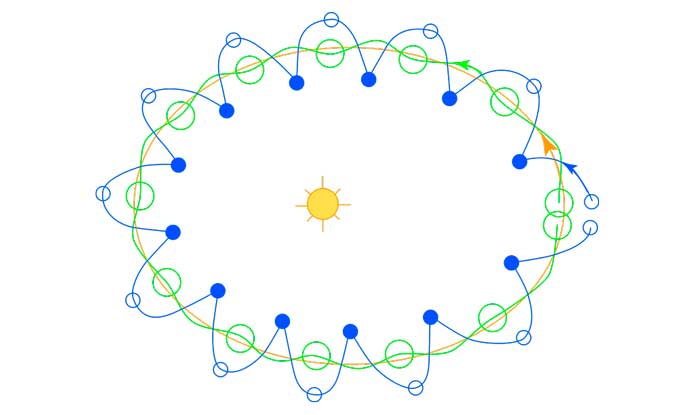
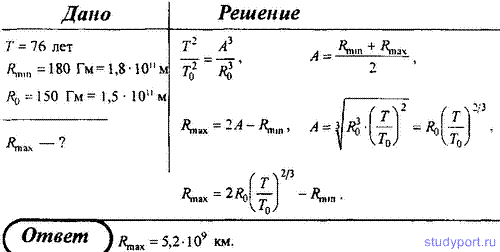
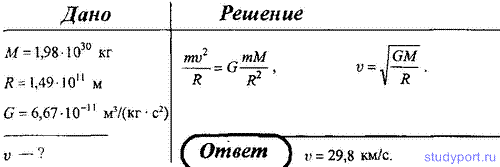
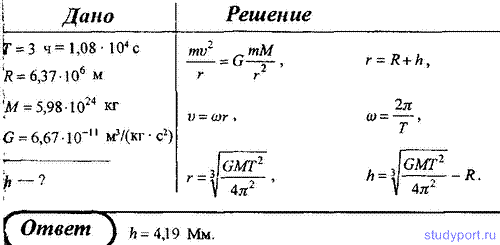
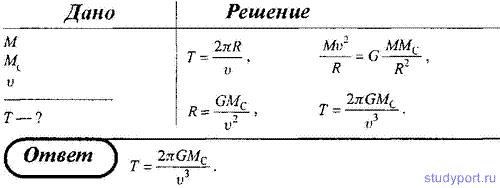
Естественно, в реальности всё сложнее. На самом деле правильнее считать, что не Земля вращается вокруг Солнца, а оба объекта вращаются относительно общего центра масс, который называется барицентром. Но в силу огромной массы звезды барицентр находится внутри неё.

Точные астрономические измерения показывают, что в наше время расстояние между Землей и Солнцем медленно увеличивается со скоростью 15 см в год. Однако это не значит, что наша планета будет постоянно удаляться от светила, периоды удаления могут чередоваться с периодами сближения.

Например, астроном Милутин Миланкович обнаружил, что эксцентриситет земной орбиты не постоянен, а циклически изменяется. Длительность таких циклов составляет около 100 тысяч лет, в течение которых эксцентриситет меняется от 0,005 до 0,05. Именно эти колебания являются причиной ледниковых периодов.

Устойчива ли орбита Земли?

По законам Кеплера планеты могут вращаться вокруг звезды бесконечно долго, однако из-за отклонений от этих законов возможен вариант и неустойчивости, когда планеты покидают свою орбиту или, наоборот, падают на светило. Аналитически рассчитать это невозможно, поэтому приходиться применять компьютерное моделирование.

Проведенные расчеты не позволяют однозначно предсказать судьбу планет Солнечной системы. В некоторых моделях Меркурий либо падает на Солнце, либо сталкивается с Венерой или Землей. Также он может спровоцировать столкновение других планет. Но произойдет это через миллиарды лет.

Источник

Тяготение

171. Определить период обращения вокруг Солнца искусственной планеты, если известно, что большая полуось ее эллиптической орбиты больше на 10 7 км большой полуоси земной орбиты.

172. Период обращения кометы Галлея вокруг Солнце T = 76 лет. Минимальное расстояние, на котором она проходит от Солнца составляет 180 Гм. Определить максимальное расстояние, на которое комета Галлея удаляется от Солнца. Радиус орбиты Земли принять равным R₀ = 150 Гм.

173. Считая орбиту Земли круговой, определить линейную скорость v движения Земли вокруг Солнца.

174. Период обращения искусственного спутника Земли составляет 3 ч. Считая его орбиту круглой, определить, на какой высоте от поверхности Земли находится спутник.

175. Планета массой М движется по окружности вокруг Солнца со скоростью v (относительно гелиоцентрической системы отсчета). Определить период обращения этой планеты вокруг Солнца.

176. Определите, во сколько раз сила притяжения на Земле больше силы притяжения на Марсе, если радиус Марса составляет 0,53 радиуса Земли, а масса Марса — 0,11 массы Земли.

177. Определить среднюю плотность Земли, считая известными гравитационную постоянную, радиус Земли и ускорение свободного падения на Земле.

178. Две материальные точки массами m₁ и m₂ расположены друг от друга на расстоянии R. Определить угловую скорость вращения, с которой они должны вращаться вокруг общего центра масс, чтобы расстояние между ними осталось постоянным.

179. Два одинаковых однородных шара из одинакового материала, соприкасаясь друг с другом, притягиваются. Определить, как изменится сила притяжения, если массу шаров увеличить в n = 3 раза за счет увеличения их размеров.

180. Определите высоту, на которой ускорение свободного падения составляет 25% от ускорения свободного падения на поверхности Земли.

181. Считая плотность Земли постоянной, определите глубину, на которой ускорение свободного падения составляет 25% от ускорения свободного падения на поверхности Земли.

182. На какой высоте h ускорение свободного падения вдвое меньше его значения на поверхности Земли.

183. Стационарным искусственным спутником Земли называется спутник, находящийся постоянно над оной и той же точкой экватора. Определить расстояние такого спутник до центра Земли.

184. На экваторе некоторой планеты (плотность планеты ρ = 3 г/см 3 ) тела весят в два раза меньше, чем на полюсе. Определить период обращения планеты вокруг собственной оси.

185. Принимая, что радиус Земли известен, определить, на какой высоте h над поверхностью Земли напряженность поля тяготения равна 4,9 Н/кг.

186. Определить, в какой точке (считая от Земли) на прямой, соединяющей центры Земли и Луны, напряженность поля тяготения равна нулю. Расстояние между центрами Земли и Луны равно R, масса Земли в 81 раз больше массы Луны.

187. Имеется тонкий однородный стержень массой m и длиной l. Для точки, находящейся на одной прямой со стержнем на расстоянии a от его ближайшего конца, определить: 1) потенциал гравитационного поля стержня; 2) напряженность его гравитационного поля.

188. Тонкий однородный диск радиусом R имеет массу m. Определить в точке A, расположенной на оси диска на расстоянии h от него: 1) потенциал гравитационного поля; 2) напряженность гравитационного поля.

189. Два тела массой m, находящегося в гравитационном поле Земли над ее поверхностью, выведите зависимость потенциальной энергии тела от расстояния до центра Земли. Считая известными радиусы Земли R₀ и ускорение свободного падения g на поверхности Земли.

190. Как известно, искусственный спутник Земли движется вокруг нее по круговой орбите. Определить, во сколько раз гравитационная потенциальная энергия спутника больше его кинетической энергии.

191. Два алюминиевых шарика (ρ = 2,7 г/см3) радиусом r₁ = 3 см и r₂ = 5 см соприкасаются друг с другом. Определить потенциальную энергию их гравитационного взаимодействия.

Ошибка в тексте? Выдели её мышкой и нажми

Остались рефераты, курсовые, презентации? Поделись с нами — загрузи их здесь!

Источник