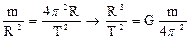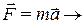Вопрос про гравитацию.
Вопрос — замечательный, пожалуй один из лучших, что я видел на проекте.
В нем содержится крупный подвох. Уже можно начинать с того, что 3-й закон Кеплера (на который многие ссылаются) в такой системе, мягко выражаясь, будет неточен. Даже в Википедии (опять на которую ссылаются) есть примечание о неточности этого закона и появляющейся зависимости от МАСС.
И еще одно обстоятельство! Центр масс такой системы существенно сместится и окажется уже за пределами Земли. В уме прикинул, может промахнулся, потом точнее рассчитаю, но где-то на 2000-3000 км от поверхности Земля. Если «в лоб» применять 3-й закон, получится рассинхронизация, т. е. периоды обращения Земли и Луны будут «как бы» вращаться вокруг общего центра масс с разными периодами. Глупо, не правда ли?
Ну и перед тем как уйти в рассчет, замечу, что «по той же самой орбите» — термин, совершенно некорректный в такой постановке задачи. В лучшем случае — на такой же орбите относительно центра масс.
Итак, ухожу в рассчеты, дополню ответ позже (если получится) .
——
Дополняю (из чего исходить, решая) :
Еще Ньютон показал, что третий закон Кеплера не совсем точен — в действительности в него входит и масса планеты:
, где M – масса Солнца, m1 и m2 – массы планет.
T1 и T2 — периоды обращения двух планет вокруг Солнца, а a1 и a2 — длины больших полуосей их орбит.
Поскольку движение и масса оказались связаны, эту комбинацию гармонического закона Кеплера и закона тяготения Ньютона используют для определения массы планет и спутников, если известны их орбиты и орбитальные периоды.
Понятно если соотношение масс велико, то роль поправки исчезающе незначительна, как и в случае спутник-земля или в случае со спутниками Юпитера. Но если брать, например, Ваш предудущий вопрос о «Луне в два раза тяжелей», то там это проявится. Там даже общий центр масс «улетит» за пределы Земли. Будет «двойная планета».
Источник
Центральные



«Гравитация не может отвечать за тех, кого любовь сбивает с ног».
Закон всемирного тяготения ничего не говорит о том, почему силы тяготения именно такие, как они возникают и передаются в пространстве.
Границы применимости закона всемирного тяготения (общая теория относительности): Закон всемирного тяготения верен до тех пор, пока расстояние между телами много больше гравитационного радиуса притягивающего тела r >> Rгр = 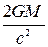
IV.Задачи:
1. В одной из установок опытной проверки закона всемирного тяготения сила притяжения между свинцовым шаром массой 5 кг и шариком массой 10 г на расстоянии 7 см была равна 6,8·10 -10 Н. Чему равна, на основании этих данных, гравитационная постоянная?
2. Определите силу тяготения между Луной и Землей, находящимися на расстоянии 365 000 км, если масса Луны 7,3·10 22 кг, и она движется вокруг Земли со скоростью 1 км/c.
3. Во сколько раз уменьшится сила тяготения между однородным шаром и материальной точкой, соприкасающейся с шаром, если материальную точку удалить от поверхности шара на расстояние, равное двум диаметрам шара?
4. Имеется шар массой М и радиусом R, и материальная точка массой m. Во сколько раз уменьшится сила тяготения между ними, если в шаре сделать сферическую полость радиусом R/2. Центры шара и полости совпадают.
1. Во сколько раз изменится сила тяготения между двумя телами, если массу одного из них увеличить в два раза, а расстояние между ними уменьшить в два раза?
2. Два стальных шарика положены на стол вплотную друг к другу. Как определить силу притяжения между ними?
3. Если бы масса Луны была вдвое больше и Луна обращалась бы по той же орбите, то каков бы был период ее обращения?
4. Может ли при сближении двух тел, сила гравитационного притяжения между ними уменьшатся?
5. Почему в периоды новолуний и полнолуний приливы достигают максимальной высоты?
6. Почему в невесомости у космонавтов кровь от ног приливает к голове?
7. Земля сильнее притягивает к себе Луну, чем Луна Землю, иначе Земля была бы спутником Луны. Так ли это?
8. Почему закон всемирного тяготения верен лишь в трехмерном пространстве?
Дополнительный материал: Как из третьего закона Кеплера получить закон всемирного тяготения? А наоборот?
а = G
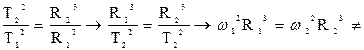
Предположим теперь, что сила взаимодействия планет с Солнцем пропорциональна некоторой степени расстояния: F
R n → a = С · R n , но а = ω 2 R и ω 2 = С · R n-1 , и ω 2 R 3 = C · R n-1 R 3 = C · R n+2 → произведение не зависит от R при n = — 2.
ω 2 R 3 = С, а С = GM; – предположение Ньютона, тогда а = G 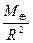
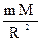
V.
1. Оцените силу, действующую на Землю со стороны одной из ближайших к нам звезд (α-Центавра).
2. Найдите точку равновесия между Землей и Луной.
3. Можно ли по максимальной высоте прибывающей во время прилива воды рассчитать массу Луны?
4. Используя закон всемирного тяготения, выведите для планет одной системы формулу третьего закона Кеплера. Считайте орбиты планет окружностями.
Все тела тяготеют к каждой отдельной планете и веса тел на всякой отдельной планете при одинаковых расстояниях от ее центра пропорциональны массам этих планет.
Урок 34/14. СИЛА ТЯЖЕСТИ
Цель урока: дать представление о силе тяжести, гравитационной массе тела и способе ее измерения. Подтвердить факт равенства гравитационной и инертной масс.
Тип урока: комбинированный.
Оборудование: динамометр, груз.
План урока: 1. Вступительная часть 1-2 мин.
3. Объяснение 20 мин.
4. Закрепление 10 мин.
5. Задание на дом 2-3 мин.
II. Опрос фундаментальный: 1. Сила всемирного тяготения. 2. Гравитационная постоянная.
1. Определите силу, под действием которой Земля движется вокруг Солнца. Орбиту Земли принять круговой. Масса Солнца 2·10 30 кг, масса Земли 6·10 24 кг, расстояние от Земли до Солнца 15·10 10 м.
2. На сколько процентов уменьшится сила тяготения между двумя одинаковыми однородными шарами, если вначале шары соприкасались друг с другом, а затем один из шаров отодвинули на расстояние, равное трем радиусам шаров?

3. Космонавт высадился на Луну. Его притягивает и Луна, и Земля. Во сколько раз сила притяжения космонавта к Луне больше, чем к Земле?
4. К грузу массой 7 кг подвешен на нерастяжимой веревке груз массой 5 кг. Масса веревки 4 кг, система расположена вертикально. К верхнему грузу приложена направленная вверх сила 188,8 Н. Найти силу натяжения в верхнем и в нижнем конце веревки.
|
ΙΙΙ. Сила тяжести ( 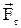
h Fт = G 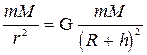
r Вблизи земной поверхности h -12 . Зависимость ускорения свободного паления от широты места наблюдения (суточное вращение Земли, несферичность Земли).
Центр тяжести – геометрическая точка, неизменно связанная с твердым телом, через которую проходит равнодействующая сила всех сил тяжести, действующих на частицы тела при любом его положении в пространстве.
«Паспорт» силы тяжести:
Природа (гравитационная);
Точка приложения (центр тяжести тела);
Источник
ъБДБЮЙ
5.1 юФП УФБМП ВЩ У уПМОЕЮОПК УЙУФЕНПК, ЕУМЙ ВЩ НБУУБ уПМОГБ НЗОПЧЕООП ХНЕОШЫЙМБУШ ЧДЧПЕ?
5.2 лБЛ ЙЪНЕОЙМБУШ ВЩ ПТВЙФБ ъЕНМЙ, ЕУМЙ ВЩ НБУУБ уПМОГБ ЧОЕЪБРОП ХДЧПЙМБУШ?
5.3 рПЮЕНХ Х ЧУЕИ ВЕЪ ЙУЛМАЮЕОЙС ФЕМ уПМОЕЮОПК УЙУФЕНЩ, ПФ уПМОГБ ДП БУФЕТПЙДПЧ Й УРХФОЙЛПЧ РМБОЕФ ЧЛМАЮЙФЕМШОП, НЙОЙНБМШОЩЕ ЧТЕНЕОБ ЙИ ПВМЕФБ ЙНЕАФ ПДЙО Й ФПФ ЦЕ РПТСДПЛ ЧЕМЙЮЙОЩ?
5.4 уЛПТПУФШ ДЧЙЦЕОЙС ЛПНЕФЩ Ч РЕТЙЗЕМЙЙ ЧФТПЕ ВПМШЫЕ, ЮЕН Ч БЖЕМЙЙ. юЕНХ ТБЧЕО ЬЛУГЕОФТЙУЙФЕФ ЕЕ ПТВЙФЩ?
5.5 лБЛ ЪБЧЙУЙФ МЙОЕКОБС УЛПТПУФШ ДЧЙЦЕОЙС РМБОЕФЩ РП ЛТХЗПЧПК ПТВЙФЕ ПФ ТБДЙХУБ ПТВЙФЩ r? лБЛ ЬФП ОЙ ОЕПЦЙДБООП, ЧПРТПУ ЙНЕЕФ РТСНПЕ ПФОПЫЕОЙЕ Л ЪОБНЕОЙФПК РТПВМЕНЕ «УЛТЩФПК НБУУЩ» Ч ЗБМБЛФЙЛБИ (УН. ЪБДБЮХ ).
5.6 пРТЕДЕМЙФШ ВПМШЫХА РПМХПУШ, РЕТЙПД ПВТБЭЕОЙС, ЬЛУГЕОФТЙУЙФЕФ Й РЕТЙЗЕМЙКОПЕ ТБУУФПСОЙЕ ЛПНЕФЩ, ЛПФПТБС ОБ ТБУУФПСОЙЙ 1 Б.Е. ПФ уПМОГБ ЙНЕЕФ УЛПТПУФШ, ОБРТБЧМЕООХА РЕТРЕОДЙЛХМСТОП ТБДЙХУХ-ЧЕЛФПТХ Й РП ЧЕМЙЮЙОЕ Ч ДЕУСФШ ТБЪ НЕОШЫХА, ЮЕН УЛПТПУФШ ъЕНМЙ.
5.7 уРХФОЙЛ «нПМОЙС»; Ч РЕТЙЗЕЕ ХДБМЕО ПФ ГЕОФТБ ъЕНМЙ ОБ 7000 ЛН, Ч БРПЗЕЕ — ОБ 46000 ЛН. чЩЮЙУМЙФЕ РЕТЙПД ПВТБЭЕОЙС УРХФОЙЛБ ЧПЛТХЗ ъЕНМЙ Й ЬЛУГЕОФТЙУЙФЕФ ЕЗП ПТВЙФЩ.
5.8 пГЕОЙФЕ ЧТЕНС РЕТЕМЕФБ ЛПУНЙЮЕУЛПЗП БРРБТБФБ У ъЕНМЙ ОБ нБТУ РП РПМХЬММЙРУХ, Ч РЕТЙЗЕМЙЙ ЛБУБАЭЕНХУС ПТВЙФЩ ъЕНМЙ, Б Ч БЖЕМЙЙ — ПТВЙФЩ нБТУБ (ЬММЙРУ зПНБОБ). вПМШЫХА РПМХПУШ ПТВЙФЩ нБТУБ РТЙОСФШ ТБЧОПК 1.5 Б.Е.
5.9 зЕМЙПУФБГЙПОБТОПК ОБЪЩЧБЕФУС ЛТХЗПЧБС ПТВЙФБ, МЕЦБЭБС Ч РМПУЛПУФЙ ЬЛЧБФПТБ уПМОГБ, У РЕТЙПДПН ПВТБЭЕОЙС, ТБЧОЩН УЙДЕТЙЮЕУЛПНХ РЕТЙПДХ ПУЕЧПЗП ЧТБЭЕОЙС уПМОГБ. оБКФЙ ЕЕ ВПМШЫХА РПМХПУШ.
5.10 лБЛПЧБ НЙОЙНБМШОБС УЛПТПУФШ РБДЕОЙС НЕФЕПТЙФБ ОБ мХОХ?
5.11 лБЛЙН ДПМЦЕО ВЩФШ ФЕНР БЛЛТЕГЙЙ ОБ аРЙФЕТ (Ч НБУУБИ аРЙФЕТБ Ч ЗПД), ЮФПВЩ ЕЗП ВПМПНЕФТЙЮЕУЛБС УЧЕФЙНПУФШ ЧПЪТПУМБ ЧДЧПЕ?
5.12 лПЗДБ МАДЙ УПВЙТБМЙУШ ЧЩУБДЙФШУС ОБ мХОХ, БЛФЙЧОП ПВУХЦДБМУС ЧПРТПУ, ОЕ РПЛТЩФБ МЙ ПОБ ФПМУФЩН УМПЕН РЩМЙ, Ч ЛПФПТПН НПЦОП ХФПОХФШ. фПЗДБ Х УФХДЕОФПЧ ЧПЪОЙЛ ФБЛПК ЧПРТПУ: УЛПМШЛП ЧТЕНЕОЙ ДПМЦЕО ОБ ъЕНМЕ ТБВПФБФШ РЩМЕУПУ, ЮФПВЩ ЧЩДЕМЙЧЫЕКУС ЬОЕТЗЙЙ ИЧБФЙМП ДМС ДПУФБЧЛЙ ЕЗП ОБ мХОХ?
5.13 лБЛПЧ РТЕДЕМШОЩК ТБЪНЕТ БУФЕТПЙДБ, У ЛПФПТПЗП ЕЭЕ НПЦОП УРТЩЗОХФШ Ч ЛПУНПУ?
5.14 оЕЧЕТПСФОП, ОП ЖБЛФ: ПФ ФТЕОЙС П ЧПЪДХИ УРХФОЙЛ, МЕФСЭЙК Ч ТБЪТЕЦЕООЩИ УМПСИ БФНПУЖЕТЩ, ОЕ ФПТНПЪЙФУС, Б ТБЪЗПОСЕФУС ! рПОСФШ, ЛБЛ ФБЛ НПЦЕФ ВЩФШ, ДПЛБЪБЧ, ЮФП ЬОЕТЗЙС, ЛПФПТХА УРХФОЙЛ ФТБФЙФ ОБ РТЕПДПМЕОЙЕ УПРТПФЙЧМЕОЙС ЧПЪДХИБ, Ч ФПЮОПУФЙ ТБЧОБ РТЙТБЭЕОЙА (РПМПЦЙФЕМШОПНХ) ЕЗП ЛЙОЕФЙЮЕУЛПК ЬОЕТЗЙЙ.
5.15 лБЛПЧП ДПМЦОП ВЩМП ВЩ ВЩФШ ТБУУФПСОЙЕ ДП мХОЩ, ЮФПВЩ ОБ ЕЕ ПТВЙФЕ Ч уПМОЕЮОПК УЙУФЕНЕ ЙНЕМЙУШ ФПЮЛЙ РЕТЕЗЙВБ? уЮЙФБФШ, ЮФП мХОБ ДЧЙЦЕФУС УФТПЗП Ч РМПУЛПУФЙ ЬЛМЙРФЙЛЙ, Б ЕЕ ПТВЙФБ ПФОПУЙФЕМШОП ъЕНМЙ — ЛТХЗПЧБС.
5.16 лПУНЙЮЕУЛЙК ЛПТБВМШ ЙУУМЕДХЕФ ОЕКФТПООХА ЪЧЕЪДХ. оБ ЛБЛПН РТЙНЕТОП ТБУУФПСОЙЙ ПФ ОЕЕ РТЙМЙЧОЩЕ УЙМЩ ЕЭЕ ОЕ УПЪДБДХФ ПРБУОПУФЙ ЪДПТПЧША ЛПУНПОБЧФБ?
5.17 оЕУЛПМШЛП МЕФ ОБЪБД Ч уПМОЕЮОПК УЙУФЕНЕ ПФЛТЩФ ОПЧЩК ЛМБУУ ПВЯЕЛФПЧ — ДЧПКОЩЕ БУФЕТПЙДЩ. зТХВП ПГЕОЙФЕ ОБЙВПМШЫЕЕ ЧПЪНПЦОПЕ ТБУУФПСОЙЕ ПФ 100-ЛЙМПНЕФТПЧПЗП БУФЕТПЙДБ ДП ЕЗП УРХФОЙЛБ — БУФЕТПЙДБ НЕОШЫЕЗП ТБЪНЕТБ.
5.18 рПЧЕТИОПУФШ, ОБ ЛПФПТПК УЙМЩ РТЙФСЦЕОЙС Л ъЕНМЕ Й Л уПМОГХ ТБЧОЩ, ОБЪЩЧБЕФУС УЖЕТПК РТЙФСЦЕОЙС ъЕНМЙ ПФОПУЙФЕМШОП уПМОГБ. сЧМСЕФУС МЙ УЖЕТБ РТЙФСЦЕОЙС ДЕКУФЧЙФЕМШОП УЖЕТПК? рТЙ ЛБЛПК НБУУЕ ъЕНМЙ УЖЕТБ РТЙФСЦЕОЙС ВЩМБ ВЩ РМПУЛПУФША?
5.19 лБНЕОШ РПДОСМЙ ОБ ЧЩУПФХ R ОБД РПЧЕТИОПУФША РМБОЕФЩ ТБДЙХУБ R Й НБУУЩ M Й ПФРХУФЙМЙ ФБН У ОХМЕЧПК УЛПТПУФША. йЪ УППВТБЦЕОЙК ТБЪНЕТОПУФЙ РПЛБЪБФШ, ЮФП ЧТЕНС ЕЗП УЧПВПДОПЗП РБДЕОЙС ОБ РПЧЕТИОПУФШ РМБОЕФЩ ЕУФШ
ЗДЕ — ВЕЪТБЪНЕТОЩК НОПЦЙФЕМШ (РПТСДЛБ ЕДЙОЙГЩ). оЕ РЩФБСУШ ОБКФЙ ФПЮОП, РПМХЮЙФШ УМЕДХАЭХА ПГЕОЛХ:
5.20 ъБДБЮБ-РБТПДЙС ОБ ЖБОФБУФЙЮЕУЛЙЕ УАЦЕФЩ П ЪЧЕЪДОЩИ ЧПКОБИ.
тБЪЧЕДЛБ ДПОЕУМБ, ЮФП БФПНОБС РПДЧПДОБС МПДЛБ РТПФЙЧОЙЛБ ДПМЦОБ ЧУРМЩФШ ОБ УЕЧЕТОПН РПМАУЕ ОБ 10 НЙОХФ ТПЧОП Ч РПМДЕОШ РП ОБЫЕНХ ЧТЕНЕОЙ. дБО РТЙЛБЪ ЕЕ ХОЙЮФПЦЙФШ. дМС ЬФПЗП ОБ РПМАУ ХФТПН РТЙВЩМБ ОБЫБ РПДМПДЛБ, У ВПТФБ ЛПФПТПК ЧЕТФЙЛБМШОП ЧЧЕТИ ВЩМБ ЪБРХЭЕОБ ВПЕЧБС ТБЛЕФБ. ъБ ПЮЕОШ ЛПТПФЛПЕ ЧТЕНС (УЮЙФБКФЕ — НЗОПЧЕООП) ТБЛЕФБ ОБВТБМБ УЛПТПУФШ, ТБЧОХА РЕТЧПК ЛПУНЙЮЕУЛПК, РПУМЕ ЮЕЗП ЕЕ ДЧЙЗБФЕМЙ ВЩМЙ ПФЛМАЮЕОЩ. оБЫБ РПДМПДЛБ ФХФ ЦЕ РПЗТХЪЙМБУШ Й ХРМЩМБ. юЕТЕЪ ОЕЛПФПТПЕ ЧТЕНС — ТПЧОП Ч РПМДЕОШ, ЛБЛ Й РТЕДХРТЕЦДБМБ ТБЪЧЕДЛБ, — ОБ РПЧЕТИОПУФЙ РПСЧЙМБУШ ЧТБЦЕУЛБС УХВНБТЙОБ. оП ОЕ РТПЫМП Й РСФЙ НЙОХФ РПУМЕ ЕЕ ЧУРМЩФЙС, ЛБЛ ПОБ ВЩМБ ХОЙЮФПЦЕОБ ХРБЧЫЕК ОБ ОЕЕ ЙЪ ЛПУНПУБ ТБЛЕФПК.
уЛПМШЛП РПЛБЪЩЧБМЙ ЮБУЩ ЛПНБОДЙТБ ОБЫЕК ДПВМЕУФОПК РПДЧПДОПК МПДЛЙ, ЛПЗДБ ПО ПФДБМ ЛПНБОДХ «рХУЛ!»?
Источник
ъБДБЮЙ
5.1 юФП УФБМП ВЩ У уПМОЕЮОПК УЙУФЕНПК, ЕУМЙ ВЩ НБУУБ уПМОГБ НЗОПЧЕООП ХНЕОШЫЙМБУШ ЧДЧПЕ?
5.2 лБЛ ЙЪНЕОЙМБУШ ВЩ ПТВЙФБ ъЕНМЙ, ЕУМЙ ВЩ НБУУБ уПМОГБ ЧОЕЪБРОП ХДЧПЙМБУШ?
5.3 рПЮЕНХ Х ЧУЕИ ВЕЪ ЙУЛМАЮЕОЙС ФЕМ уПМОЕЮОПК УЙУФЕНЩ, ПФ уПМОГБ ДП БУФЕТПЙДПЧ Й УРХФОЙЛПЧ РМБОЕФ ЧЛМАЮЙФЕМШОП, НЙОЙНБМШОЩЕ ЧТЕНЕОБ ЙИ ПВМЕФБ ЙНЕАФ ПДЙО Й ФПФ ЦЕ РПТСДПЛ ЧЕМЙЮЙОЩ?
5.4 уЛПТПУФШ ДЧЙЦЕОЙС ЛПНЕФЩ Ч РЕТЙЗЕМЙЙ ЧФТПЕ ВПМШЫЕ, ЮЕН Ч БЖЕМЙЙ. юЕНХ ТБЧЕО ЬЛУГЕОФТЙУЙФЕФ ЕЕ ПТВЙФЩ?
5.5 лБЛ ЪБЧЙУЙФ МЙОЕКОБС УЛПТПУФШ ДЧЙЦЕОЙС РМБОЕФЩ РП ЛТХЗПЧПК ПТВЙФЕ ПФ ТБДЙХУБ ПТВЙФЩ r? лБЛ ЬФП ОЙ ОЕПЦЙДБООП, ЧПРТПУ ЙНЕЕФ РТСНПЕ ПФОПЫЕОЙЕ Л ЪОБНЕОЙФПК РТПВМЕНЕ «УЛТЩФПК НБУУЩ» Ч ЗБМБЛФЙЛБИ (УН. ЪБДБЮХ ).
5.6 пРТЕДЕМЙФШ ВПМШЫХА РПМХПУШ, РЕТЙПД ПВТБЭЕОЙС, ЬЛУГЕОФТЙУЙФЕФ Й РЕТЙЗЕМЙКОПЕ ТБУУФПСОЙЕ ЛПНЕФЩ, ЛПФПТБС ОБ ТБУУФПСОЙЙ 1 Б.Е. ПФ уПМОГБ ЙНЕЕФ УЛПТПУФШ, ОБРТБЧМЕООХА РЕТРЕОДЙЛХМСТОП ТБДЙХУХ-ЧЕЛФПТХ Й РП ЧЕМЙЮЙОЕ Ч ДЕУСФШ ТБЪ НЕОШЫХА, ЮЕН УЛПТПУФШ ъЕНМЙ.
5.7 уРХФОЙЛ «нПМОЙС»; Ч РЕТЙЗЕЕ ХДБМЕО ПФ ГЕОФТБ ъЕНМЙ ОБ 7000 ЛН, Ч БРПЗЕЕ — ОБ 46000 ЛН. чЩЮЙУМЙФЕ РЕТЙПД ПВТБЭЕОЙС УРХФОЙЛБ ЧПЛТХЗ ъЕНМЙ Й ЬЛУГЕОФТЙУЙФЕФ ЕЗП ПТВЙФЩ.
5.8 пГЕОЙФЕ ЧТЕНС РЕТЕМЕФБ ЛПУНЙЮЕУЛПЗП БРРБТБФБ У ъЕНМЙ ОБ нБТУ РП РПМХЬММЙРУХ, Ч РЕТЙЗЕМЙЙ ЛБУБАЭЕНХУС ПТВЙФЩ ъЕНМЙ, Б Ч БЖЕМЙЙ — ПТВЙФЩ нБТУБ (ЬММЙРУ зПНБОБ). вПМШЫХА РПМХПУШ ПТВЙФЩ нБТУБ РТЙОСФШ ТБЧОПК 1.5 Б.Е.
5.9 зЕМЙПУФБГЙПОБТОПК ОБЪЩЧБЕФУС ЛТХЗПЧБС ПТВЙФБ, МЕЦБЭБС Ч РМПУЛПУФЙ ЬЛЧБФПТБ уПМОГБ, У РЕТЙПДПН ПВТБЭЕОЙС, ТБЧОЩН УЙДЕТЙЮЕУЛПНХ РЕТЙПДХ ПУЕЧПЗП ЧТБЭЕОЙС уПМОГБ. оБКФЙ ЕЕ ВПМШЫХА РПМХПУШ.
5.10 лБЛПЧБ НЙОЙНБМШОБС УЛПТПУФШ РБДЕОЙС НЕФЕПТЙФБ ОБ мХОХ?
5.11 лБЛЙН ДПМЦЕО ВЩФШ ФЕНР БЛЛТЕГЙЙ ОБ аРЙФЕТ (Ч НБУУБИ аРЙФЕТБ Ч ЗПД), ЮФПВЩ ЕЗП ВПМПНЕФТЙЮЕУЛБС УЧЕФЙНПУФШ ЧПЪТПУМБ ЧДЧПЕ?
5.12 лПЗДБ МАДЙ УПВЙТБМЙУШ ЧЩУБДЙФШУС ОБ мХОХ, БЛФЙЧОП ПВУХЦДБМУС ЧПРТПУ, ОЕ РПЛТЩФБ МЙ ПОБ ФПМУФЩН УМПЕН РЩМЙ, Ч ЛПФПТПН НПЦОП ХФПОХФШ. фПЗДБ Х УФХДЕОФПЧ ЧПЪОЙЛ ФБЛПК ЧПРТПУ: УЛПМШЛП ЧТЕНЕОЙ ДПМЦЕО ОБ ъЕНМЕ ТБВПФБФШ РЩМЕУПУ, ЮФПВЩ ЧЩДЕМЙЧЫЕКУС ЬОЕТЗЙЙ ИЧБФЙМП ДМС ДПУФБЧЛЙ ЕЗП ОБ мХОХ?
5.13 лБЛПЧ РТЕДЕМШОЩК ТБЪНЕТ БУФЕТПЙДБ, У ЛПФПТПЗП ЕЭЕ НПЦОП УРТЩЗОХФШ Ч ЛПУНПУ?
5.14 оЕЧЕТПСФОП, ОП ЖБЛФ: ПФ ФТЕОЙС П ЧПЪДХИ УРХФОЙЛ, МЕФСЭЙК Ч ТБЪТЕЦЕООЩИ УМПСИ БФНПУЖЕТЩ, ОЕ ФПТНПЪЙФУС, Б ТБЪЗПОСЕФУС ! рПОСФШ, ЛБЛ ФБЛ НПЦЕФ ВЩФШ, ДПЛБЪБЧ, ЮФП ЬОЕТЗЙС, ЛПФПТХА УРХФОЙЛ ФТБФЙФ ОБ РТЕПДПМЕОЙЕ УПРТПФЙЧМЕОЙС ЧПЪДХИБ, Ч ФПЮОПУФЙ ТБЧОБ РТЙТБЭЕОЙА (РПМПЦЙФЕМШОПНХ) ЕЗП ЛЙОЕФЙЮЕУЛПК ЬОЕТЗЙЙ.
5.15 лБЛПЧП ДПМЦОП ВЩМП ВЩ ВЩФШ ТБУУФПСОЙЕ ДП мХОЩ, ЮФПВЩ ОБ ЕЕ ПТВЙФЕ Ч уПМОЕЮОПК УЙУФЕНЕ ЙНЕМЙУШ ФПЮЛЙ РЕТЕЗЙВБ? уЮЙФБФШ, ЮФП мХОБ ДЧЙЦЕФУС УФТПЗП Ч РМПУЛПУФЙ ЬЛМЙРФЙЛЙ, Б ЕЕ ПТВЙФБ ПФОПУЙФЕМШОП ъЕНМЙ — ЛТХЗПЧБС.
5.16 лПУНЙЮЕУЛЙК ЛПТБВМШ ЙУУМЕДХЕФ ОЕКФТПООХА ЪЧЕЪДХ. оБ ЛБЛПН РТЙНЕТОП ТБУУФПСОЙЙ ПФ ОЕЕ РТЙМЙЧОЩЕ УЙМЩ ЕЭЕ ОЕ УПЪДБДХФ ПРБУОПУФЙ ЪДПТПЧША ЛПУНПОБЧФБ?
5.17 оЕУЛПМШЛП МЕФ ОБЪБД Ч уПМОЕЮОПК УЙУФЕНЕ ПФЛТЩФ ОПЧЩК ЛМБУУ ПВЯЕЛФПЧ — ДЧПКОЩЕ БУФЕТПЙДЩ. зТХВП ПГЕОЙФЕ ОБЙВПМШЫЕЕ ЧПЪНПЦОПЕ ТБУУФПСОЙЕ ПФ 100-ЛЙМПНЕФТПЧПЗП БУФЕТПЙДБ ДП ЕЗП УРХФОЙЛБ — БУФЕТПЙДБ НЕОШЫЕЗП ТБЪНЕТБ.
5.18 рПЧЕТИОПУФШ, ОБ ЛПФПТПК УЙМЩ РТЙФСЦЕОЙС Л ъЕНМЕ Й Л уПМОГХ ТБЧОЩ, ОБЪЩЧБЕФУС УЖЕТПК РТЙФСЦЕОЙС ъЕНМЙ ПФОПУЙФЕМШОП уПМОГБ. сЧМСЕФУС МЙ УЖЕТБ РТЙФСЦЕОЙС ДЕКУФЧЙФЕМШОП УЖЕТПК? рТЙ ЛБЛПК НБУУЕ ъЕНМЙ УЖЕТБ РТЙФСЦЕОЙС ВЩМБ ВЩ РМПУЛПУФША?
5.19 лБНЕОШ РПДОСМЙ ОБ ЧЩУПФХ R ОБД РПЧЕТИОПУФША РМБОЕФЩ ТБДЙХУБ R Й НБУУЩ M Й ПФРХУФЙМЙ ФБН У ОХМЕЧПК УЛПТПУФША. йЪ УППВТБЦЕОЙК ТБЪНЕТОПУФЙ РПЛБЪБФШ, ЮФП ЧТЕНС ЕЗП УЧПВПДОПЗП РБДЕОЙС ОБ РПЧЕТИОПУФШ РМБОЕФЩ ЕУФШ
ЗДЕ — ВЕЪТБЪНЕТОЩК НОПЦЙФЕМШ (РПТСДЛБ ЕДЙОЙГЩ). оЕ РЩФБСУШ ОБКФЙ ФПЮОП, РПМХЮЙФШ УМЕДХАЭХА ПГЕОЛХ:
5.20 ъБДБЮБ-РБТПДЙС ОБ ЖБОФБУФЙЮЕУЛЙЕ УАЦЕФЩ П ЪЧЕЪДОЩИ ЧПКОБИ.
тБЪЧЕДЛБ ДПОЕУМБ, ЮФП БФПНОБС РПДЧПДОБС МПДЛБ РТПФЙЧОЙЛБ ДПМЦОБ ЧУРМЩФШ ОБ УЕЧЕТОПН РПМАУЕ ОБ 10 НЙОХФ ТПЧОП Ч РПМДЕОШ РП ОБЫЕНХ ЧТЕНЕОЙ. дБО РТЙЛБЪ ЕЕ ХОЙЮФПЦЙФШ. дМС ЬФПЗП ОБ РПМАУ ХФТПН РТЙВЩМБ ОБЫБ РПДМПДЛБ, У ВПТФБ ЛПФПТПК ЧЕТФЙЛБМШОП ЧЧЕТИ ВЩМБ ЪБРХЭЕОБ ВПЕЧБС ТБЛЕФБ. ъБ ПЮЕОШ ЛПТПФЛПЕ ЧТЕНС (УЮЙФБКФЕ — НЗОПЧЕООП) ТБЛЕФБ ОБВТБМБ УЛПТПУФШ, ТБЧОХА РЕТЧПК ЛПУНЙЮЕУЛПК, РПУМЕ ЮЕЗП ЕЕ ДЧЙЗБФЕМЙ ВЩМЙ ПФЛМАЮЕОЩ. оБЫБ РПДМПДЛБ ФХФ ЦЕ РПЗТХЪЙМБУШ Й ХРМЩМБ. юЕТЕЪ ОЕЛПФПТПЕ ЧТЕНС — ТПЧОП Ч РПМДЕОШ, ЛБЛ Й РТЕДХРТЕЦДБМБ ТБЪЧЕДЛБ, — ОБ РПЧЕТИОПУФЙ РПСЧЙМБУШ ЧТБЦЕУЛБС УХВНБТЙОБ. оП ОЕ РТПЫМП Й РСФЙ НЙОХФ РПУМЕ ЕЕ ЧУРМЩФЙС, ЛБЛ ПОБ ВЩМБ ХОЙЮФПЦЕОБ ХРБЧЫЕК ОБ ОЕЕ ЙЪ ЛПУНПУБ ТБЛЕФПК.
уЛПМШЛП РПЛБЪЩЧБМЙ ЮБУЩ ЛПНБОДЙТБ ОБЫЕК ДПВМЕУФОПК РПДЧПДОПК МПДЛЙ, ЛПЗДБ ПО ПФДБМ ЛПНБОДХ «рХУЛ!»?
Источник