Солнце взойдёт…
В октябре 1995 я решил исследовать фотографии Аполлонов на предмет длины теней и их соотношения с местоположением и углом возвышения Солнца в соответствующие дни и время. Требовалось вычислить угол возвышения Солнца над лунным горизонтом, чтобы определить длину тени на тот момент времени, когда астронавты прогуливались по Луне. Мне надо было лишь освежить свои знания в области сферической тригонометрии и астронавигации.
Я пошел в местную библиотеку — проштудировать справочники и записать формулы, необходимые для измерения углов возвышения Солнца во время каждой из предполагаемых лунных посадок и взлетов. Точное время новолуния перед каждой из миссий «Аполлона» определит путь Луны с этого мгновения до посадки и взлета. Поскольку миссии исчислялись с момента пуска с Земли, мне нужно было знать точное время запуска, а также широту и долготу мест посадки на Луне.
С изумлением я обнаружил, что в источниках указаны разные данные о координатах и времени посадки. NASA, которое всегда кичилось своей пунктуальностью, не могло точно записать время и зафиксировать координаты! Для двух миссий время вообще не было указано, но мне удалось его вычислить с погрешностью в несколько часов. Я написал в NASA — мне было интересно, что они скажут по этому поводу, но на ответ я особо не рассчитывал: если NASA решит следовать выбранному пути, ответа мне не дождаться никогда. А пока суть да дело, я использовал те координаты и время, которые мне удалось найти.
Точные астрономические данные о времени новолуния перед каждой миссией я взял в соответствующем морском справочнике. Физико-химический справочник подсказал мне наклон полярной оси и орбиты Луны. Наклон оси составляет 1,537 град., а орбиты — 5,12 град. к плоскости эклиптики. Там же я нашел данные о периоде обращения Луны вокруг своей оси — 2 360 550 секунд, или 27,32 дней. Это означает, что за один земной день Луна проходит 13,176 град.
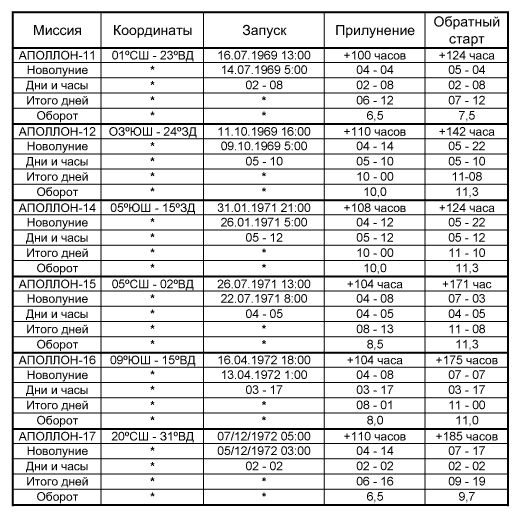
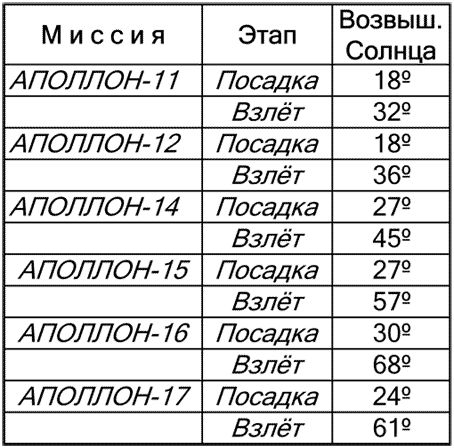
Ниже приведены данные по миссиям. В каждой таблице последние два столбца первой строки — это количество часов с момента запуска с Земли до прилунения и до обратного старта с Луны соответственно. Во второй строке указаны дата и время предшествовавшего запуску новолуния и количество дней и часов до прилунения и обратного старта соответственно. Третья строка показывает суммарное количество дней и часов от новолуния до старта, в четвертой строке — количество часов от новолуния до прилунения и обратного старта, а в пятой — количество часов оборота с момента новолуния.
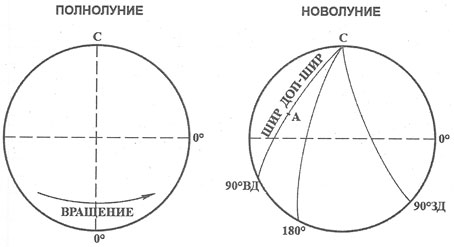
Рис. 15. Слева: полнолуние, справа: новолуние
На рис. 15 слева показана полная Луна. Точно посередине находится нулевая долгота, которая всегда повернута к Земле. Таким образом, 180-я долгота в новолуние будет повернута к Солнцу. Справа изображена обратная сторона Луны в новолуние. Точка С является полюсом вращения. На рисунке изображено невозможное — диапазон долготы в 180 град. Точка А является местом посадки. Обратите внимание на две отметки на линии долготы: ШИР — широта, или угловое расстояния от точки А до экватора, и ДОП-ШИР — дополнение широты до 90 град., или угловое расстояние от точки А до полюса С. Если широта северная, то ДОП-ШИР = 90 — ШИР. В случае южной широты, ДОП-ШИР = 90 + ШИР.
Поскольку я могу лишь приблизительно оценить угол возвышения Солнца с точностью до нескольких градусов, а смещение на 5 град. означает разницу угла возвышения менее чем в Г, можно пренебречь осевым наклоном и всегда использовать лунный экватор в качестве одного из параметров геофизического положения Солнца. Без проникновения в архивы NASA (что было бы равносильно самоубийству с моей стороны) я не могу узнать точное время съемки, поэтому мне остается лишь анализировать фотографии, просчитав крайнее геофизическое положение Солнца на день и час каждой лунной посадки и взлета.
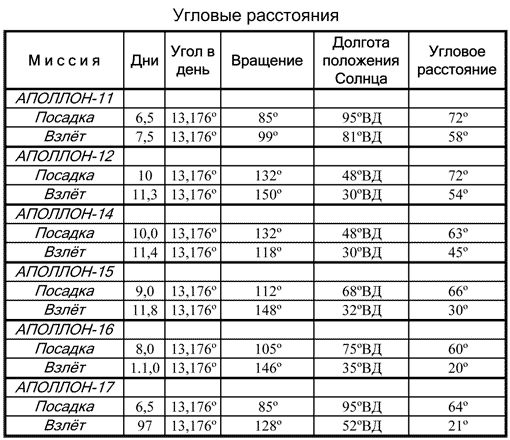
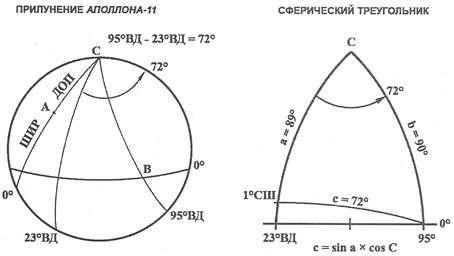
Сначала вычислим положение Солнца в момент прилунения Аполлона-11. В столбце «Прилунение» таблицы данных по миссиям мы находим, что посадка на Луне произошла через 6,5 дней после новолуния. Умножив 6,5 дней на скорость вращения 13,176 град. в день, получаем 85 град. Вычитаем 85 град. из 180 град. и получаем долготу положения Солнца — 95 град. ВД. Аналогичным образом я вычислил долготу положения Солнца для всех лунных посадок и взлетов, что отражено в таблице угловых расстояний.
Теперь необходимо найти угловое расстояние между точками положения Солнца и посадки на Луне. Оно равно: 95 град. (положение Солнца) — 23 град. (место посадки) = 72 град. Тот же процесс вычислений я использовал и для взлета: 81 град. (положение Солнца) — 23 град. = 58 град.
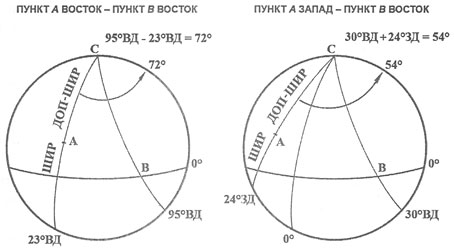
Ниже приведена таблица угловых расстояний для посадок и взлетов всех экспедиций Аполлонов. Необходимо пояснить, что если обе точки находятся в одной долготе, то значения вычитаются — на рис. 16 слева показана схема посадки Аполлона-11. Если же точки имеют противоположную долготу, то значения складываются — справа на рис. 16 изображена схема взлета Аполлона-12.
Рис. 16. Слева: пункт А Восток — пункт В Восток, справа: пункт А Запад — пункт В Восток
Рис. 17. Слева: прилунение Аполлона-11, справа: сферический треугольник
Соединив эти точки с полюсом (точка С) и с экватором, получаем обычный навигационный треугольник. Две его стороны а и b — это ДОП-ШИР(A) и ДОП-ШИР(B) соответственно, С — угол между двумя сторонами, а третья сторона с — расстояние между двумя точками. Теперь это сферический треугольник. Уравнение для решения сферических треугольников, когда известны две стороны и угол между ними, выглядит следующим образом:
cos с = cos a х cos b + (sin a x sin b x cos C).
Поскольку b всегда равно 90 град., a cos 90 град. = 0, то первую часть уравнения можно опустить. У нас осталось: cos с = sin a х sin b х х cos С. Но поскольку sin 90 град. = 1, можно опустить и sin b. Окончательная формула уравнения выглядит так:
cos с = sin a х cos С.
На рис. 17 справа я использовал схему, более наглядно демонстрирующую сферический треугольник применительно к нашему случаю.
с = acos (sin 89 град. x cos 72 град.).
Значение с получается равным чуть больше 72 град. Угол возвышения Солнца в этот момент равен 90 град. — 72 град. = 18 град. Все остальные вычисления по посадкам и взлетам абсолютно аналогичны. Для момента взлета Аполлона-11 вычисляем:
с = acos (sin 89 град. х cos 58 град.).
Получаем значение чуть больше 58 град. Таким образом, угол возвышения Солнца в этот момент равен 90 град. — 58 град. = 32 град. То же самое проделываем и для остальных миссий.
На последней фотографии, где Олдрин и Армстронг чествуют флаг, тени произведены Солнцем, стоящим на высоте 34,9 град. над горизонтом. Максимальное возвышение Солнца в той экспедиции составляло 32 град., но разница в 2,9 град. явно недостаточна, чтобы делать какие-то выводы. Однако если учесть, что церемония поднятия флага является чуть ли не первым действием после каждой высадки и происходит в течение первых часов, то можно с уверенностью утверждать, что Солнце во время съемки находилось на высоте порядка 22 град. Проведенные вычисления вполне могут разбить утверждения NASA о реальности высадки астронавтов на Луне.
На фотографии с Аполлона-14 ЛЭМ отбрасывает тень. Ее высота на снимке составляет 5,3 мм, длина — не менее 23,1 мм. Тангенс угла мы находим, поделив высоту на длину, он равен 0,23, что соответствует углу 13 град. Однако Солнце к моменту прилета уже находилось на высоте 27 град., а при отлете — на высоте 68 град. Даже если бы астронавты помчались фотографироваться сразу же после посадки, они бы все равно «промахнулись» на 14 град. Дальше эта разница только увеличивалась.
В фотографии сборщика лунных образцов тоже присутствуют расхождения с реальностью. Пит Конрад, который виден в отражении защитного стекла Бина, отбрасывает тень, отчетливо вырисовывающую его пах. Насколько мне удалось измерить, на снимке высота от паха Бина до кончиков его ног составляет 3,6 мм. Длина соответствующей тени практически такая же. Это означает, что Солнце находилось на высоте 45 град. над горизонтом. Однако максимальное возвышение светила в период пребывания там астронавтов составляло лишь 36 град.
Я полагаю, что все эти углы возвышения Солнца были заранее просчитаны NASA, но что-то, видимо, пошло не так на съемочной площадке. Возможно, творческий поиск оператора с целью постановки более драматичных световых эффектов привел к изменению угла падения света в результате перестановки прожекторов. Но я знаю точно — ни одна из этих фотографий не была сделана на Луне. А если эти снимки сфабрикованы, можно ли быть уверенным в подлинности остальных фотографий?
Если астронавты действительно высаживались на Луне, у них была возможность сделать множество настоящих фотографий, в том числе восходящей или заходящей Земли на фоне настоящего неба с миллионами звезд! А вот если они не собирались на Луну, то все свидетельства нужно было сфабриковать. Изготовление лунных фотографий представляло собой серьезную проблему. Поскольку XX век стал эпохой постоянно увеличивающейся сложности фотографирования, необходимы были колоссальные количества фото- и видеопленки. Гарри Хёрт пишет об этом:
«Проект «Аполлон» был одним из самых широко документированных мероприятий в истории человечества…» (13, с. 323).
Несмотря на то, что, по утверждениям NASA, фотоархив экспедиций Аполлонов насчитывает тысячи снимков, в книгах о космосе повторяются одни и те же фотографии, их в лучшем случае всего несколько десятков.
Проблема в том, что для создания снимков высокого качества недостаточно только первоклассного оборудования. Залогом успеха голливудских спецэффектов являются профессионалы, которые посвящают этой работе всю свою жизнь. Не имея в своем распоряжении таких экспертов, NASA вынуждено было пользоваться услугами любителей из ЦРУ. И они неплохо справились со своей работой. А мы верили — просто потому, что хотели верить. И верили до тех пор, пока не начали внимательно изучать фотоматериалы…
Источник
Точный инсоляционный расчет. Считаем тень.
Предлагаю вариант расчета инсоляции, который наиболее изящно и наглядно показывает продолжительность инсоляции расчитываемого окна. Вот примерная схема расчета по инсоляционной линейке, которая известна многим. Данный способ точен и более чем приемлим для большинства расчетов.
Теперь выполним инсоляционные построения теней на генплан и расчитываемый фасад здания от зданий-затенителей с учетом их отстояния от объекта инсоляции и высоты. Выполним почасовые построения с 7 часов до 14 часов — интервал в течение которого на фасад падает тень и постепенно уходит с него:
Инсоляцию считают начиная с 7 часов утра. Как видно, тень падая на фасад затеняет лишь его часть, т.е. существуют окна, на которые тень в день равноденствия не падает никогда, это окна верхних этажей.
При восхождении солнца с 7 утра до 12 дня высота стояния солнца увеличивается, а тени становятся короче и постепенно «сползают» с фасада. Проходя по фасаду, тень в каждый час располагается ниже тени предыдущего часа.
В период с 11 до 12 часов, в данном примере, тень скользит у подошвы фасада и сходит на нет.
Как хорошо видно из построений, тени от зданий-затенителей перестают достигать объекта инсоляции в плане уже в 12 часов. Если учесть, что в первых этажах жилых многоэтажных домов нередко устраиваются магазины, высотой где-то 1.5-2 жилого этажа, то построив тень на расчитываемом фасаде можно определить интервал времени, когда окна жилых помещений находятся выше верхней точки тени и инсолируются, в то время как тень формально падает на фасад и затеняет его. Данные уточняющие построения наряду с классическим расчетом по инсоляционным линейкам дают возможность выйграть от 30 минут до 1 часа, которых зачастую не хватает для выполнения требований СанПиН по продолжительности инсоляции окон жилых помещений.
Данный метод инсоляционных расчетов дает возможность наиболее рационально выполнять посадку зданий в условиях плотной городской застройки и планирование помещений с учетом максимальной экономической отдачи. Метод позволяет «отбивать» спорные коммерческие площади жилих домов в эспертизе и удовлетворять требования и пожелания заказчиков, а главное аргументированно доказывать свои расчеты геометрически точными построениями.
Геометрические построения теней наиболее наглядны и понятны.
Источник
Сам ржу на своим вопросом. Кто нибудь тень мерил?
Короче, вот тебе научный подход 1. Онлайн калькулятор угловой высоты солнца.
http://planetcalc.ru/320/
Вводишь дату, время, регион — получаешь угол.
Жарким днем самого длинного дня года (22 июня) — угловая высота 57 градусов.
Запомним это.
То есть, в любое другое время (время года и время суток) солнце будет ниже, и угловая высота меньше.
2. Берем твой дом высотой 7 метров. Это один катет.
Расстояние до соседского огорода — другой катет.
Строим гипотенузу между концами этих катетов, и видим угол.
Тангенс угла — отношение противолежащего катета к прилежащему.
Видимо, что при угле 57 градусов тангенс равен 1,54.
То есть, в самый солнечный день года, когда солнце в наивысшей точке, тень (которая в этот день и это время самая короткая) будет иметь длину 7/1,54=4.5 метра.
Итого. В любое время года и суток тень от дома будет иметь длину БОЛЬШЕ ИЛИ РАВНОЙ 4,5 метрам от дома.
Но!
Далее вопрос в том, в какой стороне света относительно дома находится огород.
Потому что если он, например, к югу от дома — тени там не будет вообще (ночью тени не бывает).
А если, как ты пишешь, к востоку, то тень будет длинная, но уже поздно вечером, когда для овощей пофиг, есть тень или нет.
Ну так тень движется Солнце всходит утром на востоке (рано-рано солнце низко, тень длинная). Поэтому тени от объектов затеняют все то, что находится НА ЗАПАДЕ от объектов.
Потом солнце поднимается выше (тени укорачиваются) и движется через юг в сторону запада.
Самое высокое солнце (и самые короткие тени) — в обед, когда солнце прям на юге находится. Тогда затеняются участки к СЕВЕРУ от дома.
Потом солнце постепенно садится (тени опять удлинняются), солнце движется на запад, и тени соответственно на восток.
То есть, солнце движется с востока через юг на запад (описывая дугу по небу, достигая высшей точки в полдень на юге), а тени движутся с запада через север на восток, утром и вечером они длинные, в полдень они короткие.
Поэтому нельзя говорить «тень от дома 4 метра» — это имеет смысл ТОЛЬКО с указанием, в какое время суток (час-минута) и какого числа-месяца.
22 июня — самый длинный день, самое высокое солнце в полдень.
22 декабря — самый короткий день, самое низкое солнце в полдень.
Источник