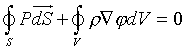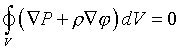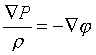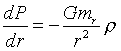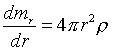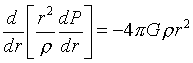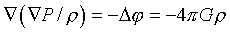Что такое гидростатическое равновесие солнца

Что такое гидростатическое равновесие солнца

Пожалуй важнейшим условием равновесия в звездах можно считать условие механического равновесия, то есть равенства сил, действующих на любой, произвольно выделенный объем в звезде. Хотя в абсолютном смысле это условие не может справедливым — практически любая звезда эволюционирует в той или иной мере, то есть меняет свой радиус, а значит существует сила, выполняющая эту работу. Однако характерное время такого измененяи в большинстве случаев столь велико (млрд. лет), что с любой разумной точностью условие равновесия следует считать выполненным. (Исключения составляют «взрывные» стадии эволюции звезды, которые весьма интересны, но очень далеки от понимания).

В классической теории эволюции принимаются в расчет только две силы, равновесие между которыми и называют гидростатическим. Первая — это давление на выделенный объем со стороны других элементов газа (то есть термодинамическое давление самой плазмы), а вторая — сила гравитационного притяжения элементов объема со стороны других элементов, составляющих звезду. Очевидно, что именно эти силы рассматриваются в гидростатике, единственным отличием является то, что поле сил тяжести в гидростатике обычно предполагается внешним.

Для получения необходимого уравнения просто приравняем все силы давления P, действующие каждый, достаточно маленький чтобы считаться плоским элемент поверхности dS, окружающей выделенный объем V, и сумму сил притяжения каждого элемента массы dm, то есть

Теперь интеграл по поверхности следует заменить на интеграл по объему. Такая замена выполняется с помощью теоремы Гаусса-Остроградского, смысл которой состоит в возможности разбить наш объем на множество маленких эелементиков «удобной» формы, например цилиндров (необязательно круговых) с осью, направленной вдоль градиента давления P. Тогда интеграл по поверхности может быть вычислен как интеграл по объему, ограниченному этой поверхностью, но уже от градиента давления (для маленького цилидра это не трудно доказать). Наше условие переходит в

Но поскольку мы никак не ограничивали выбор нашего объема, по которому ведется интегрирование, то единственный способ гарантировать выполнение этого условия — потребовать, чтобы подынтегральное выражение было равно нулю в любой точке звезды. Тогда получается векторное дифференциальное уравнение, выражающее гидростатическое равновесие звезды.

Данное уравнение справедливо для любого случая гидростатического равновесия, включая, например, неизотропное давление (нужно только правильно понимать операцию градиента от тензора давления). Однако в случае звезд, логично воспользоваться предположением о сферической симметрии звезды, тем более, что пока не видно сил, которые могли бы нарушать такую симметрию. В этом случае существует выражение для гравитационного потенциала 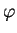(и его градиента) через массу слоев m_r, заключенных в сфере под рассматриваемой точкой — см. уравнение Пуассона. Кроме того, предположение о сферической симметрии позволяет записать дифференциальные уравнения для производных по радиусу, поскольку все остальные производные, входящие в градиент, просто равны нулю. В результате, уравнение принимает вид

с добавлением соответствующего уравнения, определяющего величину m_r

Легко понять, что из этих двух уравнений можно исключить одну неизвестную, например m_r. Правда, порядок уравнения при этом повысится до второго, а неизвестных останется все равно две.

(к этому уравнению проще всего прийти сразу из векторного условия равновесия, применяя оператор градиента и используя уравнение Пуассона

Нужно только не забыть, что под внешним градиентом в левой части стоит векторная функция, то есть он означает дивергенцию — отсюда и множитель r 2 в записи уравнения в сферических координатах).

Векторное уравнение второго порядка для известного давления P(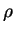) как функции плотности.

Источник

Что такое гидростатическое равновесие солнца

Пожалуй важнейшим условием равновесия в звездах можно считать условие механического равновесия, то есть равенства сил, действующих на любой, произвольно выделенный объем в звезде. Хотя в абсолютном смысле это условие не может справедливым — практически любая звезда эволюционирует в той или иной мере, то есть меняет свой радиус, а значит существует сила, выполняющая эту работу. Однако характерное время такого измененяи в большинстве случаев столь велико (млрд. лет), что с любой разумной точностью условие равновесия следует считать выполненным. (Исключения составляют «взрывные» стадии эволюции звезды, которые весьма интересны, но очень далеки от понимания).

В классической теории эволюции принимаются в расчет только две силы, равновесие между которыми и называют гидростатическим. Первая — это давление на выделенный объем со стороны других элементов газа (то есть термодинамическое давление самой плазмы), а вторая — сила гравитационного притяжения элементов объема со стороны других элементов, составляющих звезду. Очевидно, что именно эти силы рассматриваются в гидростатике, единственным отличием является то, что поле сил тяжести в гидростатике обычно предполагается внешним.

Для получения необходимого уравнения просто приравняем все силы давления P, действующие каждый, достаточно маленький чтобы считаться плоским элемент поверхности dS, окружающей выделенный объем V, и сумму сил притяжения каждого элемента массы dm, то есть

Теперь интеграл по поверхности следует заменить на интеграл по объему. Такая замена выполняется с помощью теоремы Гаусса-Остроградского, смысл которой состоит в возможности разбить наш объем на множество маленких эелементиков «удобной» формы, например цилиндров (необязательно круговых) с осью, направленной вдоль градиента давления С P. Тогда интеграл по поверхности может быть вычислен как интеграл по объему, ограниченному этой поверхностью, но уже от градиента давления (для маленького цилидра это не трудно доказать). Наше условие переходит в

Но поскольку мы никак не ограничивали выбор нашего объема, по которому ведется интегрирование, то единственный способ гарантировать выполнение этого условия — потребовать, чтобы подынтегральное выражение было равно нулю в любой точке звезды. Тогда получается дифференциальное уравнение, выражающее гидростатическое равновесие звезды.

Данное уравнение справедливо для любого случая гидростатического равновесия, включая, например, неизотропное давление (нужно только правильно понимать операцию градиента от тензора давления). Однако в случае звезд, логично воспользоваться предположением о сферической симметрии звезды, тем более, что пока не видно сил, которые могли бы нарушать такую симметрию. В этом случае существует выражение для гравитационного потенциала j (и его градиента) через массу слоев m_r, заключенных в сфере под рассматриваемой точкой — см. уравнение Пуассона. Кроме того, предположение о сферической симметрии позволяет записать дифференциальные уравнения для производных по радиусу, поскольку все остальные производные, входящие в градиент, просто равны нулю. В результате, уравнение принимает вид

с добавлением соответствующего уравнения, определяющего величину m_r

Легко понять, что из этих двух уравнений можно исключить одну неизвестную, например m_r. Правда, порядок уравнения при этом повысится до второго, а неизвестных останется все равно две.

(к этому уравнению проще всего прийти сразу из векторного условия равновесия, применяя оператор градиента и используя уравнение Пуассона

Нужно только не забыть, что под внешним градиентом в левой части стоит векторная функция, то есть он означает дивергенцию — отсюда и множитель r 2 в записи уравнения в сферических координатах).

Векторное уравнение второго порядка для известного давления как функции плотности.

Источник

Гидростатическое равновесие

Гидростатическое равновесие (англ. Hydrostatic equilibrium, hydrostatic balance ) — понятие, используемое в физике для описания равновесия гравитационных сил и направленных в противоположную сторону сил давления среды, обусловленных возникающим в направлении действия гравитации градиентом давления. [1]

Так, в частности, в воздухоплавании говорят о гидростатическом равновесии или о нулевой плавучести тела, средняя плотность которого равна плотности окружающей жидкой или газообразной среды.

Содержание

В астрофизике

Гидростатическое равновесие — равновесие в звезде между силой тяготения, направленной внутрь, и силами газового и лучистого давления, направленными наружу. [2]

В биологии

Пневматофор, воздушный пузырь — орган гидростатического равновесия у колониальных кишечнополостных — сифонофор. [3]

Плавательный пузырь — орган рыб, развивающийся как вырост передней части кишечника; может служить органом гидростатического равновесия. [4]

Примечания

1. ↑ Перевод из en-wiki
2. ↑ Хопкинс Дж. Толковый словарь ​английских терминов по астрономии и астрофизике. Изд. Мир Пер.с англ. 1980
3. ↑БСЭ. Статья «Пневматофор»
4. ↑БСЭ. Статья «Плавательный пузырь»

Источник

Для улучшения этой статьи желательно ? :

• Добавить иллюстрации.
• Найти и оформить в виде сносок ссылки на авторитетные источники, подтверждающие написанное.
• Дополнить статью (статья слишком короткая либо содержит лишь словарное определение).

Wikimedia Foundation . 2010 .

Смотреть что такое «Гидростатическое равновесие» в других словарях:

РАВНОВЕСИЕ ГИДРОСТАТИЧЕСКОЕ — устанавливающееся в жидкости при отсутствии дополнительных внешних сил. В число учтенных сил включены капиллярные силы, действующие на свободной поверхности жидкости, и статическая подъемная сила, действующая на тела, погруженные в жидкость.… … Геологическая энциклопедия

Солнечная система — в представлении художника. Масштабы расстояний от Солнца не соблюдены. Общие характеристики Возраст … Википедия

Планета — У этого термина существуют и другие значения, см. Планета (значения) … Википедия

Звёздная эволюция — в астрономии последовательность изменений, которым звезда подвергается в течение её жизни, то есть на протяжении сотен тысяч, миллионов или миллиардов лет, пока она излучает свет и тепло. В течение таких колоссальных промежутков времени… … Википедия

Мысленный эксперимент — в физике, философии и некоторых других областях знания вид познавательной деятельности, в которой ключевая для той или иной научной теории ситуация разыгрывается не в реальном эксперименте, а в воображении. Мысленный эксперимент в физике зачастую … Википедия

Планеты — (позднелат., единственное число planeta, от греч. astèr planétes блуждающая звезда) большие небесные тела, движущиеся вокруг Солнца и светящиеся отраженным солнечным светом; размеры и массы П. на несколько порядков меньше, чем у Солнца.… … Большая советская энциклопедия

Водоотлив — Так называется одна из важнейших вспомогательных работ строительного дела (см. также Горное дело), к которой приходится прибегать при устройстве оснований и фундаментов как в том случае, когда местность покрыта водою и работа ведется за… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

КАРЛИКОВЫЕ ПЛАНЕТЫ — КАРЛИКОВЫЕ ПЛАНЕТЫ, небесные тела (см. НЕБЕСНЫЕ ТЕЛА), удовлетворяющие следующим условиям: • вращаются по орбите вокруг Солнца; • имеют достаточную массу для того, чтобы под действием сил гравитации поддерживать гидростатическое равновесие и… … Энциклопедический словарь

Спутники Урана — Сравнительные размеры шести самых известных спутников Урана. Слева направо: Пак, Миранда, Ариэль, Умбриэль, Титания и Оберон. Спутники Урана естественные спутники планеты Уран. Известно 27 спутников. Вс … Википедия

Церера (карликовая планета) — У этого термина существуют и другие значения, см. Церера. Церера … Википедия

Источник

Гидростатическое равновесие

Из Википедии, бесплатной энциклопедии

Гидростатическое равновесие (англ. Hydrostatic equilibrium, hydrostatic balance ) — понятие, используемое в физике для описания равновесия гравитационных сил и направленных в противоположную сторону сил давления среды, обусловленных возникающим в направлении действия гравитации градиентом давления.

Так, в частности, в воздухоплавании говорят о гидростатическом равновесии или о нулевой плавучести тела, средняя плотность которого равна плотности окружающей жидкой или газообразной среды.

Содержание

В астрофизике [ править | править код ]

Гидростатическое равновесие — равновесие в звезде между силой тяготения, направленной внутрь, и силами газового и лучистого давления, направленными наружу [1] .

В биологии [ править | править код ]

Пневматофор, воздушный пузырь — орган гидростатического равновесия у колониальных кишечнополостных — сифонофор [2] .

Плавательный пузырь — орган рыб, развивающийся как вырост передней части кишечника; может служить органом гидростатического равновесия [3] .

В технике [ править | править код ]

Система погружения и всплытия подводной лодки обеспечивает регулирование ее гидростатического веса (плавучести), обеспечивая в том числе гидродинамическое равновесие при нахождении лодки на постоянной глубине.

Источник