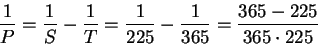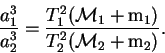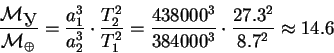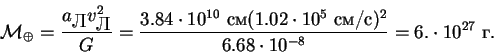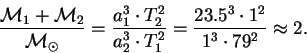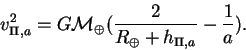Конфигурация планет и синодический период
Как известно, все объекты в нашей системе вращаются вокруг Солнца. Но не многие знают, какая вообще существует конфигурация планет Солнечной системы. Вот как раз об этом сегодня и пойдёт речь.
В действительности планетные тела разделяют на нижние и верхние.
Нижние или внутренние: Венера и Меркурий имеют орбиты, расположенные ближе к центральному светилу, чем земная.
А вот у верхних (внешних), наоборот, орбита находится за орбитой Земли. Собственно, к ним относятся Марс, Сатурн, Нептун, Уран и Юпитер.
Не стоит упускать из виду, что условия видимости небесных, в том числе и планетных тел изменяется с течением времени. Например, одни видны с Земли только утром или вечером, а другие можно наблюдать ночью.
Как оказалось, на условия видимости небесных тел с Земли влияет расстояние от Солнца, а также их орбитальные скорости. Но учёные смогли выделить некоторое типичное взаиморасположение объектов.

Конфигурация планет Солнечной системы — это характерное взаимное расположение Солнца и планет на небесной сфере.
В зависимости от положения планеты относительно Солнца, освещающего её, и непосредственно Земли, откуда за ней наблюдают, видимость в определённой конфигурации меняется.
Между прочим, видимое передвижение верхних планет происходит без смены фаз. Правда, если они достигают диаметрально противоположной точки, то это уже называется противостоянием. По сути, они повернуты к нам освещённой стороной и в этот момент их лучше всего видно.
В то же время, для внутренних планет выделяют два вида соединений: нижние и верхние.
Стоит отметить, что соединение — это расположение небесных объектов с точкой совпадения их долготы во время наблюдения за ними с Земли. Другими словами, земной наблюдатель видит точку соединения, например, планеты и Солнца.
Причем в нижнем соединении планетное тело наиболее приближено к нам, а в верхнем, напротив, растёт удалённость от нас. Мы не можем заметить их при этом, поскольку либо их скрывает светило, либо его лучи.
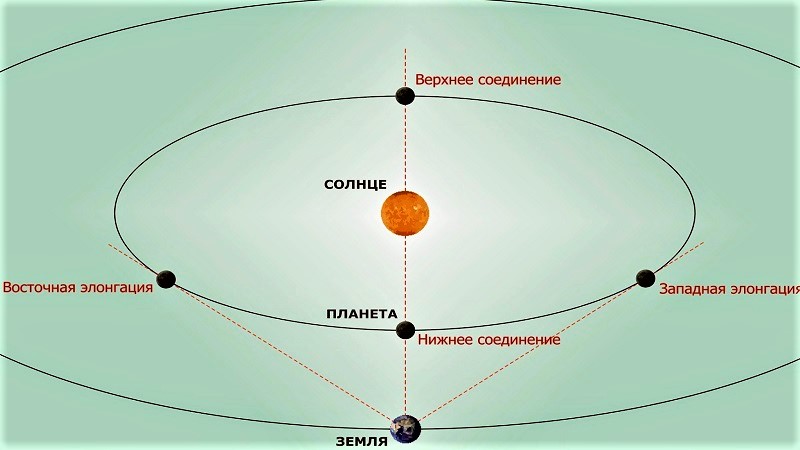
Синодический период
Помимо этого, есть такое положение планетных объектов, которое определяется как максимально угловое расстояние между ними и Солнцем. К слову, оно называется элонгация.
Для примера, с нашей планеты заметно перемещение Меркурия и Венеры, которое сопровождается сменой фаз. Поскольку они движутся недалеко от Солнца, и мы можем наблюдать их максимальное удаление от него. А вот в зависимости от направления их движения различают утреннюю (западную) и вечернюю (восточную) элонгацию.
По данным учёных, угловое расстояние планетных тел может составлять от 0 до 180 градусов. Когда угол между ними и земной точки, направленной на них равен 90 градусов, планета находится в квадратуре. Она так же, как элонгация, бывает западной и восточной.
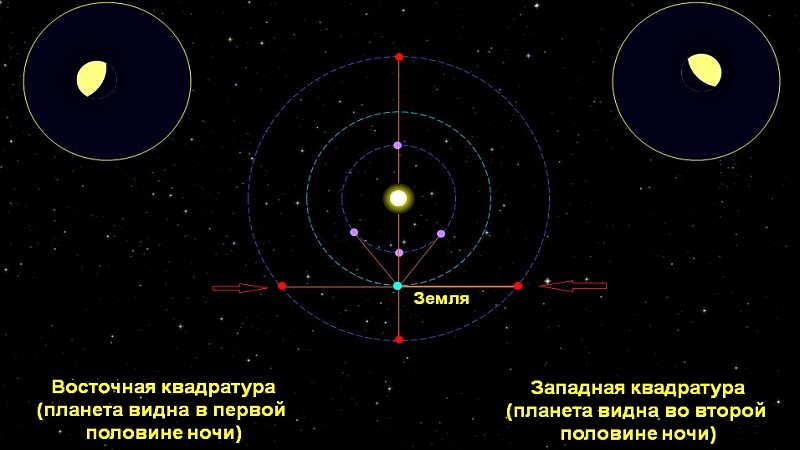
В результате того, что все тела вращаются вокруг одного главного светила, та или иная конфигурация планет Солнечной системы периодически повторяется. Между тем, у каждой планеты этот период свой. И он зависит не только от вращения вокруг Солнца, но и от её собственного движения.
Синодический период планет — это интервал времени между двумя одинаковыми конфигурациями этих планет. К примеру, между нижними соединениями.
Так как синодические периоды обращения планет различные, учёные определили их для каждой отдельно.
Итак, в годах данный промежуток составляет: Меркурий — 0,317, Венера — 1,599, Марс — 2,135, Юпитер — 1,092, Сатурн — 1,035, Уран — 1,012 и Нептун — 1,006.
Не стоит путать, синодический и сидерический периоды. Первый отражает время между взаимным положением Солнца и планет. А второй промежуток, за который совершается полный оборот вокруг солнца.
Проще говоря, сидерический период — время, затраченное на одно обращение планеты вокруг Солнца. Также его называют годом.
В зависимости от объекта различают земной год, юпитерианский год и так далее.

На самом деле, конфигурация планет Солнечной системы знакома людям ещё с древних времён. Как только начали обращать внимание на небо, на звёзды, на их движение и перемещение по небесной сфере.
Источник
Чем дальше планета от солнца тем ее сидерический период меньше
Современная формулировка первого закона дополнена так: в невозмущенном движении орбита движущегося тела есть кривая второго порядка – эллипс, парабола или гипербола.
В отличие от двух первых, третий закон Кеплера применим только к эллиптическим орбитам.
Скорость движения планеты в перигелии
где v c – средняя или круговая скорость планеты при r = a . Скорость движения в афелии
Кеплер открыл свои законы эмпирическим путем. Ньютон вывел законы Кеплера из закона всемирного тяготения . Для определения масс небесных тел важное значение имеет обобщение Ньютоном третьего закона Кеплера на любые системы обращающихся тел.
Комета Галлея обращается вокруг Солнца с периодом обращения 76 лет. Нептун имеет период обращения 164,8 лет. Кто из них более удален от Солнца в точке афелия своей орбиты?
аГ = 17,8 а.е., q = 0,59 а.е. Комета удаляется от Солнца на 2∙17,8 – 0,59 = 35,01 а.е.
Большая полуось Нептуна а Нептуна = 30 а.е.
Ответ. Дальше от Солнца в афелии находится комета Галлея.
Комета Темпеля имеет вытянутую орбиту, ее перигелийное расстояние 1,37 а.е., период обращения вокруг Солнца Т = 5,26 лет. Найти наибольшее расстояние от Солнца, большую полуось и эксцентриситет кометы Темпеля.
Большую полуось можно найти из третьего закона Кеплера T 2 / T 2 = a 3 / a 3 ;
где Т = 1 год, а = 1 а.е.
Наибольшее расстояние от Солнца – афелий орбиты кометы Q = 2 a – q = 4,63 а.е.
Ответ. Эксцентриситет е = 0,54, афелий Q = 4,63 а.е., большая полуось а = 3,0 а.е.
В XVIII веке была подмечена закономерность, которая в настоящее время называется правилом Тициуса–Боде. Средние расстояния от планет до Солнца выражаются, согласно этому правилу следующей формулой: а = 0,1∙(3∙2 n + 4) а.е.
В 1993 году у пульсара PSR В 1257+12 были найдены три планеты. Все они находятся на расстояниях, пропорциональных (но не равных) расстояниям от Солнца Меркурия, Венеры и Земли (0,30/0,72/1,0). Что изменится в формулировке правила Тициуса – Боде для данной системы? Ответ. Коэффициент перед скобкой.
Замечено, что противостояния некоторой малой планеты повторяются через 2 года. Чему равна большая полуось ее орбиты?
Понятие противостояния определено только для внешних планет:
сидерический период Т = 2 года, а по третьему закону Кеплера T 2 / T 2 = a 2 / a 2 , отсюда большая полуось орбиты а = 1,59 а.е. Внешняя планета находится за орбитой Марса.
Сколько времени нужно лететь с Земли на Марс по гомановской орбите в космическом корабле, перигелийное расстояние которого равно расстоянию от Земли до Солнца, а афелийное расстояние – расстоянию от Марса до Солнца?
По третьему закону Кеплера
большая полуось орбиты космического корабля
Для Земли T = 1 год, a = 1 а.е., поэтому T = 1,4 года, а время полета
Контрольная работа. Конфигурации планет. Законы Кеплера. Вариант № 1
Какие небесные явления происходят при данных конфигурациях небесных тел:
1. Если А — планета Марс; В — Земля; С — Солнце, произойдет:
1) солнечное затмение; 2) лунное затмение; 3) противостояние; 4) верхнее соединение; 5) нижнее соединение; 6) покрытие.
2. Если А — Земля; В — Солнце; С — планета Венера, произойдет:
1) солнечное затмение; 2) лунное затмение; 3) противостояние;
4) верхнее соединение; 5) нижнее соединение; 6) покрытие.
3. В нижнем соединении не могут находиться … планеты:
1) внешние; 2) внутренние; 3) нижние планеты.
4. Рядом с Луной во время полнолуния могут быть видны … планеты:
1) только внутренние; 2) только внешние; 3) как внутренние, так и внешние; 4) во время полнолуния рядом с Луной планеты нельзя наблюдать.
5. Максимальное угловое отклонение от Солнца наблюдается у:
1) Венеры; 2) Меркурия; 3) Марса.
6. Как меняется значение скорости движения кометы при ее перемещении от перигелия к афелию?
1) не изменяется; 2) увеличивается; 3) уменьшается; 4) скорость кометы не зависит от положения на орбите.
7. По каким траекториям движутся космические аппараты к Луне от Земли?
1) по параболе; 2) по эллипсу, в одном из фокусов которого находится Земля; 3) по эллипсу, в одном из фокусов которого находится Солнце; 4) по прямой.
Контрольная работа. Конфигурации планет. Законы Кеплера. Вариант № 2
Какие небесные явления происходят при данных конфигурациях небесных тел:
1. Если А — планета Юпитер; В — Земля; С — Солнце, произойдет:
1)солнечное затмение; 2)лунное затмение; 3)верхнее соедениние; 4) противостояние; 5) нижнее соединение; 6) покрытие.
2. Если А — Земля; В — Солнце; С — планета Меркурий, произойдет:
1) солнечное затмение; 2) лунное затмение; 3) верхнее соединение; 4) противостояние; 5) нижнее соединение; 6) покрытие.
3. В нижнем соединении могут находиться … планеты:
1) внешние; 2) внутренние; 3) верхние планеты.
4. Рядом с Луной во время полного лунного затмения могут быть видны … планеты:
1) только внутренние; 2) только внешние; 3) как внутренние, так и внешние; 4) во время полнолуния рядом с Луной планеты нельзя наблюдать.
5. Максимальное угловое отклонение от Солнца наблюдается у:
1) Венеры; 2) Меркурия; 3) Юпитера.
6. Как меняется сидерический период обращения планет-гигантов вокруг Солнца с удалением от него?
1) Чем дальше планета от Солнца, тем ее сидерический период больше.
2) Чем дальше планета от Солнца, тем ее сидерический период меньше.
3) Период обращения планет-гигантов не зависит от их расстояния до Солнца.
4) Период обращения планет-гигантов вокруг Солнца равен периоду их обращения вокруг оси.
7. По каким траекториям движутся космические аппараты к Луне от Земли?
1) по параболе; 2) по эллипсу, в одном из фокусов которого находится Земля; 3) по эллипсу, в одном из фокусов которого находится Солнце; 4) по прямой.
Источник
Чем дальше планета от солнца тем ее сидерический период меньше
Планеты Солнечной системы обращаются вокруг Солнца по эллиптическим орбитам (см.законы Кеплера) и делятся на две группы. Планеты, которые расположены ближе к Солнцу, чем Земля, называются нижними. Это Меркурий и Венера. Планеты, которые расположены дальше от Солнца, чем Земля, называются верхними. Это Марс, Юпитер, Сатурн, Уран, Нептун и Плутон.
Планеты в процессе обращения вокруг Солнца могут располагаться относительно Земли и Солнца произвольным образом. Такое взаимное расположение Земли, Солнца и планеты называется конфигурацией. Некоторые из конфигураций являются выделенными и носят специальные названия (см. рис. 19).
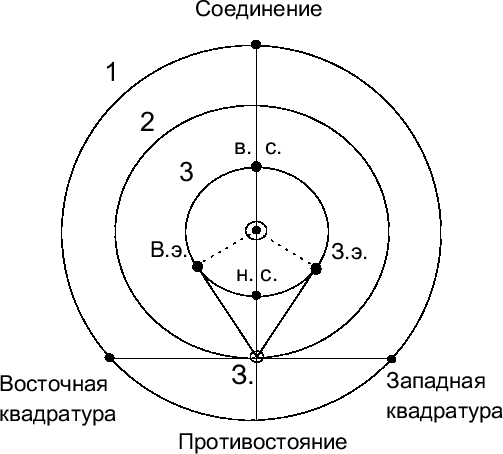 |
| Рис. 19. Конфигурации планет. 1 — орбита верхней планеты, 2 — орбита Земли (З.), 3 — орбита нижней планеты. Конфигурации нижней планеты: в.с. — верхнее соединение, н.с. — нижнее соединение, В.э. — наибольшая восточная элонгация, З.э. — наибольшая западная элонгация. |
Нижняя планета может располагаться на одной линии с Солнцем и Землей: либо между Землей и Солнцем — нижнее соединение, либо за Солнцем — верхнее соединение. В момент нижнего соединения может произойти прохождение планеты по диску Солнца (планета проецируется на диск Солнца). Но из-за того, что орбиты планет не лежат в одной плоскости, такие прохождения случаются не каждое нижнее соединение, а достаточно редко. Конфигурации, при которых планета при наблюдении с Земли находится на максимальном угловом удалении от Солнца (это наиболее благоприятные периоды для наблюдения нижних планет), называются наибольшими элонгациями, западной и восточной.
Верхняя планета также может находиться на одной линии с Землей и Солнцем: за Солнцем — соединение, и по другую сторону от Солнца — противостояние. Противостояние — это самое благоприятное время для наблюдения верхней планеты. Конфигурации, при которых угол между направлениями с Земли на планету и на Солнце равен 90 o , называются квадратурами, западной и восточной.
Промежуток времени между двумя последовательными одноименными конфигурациями планеты называется ее синодическим периодом обращения P, в отличие от истинного периода ее обращения относительно звезд, называемого поэтому сидерическим S. Разница между этими двумя периодами возникает из-за того, что Земля тоже обращается вокруг Солнца с периодом T. Синодический и сидерический периоды связаны между собой:
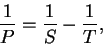 | (26) |
для нижней планеты, и
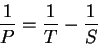 | (27) |
10.2. Законы Кеплера
Законы, по которым планеты обращаются вокруг Солнца, были эмпирически (т.е. из наблюдений) установлены Кеплером, а затем теоретически обоснованы на основе закона всемирного тяготения Ньютона.
Первый закон. Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце.
Второй закон. При движении планеты ее радиус-вектор описывает равные площади за равные промежутки времени.
Третий закон. Квадраты сидерических времен обращений планет относятся друг к другу как кубы больших полуосей их орбит (как кубы их средних расстояний от Солнца):
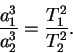 | (28) |
Третий закон Кеплера является приближенным, из закона всемирного тяготения был получен уточненный третий закон Кеплера:
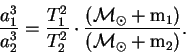 | (29) |
Третий закон Кеплера выполняется с хорошей точностью только потому, что массы планет много меньше массы Солнца 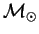
Эллипс — это геометрическая фигура (см. рис. 20), у которой есть две главные точки — фокусы F1, F2, и сумма расстояний от любой точки эллипса до каждого из фокусов есть величина постоянная, равная большой оси эллипса. У эллипса есть центр O, расстояние от которого до наиболее удаленной точки эллипса называется большой полуосью a, а расстояние от центра до самой ближайшей точки называется малой полуосью b. Величина, которая характеризует сплюснутость эллипса, называется эксцентриситетом e:
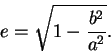 | (30) |
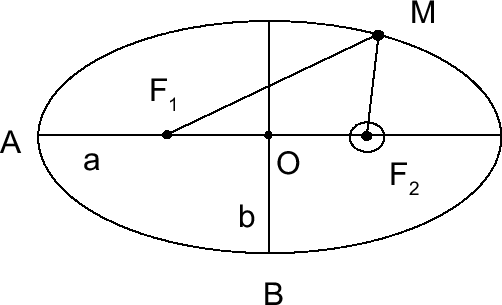 |
| Рис. 20. Орбита планеты — эллипс |
Окружность является частным случаем эллипса (e=0).
Расстояние от планеты до Солнца изменяется от наименьшего, равного
(эта точка орбиты называется перигелием) до наибольшего, равного
(эта точка орбиты называется афелием).
10.3. Движение искусственных небесных тел
Движение искусственных небесных тел подчиняется тем же законам, что и естественных. Тем не менее, необходимо отметить ряд особенностей.
Главное — размеры орбит искусственных спутников, как правило, сравнимы с размерами планеты, вокруг которой они обращаются, поэтому часто говорят о высоте спутника над поверхностью планеты (рис.21). При этом надо учитывать, что в фокусе орбиты спутника находится центр планеты.
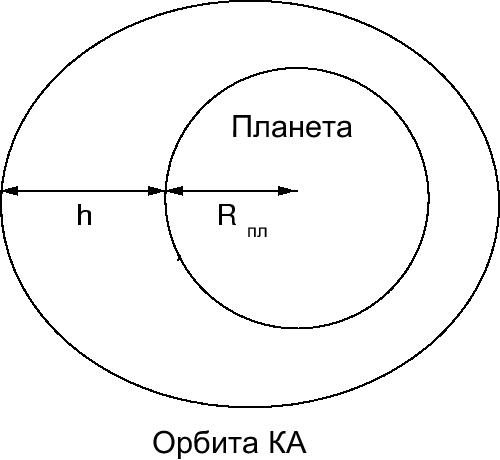 |
| Рис. 21. Орбита искусственного спутника планеты |
Для искусственных спутников вводят понятие первой и второй космической скорости.
Первая космическая скорость или круговая скорость — это скорость кругового орбитального движения у поверхности планеты на высоте h:
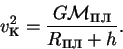 | (33) |
Это минимально необходимая скорость, которую необходимо придать космическому аппарату, чтобы он стал искусственным спутником данной планеты. Для Земли у поверхности vк = 7.9 км/сек.
Вторая космическая скорость или параболическая скорость — это скорость, которую необходимо придать космическому аппарату, чтобы он мог покинуть сферу притяжения данной планеты по параболической орбите:
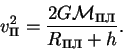 | (34) |
Для Земли вторая космическая скорость равна 11.2 км/сек.
Скорость небесного тела в любой точке эллиптической орбиты на расстоянии R от тяготеющего центра может быть рассчитана по формуле:
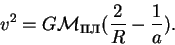 | (35) |
Здесь повсюду 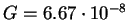
4. Может ли случиться прохождение Марса по диску Солнца? Прохождение Меркурия? Прохождение Юпитера?
5. Можно ли увидеть Меркурий вечером на востоке? А Юпитер?
46. Противостояние Марса произошло 19 мая. В каком созвездии он был виден?
Решение: Орбиты всех планет лежат приблизительно в одной плоскости, поэтому планеты двигаются по небесной сфере примерно по эклиптике. В момент противостояния прямые восхождения Марса и Солнца отличаются на 180 o : 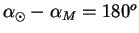
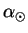
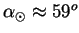
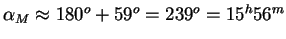
47. (398) Наилучшая вечерняя видимость Венеры (наибольшее ее удаление к востоку от Солнца) была 5 февраля. Когда в следующий раз наступила видимость Венеры в тех же условиях, если ее сидерический период обращения равен 225 d ?
Решение: Наилучшая вечерняя видимость Венеры наступает во время ее восточной элонгации. Следовательно, следующая наилучшая вечерняя видимось наступит во время следующей восточной элонгации. А промежуток времени между двумя последовательными восточными элонгациями равен синодическому периоду обращения Венеры и легко может быть вычислен:
или P=587 d . Значит, следующая вечерняя видимость Венеры в тех же условиях наступит через 587 дней, т.е. 14-15 сентября следующего года.
48. (663) Определить массу Урана в единицах массы Земли, сравнивая движение Луны вокруг Земли с движением спутника Урана — Титанией, обращающегося вокруг него с периодом 8 d .7 на расстоянии 438 000 км. Период обращения Луны вокруг Земли 27 d .3, и среднее расстояние ее от Земли составляет 384 000 км.
Решение: Для решения задачи необходимо воспользоваться третьим уточненным законом Кеплера. Так как для любого тела массой m, обращающегося вокруг другого тела массой 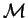
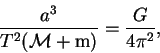 | (36) |
то мы имеем право для любой пары обращающихся друг вокруг друга небесных тел записать равенство:
Принимая за первую пару Уран с Титанией, а за вторую — Землю с Луной, а также пренебрегая массой спутников по сравнению с массой планет получим:
49. Принимая орбиту Луны за окружность и зная орбитальную скорость движения Луны vЛ = 1.02 км/с, определить массу Земли.
Решение: Вспомним формулу для квадрата круговой скорости (35) и подставим среднее расстояние Луны от Земли aЛ (см. предыдущую задачу):
50. Вычислить массу двойной звезды 
Решение: Решение этой задачи аналогично решению задачи о массе Урана. Только при определении масс двойных звезд их сравнивают с парой Солнце-Земля и выражают их массу в массах Солнца.
51.(1210) Вычислите линейные скорости космического корабля в перигее и апогее, если над Землей в перигее он пролетает на высоте 227 км над поверхностью океана и большая ось его орбиты составляет 13 900 км. Радиус и масса Земли 6371 км и 6.0 10 27 г.
Решение: Рассчитаем расстояние от спутника до Земли в апогее (наибольшем расстоянии от Земли). Для этого необходимо зная расстояние в перигее (наименьшее расстояние от Земли) вычислить эксцентриситет орбиты спутника по формуле (31) и затем определить искомое расстояние используя формулу (32). Получим ha = 931 км.
Далее воспользуемся формулой (35) для вычисления скорости тела на любом расстоянии от тяготеющего центра и вычислим скорость в перигее и апогее:
52. (393) Синодический период обращения одного из астероидов составляет 3 года. Каков звездный период его обращения около Солнца?
53. (400) Найти среднее суточное движение Меркурия по орбите (величину дуги орбиты, которую он проходит за земные сутки), если синодический период его обращения вокруг Солнца равняется 115.88 суткам.
54. (417) С какой видимой угловой скоростью Венера пересекает диск Солнца? Сколько времени длится ее прохождение по диску Солнца, если оно центральное? Расстояние Венеры от Солнца 0.723 а.е., синодический период обращения 584 дня, угловой диаметр Солнца 32′.
55. (662) Вычислить массу Нептуна относительно массы Земли, зная, что его спутник отстоит от центра планеты на 354 000 км и период его обращения равен 5 суткам 21 часу.
56. (671) Какова должна быть масса Земли (по сравнению с действительной), чтобы Луна обращалась вокруг нее с современным периодом, но на вдвое большем расстоянии?
57. (675) Удержало ли бы Солнце нашу Землю, несущуюся вокруг него со скоростью 29.76 км/сек, если бы масса Солнца внезапно уменьшилась в два раза?
58. (1214) Для целей связи нужны спутники, которые «висят» над одной и той же точкой Земли, так называемые геостационарные спутники. На какой высоте над поверхностью Земли они должны находиться?
59. (1217) Космонавты облетают Луну по круговой орбите на высоте 50 км. На сколько им надо увеличить двигателями скорость своего космического корабля, чтобы вернуться на Землю? Радиус Луны 1738 км, а ее масса составляет 1/81 массы Земли.
Источник