Ближайшую точку солнца называют

Тест по астрономии на тему «Законы Кеплера». 10-11 класс

Учитель: Елакова Галина Владимировна.

Место работы: МБОУ «СОШ №7» г. Канаш Чувашской Республики

Тест по теме: «Законы Кеплера – законы движения небесных тел».

Проверка и оценка знаний – обязательное условие результативности учебного процесса. В соответствии общими целями обучения и развития учащихся, требованиями ФГОС по астрономии к уровню подготовки выпускников школы проверяется не только овладение определенной системой понятий и законов, но и освоение экспериментальных методов познания окружающего мира.

Тестовый тематический контроль может проводиться устно или письменно, фронтально или по группам с разным уровнем подготовки. Такая проверка экономна по времени, обеспечивает индивидуальный подход.

Данный тест позволяет быстро и объективно оценить уровень подготовки учащихся, выявить типичные ошибки и определить пробелы в знаниях. Тест содержит 10 вопросов, на каждый вопрос предлагается несколько ответов, из которых учащимся нужно выбрать один правильный. Учитывая неоднородность класса и индивидуальные способности обучающихся, учитель может предложить некоторые задачи выборочно. В течение учебного года ученик может переходить с одного уровня сложности на другой, более высокий. Тест рассчитан на выполнение в течение 10-15минут. Выполняя тестовые задания, учащиеся должны пользоваться приложениями, данными в учебнике, брать из таблиц нужные для решения задач величины. Задачи и задания, содержащие в тестовых работах, направлены на формирование умений, требуемых программой, а также на контроль за степенью их сформированности и уровнем знаний учащихся по основным вопросам курса астрономии. Оценка знаний учащихся по итогам выполнения теста может производиться по шкале:

— оценка «5» ставится, если число правильных ответов составляет от 8 — 10;

оценка «4» — от 6 — 7 заданий;

оценка «3» — от 4- 5 заданий.

1. Ближайшую к Солнцу точку орбиты называют…

А) Афелием;
Б) Перигелием;

2. Ближайшая к Земле точка орбиты Луны или какого-нибудь искусственного спутника Земли называется…

А) Перигелием;
Б) Апогеем;
В) Перигеем.

3. Объясните с помощью закона Ньютона, почему спутники удерживаются на орбитах около своих планет.

А) На своей орбите около планеты спутник удерживается вследствие сложения двух движений – прямолинейного движения по инерции и движения к планете, вызываемого ее притяжением.
Б) На своей орбите около планеты спутник удерживается вследствие прямолинейного движения по инерции.
В) На своей орбите около планеты спутник удерживается вследствие движения к планете, вызываемого ее притяжением.
4. Приведите два факта, которые подтверждают аккреционную (аккреция – конденсация вещества) теорию образования Солнечной системы.

А) Все планеты обращаются вокруг Солнца в одном и том же направлении. Орбиты всех планет лежат почти в плоскости эклиптики.
Б) Планеты гиганты обращаются вокруг Солнца в одном направлении, а планеты земной группы – в другом направлении.
В) Часть планеты Солнечной системы обращаются вокруг Солнца с запада на восток, а другая часть – наоборот. Орбиты всех планет лежат почти в плоскости эклиптики.
5. Как меняется значение скорости движения планеты при ее перемещении от перигелия к афелию?

А) Уменьшается согласно второму закону Кеплера: в перигелии она минимальна, а в афелии максимальна.

Б) Увеличивается согласно второму закону Кеплера: в перигелии она максимальна, а в афелии минимальна.

В) Уменьшается согласно второму закону Кеплера: в перигелии она максимальна, а в афелии минимальна.

6. Почему движение планет происходит не в точности по законам Кеплера?

А) В Солнечной системе не одна планета, а много, и каждая из них испытывает со стороны других возмущения.
Б) В Солнечной системе не одна планета, а много, и каждая из них движется петлеобразно.
В) В Солнечной системе не одна планета, а много, и каждая из них практически имеет несколько спутников.

7. Как зависят периоды обращения спутников от массы планет?

А) Чем меньше масса, тем меньше периоды спутников.
Б) Чем больше масса , тем больше периоды спутников.
В) Чем больше масса, тем меньше периоды спутников.

8. Как далеко от Солнца находится планета, если ее орбитальный период составляет 8 лет?

9. Большая полуось орбиты Марса 1,5 а.е. Чему равен звездный период его обращения вокруг Солнца?

А) 29, 3 лет
Б) 18,65 года.
В) 1,86 года.

10. Когда Земля (4 января) находится в перигелии, Солнце движется по небу с угловой скоростью 61′ в сутки, а 4 июля, когда Земля в афелии, — 57′ в сутки. Определите эксцентриситет земной орбиты.

1. Наиболее удаленную к Солнцу точку называют…

А) Афелием;
Б) Перигелием;

2. Наиболее удаленная к Земле точка орбиты Луны или какого-нибудь искусственного спутника Земли называется…

А) Перигелием;
Б) Апогеем;
В) Перигеем.

3. Что удерживает планеты на их орбитах вокруг Солнца?

А) На орбитах вокруг Солнца планета удерживается вследствие сложения двух движений – прямолинейного движения по инерции и движения к планете, вызываемого ее притяжением.
Б) На орбитах вокруг Солнца планета удерживается вследствие сложения прямолинейного движения по инерции и движения по направлению к Солнцу под действием силы солнечного притяжения.
В) На своей орбите около Солнца планета удерживается вследствие прямолинейного движения по инерции.

4. Как меняется значение скорости движения планеты при ее перемещении от афелия к перигелию?

А) В афелии скорость планеты максимальная, затем она возрастает и в перигелии становится минимальной.
Б) В афелии скорость планеты минимальная, затем она возрастает и в перигелии становится максимальной.
В) В афелии скорость планеты минимальная, затем она возрастает и в перигелии становится равной нулю.
5. Как происходит видимое движение планет?

А) Планеты перемещаются петлеобразно.
Б) Планеты перемещаются по окружности.
В) Планеты перемещаются по эллипсу.

6. В чем состояло уточнение Ньютоном третьего закона Кеплера?

А) Во введении в формулу третьего закона Кеплера множителя, учитывающего суммарную массу Солнца и планеты.
Б) Во введении в формулу второго закона Кеплера множителя, учитывающего суммарную массу Солнца и планеты.
В) Во введении в формулу первого закона Кеплера множителя, учитывающего суммарную массу Солнца и планеты.
7. При каких условиях движение небесных тел будет происходить в точности по законам Кеплера?

А) Если в Солнечной системе одна планета.

Б) Если в Солнечной системе не одна планета, а много, и каждая из них испытывает со стороны других возмущения.
В) В случае, если существуют лишь два взаимно притягивающихся тела.

8 . Большая полуось орбиты Юпитера 5 а.е. Каков звездный период его обращения вокруг Солнца?

А) 11,5 года
Б) 29, 3 лет
В) 1, 86 лет

9. Звездный период обращения Юпитера вокруг Солнца составляет 12 лет. Каково среднее расстояние Юпитера до Солнца?

10. Комета Галлея имеет эксцентриситет е=0,967 и период обращения 76 лет. Определите большую полуось орбиты, перигельное и афельное расстояния кометы. Где расположен афелий кометы?

Вариант I : 1- Б; 2 – В;3 – А;4 – А;5 – В;6 – А;7 – В;8 — В;9 — В;

Вариант II : 1- А;2 – Б;3 – Б; 4 – Б;5 – А;6 – А;7 – В;8 – А; 9 — А;

Решение задачи №8: Согласно третьему закону Кеплера, а ³= Т ² , где а — расстояние планеты от Солнца, Т – орбитальный период планеты в годах находится из наблюдений.

а ³= Т ² , а ³= 8 ² = 64, значит, а = = 4 а.е.

Решение задачи №9: Согласно третьему закону Кеплера, а ³= Т ² , где а — расстояние планеты от Солнца, Т – орбитальный период планеты в годах находится из наблюдений.

Т = Т =³ года = 1, 86 года.

Решение задачи №10: Пусть в перигелии V п = 61′ в сутки, в афелии V а = 57′ в сутки; по третьему закону Кеплера и с учетом угловой скорости в афелии и перигелии имеем

Решение задачи №8: Согласно третьему закону Кеплера, а ³= Т ² , где а — расстояние планеты от Солнца, Т – орбитальный период планеты в годах находится из наблюдений.

а ³= Т ² , значит, Т =³ года = 1, 86 года.

Решение задачи №9: Если принять расстояние Земли от Солнца и период обращения за 1, то по третьему закону Кеплера а =² = 5 а.е.

Решение задачи №10: Используя третий закон Кеплера значение большой полуоси Земной орбиты, определяем перигельное q и афельное Q расстояния; где а для Земли 1а.е., Т з земли 1 год, Т г = 76 лет.

T²/T з ² = а³/a з ³; а = = 17,942 а.е.

Q = а(1 + е) = 17,942(1 + 0, 967) = 35,292 а.е.

1. Б.А. Воронцов-Вильяминов, Е.К. Страут; «Астрономия», Издательство «Дрофа».

2. Левитан Е.П., 2Астрономия», М.: «Просвещение»,1994.

3. Малахова Г.И, Страут Е.К., «Дидактический материал по астрономии», М.: «Просвещение»,1989.

4. Моше Д.:»Астрономия»: Кн. для учащихся. Перевод с англ./Под ред. А.А. Гурштейна;

5. Тульчинский М.Е. «Занимательные задачи — парадоксы и софизмы по физике», М.: «Просвещение».

6. Перельман Я. И. «Занимательная астрономия», — Д.: ВАП, 1994.

7. Тихомирова С.А., «Физика» 11 класс, М.: Мнемозина, 2008.

8. Шеффер О.Р., Шахматова В.В., «Методика изучения астрономии в курсе физики основной и средней(полной) школе»; Челябинск, Издательство: ИИУМЦ «Образование», 2010.

Источник

Ближайшая к Солнцу точка орбиты небесного тела, обращающегося вокруг него (астрономическое)

Ответ на вопрос Ближайшая к Солнцу точка орбиты небесного тела, обращающегося вокруг него (астрономическое), в слове 9 букв:
Перигелий

Определение слова Перигелий в словарях

Перигелий Периге́лий ( «пери» — вокруг, около, возле, «гелиос» — Солнце) — ближайшая к Солнцу точка орбиты планеты или иного небесного тела Солнечной системы. Антонимом перигелия является афе́лий (апоге́лий) — наиболее удалённая от Солнца точка орбиты.

Особенно досаждал нам этот самый перигелий Меркурия, будь он неладен со всем его ливером (по выражению Кольки, опять-таки).

Да мы-то еще бы ничего, особенно Урмас, а вот Лидочке перигелий ужасно не нравился, она даже сказала как-то с ясными глазами:

Четыре тысячи миль смертоносной жары — и только для того, чтобы какой-нибудь молодчик подкатил следом за вами, использовал все ваши данные и прикарманил вашу славу, проделав спустя сорок четыре дня тот же маршрут в перигелий ?

Я хочу форсировать Солнечную без дураков, — он резко придвинулся ко мне. — Я намерен преодолеть Солнечную в перигелий и притом — по поверхности.

В перигелий это самое раскаленное место во всей нашей солнечной системе, если не считать поверхности самого Солнца.

Температура на Солнечной стороне Меркурия достигает в перигелий плюс 410 градусов по Цельсию; а на Ночной стороне почти всегда постоянна минус 244 градуса.

Франциска, — «люди духа», viri spirituales, как сами себя называют они,[11] а лучшие из лучших могли бы назвать себя «людьми Духа Святого»; люди же XX века, если не лучшие, то и не худшие, — «люди вещества», «материалисты», как тоже сами себя называют они, а худших можно бы назвать «людьми Духа Нечистого»: вот один из двух очевиднейших признаков нашей с людьми XIII века «антиподности», «обратности», а другой, столь же очевидный, — то, что в планетно-круговом движении человечества по орбите всемирной истории крайняя точка приближения к солнцу. — Христу, перигелий , достигнута, после двух первых веков христианства, в XIII веке, а точка отдаления, такая же крайняя, апогелий, — в XX веке.

Тип Атона, цифро-буквенное обозначение такое-то, орбита находится внутри орбиты Земли, а перигелий аж внутри орбиты Венеры.

Если соединить перигелий орбиты Марса с Солнцем прямой линией, то она пересечет орбиту Земли в той точке, которую Земля проходит 29 августа.

Источник

Видимое годовое движение солнца на небесной сфере

Истинное движение Земли — Видимое годовое движение Солнца на небесной сфере — Небесный экватор и плоскость эклиптики — Экваториальные координаты Солнца в течение года

Истинное движение Земли

Чтобы понять принцип видимого движения Солнца и других светил на небесной сфере, рассмотрим сперва истинное движение Земли. Земля является одной из планет солнечной системы. Она непрерывно вращается вокруг своей оси.

Период вращения ее равен одним суткам, поэтому наблюдателю, находящемуся на Земле, кажется, что все небесные светила обращаются вокруг Земли с востока на запад с тем же периодом.

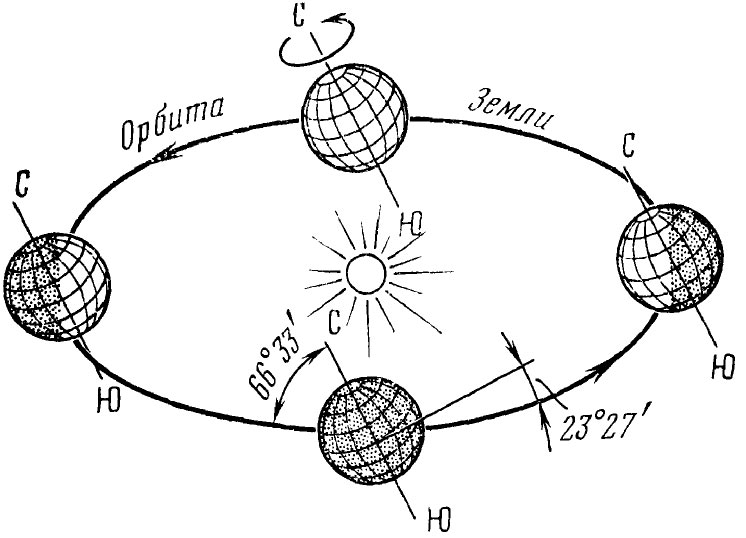
Наклон оси вращения Земли к плоскости орбиты

Но Земля не только вращается вокруг своей оси, но и обращается также вокруг Солнца по эллиптической орбите. Полный оборот вокруг Солнца она совершает за один год. Ось вращения Земли наклонена к плоскости орбиты под углом 66°33′. Положение оси в пространстве при движении Земли вокруг Солнца все время остается почти неизменным. Поэтому Северное и Южное полушария попеременно бывают обращены в сторону Солнца, в результате чего на Земле происходит смена времен года.

При наблюдении неба можно заметить, что звезды на протяжении многих лет неизменно сохраняют свое вза­имное расположение.

Звезды “неподвижны” лишь потому, что находятся очень далеко от нас. Расстояние до них так велико, что с любой точки земной орбиты они видны одинаково.

А вот тела же солнечной системы — Солнце, Луна и планеты, которые нахо­дятся сравнительно недалеко от Земли, и смену их положений мы можем легко заметить. Таким образом, Солнце наравне со всеми светила­ми участвует в суточном движении и одновременно имеет собст­венное видимое движение (оно называется годовым движением), обусловленное движением Земли вокруг Солнца.

Представьте себе картину — Луна взяла и исчезла с орбиты Земли. Чем нам может грозить такой поворот событий? Подробнее об этом

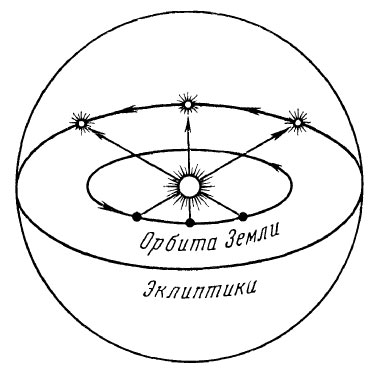
Видимое годовое движение Солнца на небесной сфере

Наиболее просто годовое движение Солнца можно объяснить по рисунку приведенному ниже. Из этого ри­сунка видно, что в зависимости от положения Земли на орбите наблюдатель с Земли будет видеть Солнце на фоне разных со­звездий. Ему будет казаться, что оно все время перемещается по небесной сфере. Это движение является отражением обращения Земли вокруг Солнца. За год Солнце сделает полный оборот.

Что представляет собой эклиптика

Большой круг на небесной сфере, по которому происходит ви­димое годовое движение Солнца, называется эклиптикой. Эклиптика — слово греческое и в переводе означает затмение. Этот круг назвали так потому, что затмения Солнца и Луны про­исходят только тогда, когда оба светила находятся на этом круге.

Следует отметить, что плоскость эклиптики совпадает с плос­костью орбиты Земли.

Видимое годовое движение Солнца по эк­липтике происходит в том же направлении, в котором Земля движется по орбите вокруг Солнца, т. е. оно перемещается к востоку. В течение года Солнце последовательно проходит по эк­липтике 12 созвездий, которые образуют пояс Зодиака и называются зодиакальными.

Пояс Зодиака образуют следующие созвездия: Рыбы, Овен, Телец, Близнецы, Рак, Лев, Дева, Весы, Скорпион, Стрелец, Ко­зерог и Водолей. Вследствие того, что плоскость земного экватора наклоне­на к плоскости орбиты Земли на 23°27 ‘ , плоскость небесного эк­ватора также наклонена к плоскости эклиптики на угол е=23°27′.

Наклон эклиптики к экватору не сохраняется постоян­ным (вследствие воздействия на Землю сил притяжения Солнца и Луны), поэтому в 1896 г. при утверждении астрономических постоянных ре­шено было наклон эклиптики к экватору считать усредненно равным 23°27’8″,26.

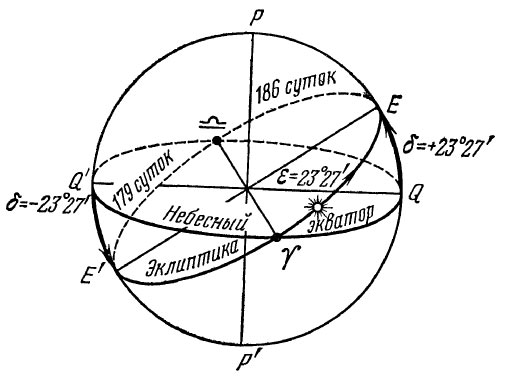
Небесный экватор и плоскость эклиптики

Эклиптика пересекается с небесным экватором в двух точках, которые называются точками весеннего и осеннего равноденствий. Точку весеннего равноденствия принято обозначать знаком созвездия Овен Т, а точку осеннего равноденствия — знаком созвездия Весов —. Солнце в этих точках соответственно бывает 21 марта и 23 сентября. В эти дни на Земле день равен ночи, Солнце точно восходит в точке восто­ка и заходит в точке запада.

Точки весеннего и осеннего равноденствия – места пересечения экватора и плоскости эклиптики

Точки эклиптики, отстоящие от точек равноденствий на 90°, называются точками солнцестояний. Точка Е на эклип­тике, в которой Солнце занимает самое высокое положение отно­сительно небесного экватора, называется точкой летнего солнцестояния, а точка Е’, в которой оно занимает самое низкое поло­жение, называется точкой зимнего солнцестояния.

В точке летне­го солнцестояния Солнце бывает 22 июня, а в точке зимнего солнцестояния — 22 декабря. В течение нескольких дней, близ­ких к датам солнцестояний, полуденная высота Солнца остается почти неизменной, в связи с чем эти точки и получили такое на­звание. Когда Солнце находится в точке летнего солнцестояния день в Северном полушарии самый длинный, а ночь самая корот­кая, а когда оно находится в точке зимнего солнцестояния — на­оборот.

В день летнего солнцестояния точки восхода и захода Солнца максимально удалены к северу от точек востока и запада на го­ризонте, а в день зимнего солнцестояния они имеют наибольшее удаление к югу.

Движение Солнца по эклиптике приводит к непрерывному из­менению его экваториальных координат, ежедневному изменению полуденной высоты и перемещению по горизонту точек восхода и захода.

Известно, что склонение Солнца отсчитывается от плоскости небесного экватора, а прямое восхождение — от точки весеннего равноденствия. Поэтому когда Солнце находится в точке весен­него равноденствия, его склонение и прямое восхождение равны нулю. В течение года склонение Солнца в настоящий период из­меняется от +23°26′ до —23°26′, переходя два раза в год через нуль, а прямое восхождение от 0 до 360°.

Солнце имеет форму шара или сплюснуто у полюсов? Давайте разберемся! Подробнее об этом

Экваториальные координаты Солнца в течение года

Экваториальные координаты Солнца в течение года изменя­ются неравномерно. Происходит это вследствие неравномерности движения Солнца по эклиптике и движения Солнца по эклиптике и наклона эклиптики к экватору. Половину своего видимого годо­вого пути Солнце проходит за 186 суток с 21 марта по 23 сентяб­ря, а вторую половину за 179 суток с 23 сентября по 21 марта.

Неравномерность движения Сол­нца по эклиптике связана с тем, что Земля на протяжении всего периода обращения вокруг Солнца движется по орбите не с оди­наковой скоростью. Солнце находится в одном из фокусов эллип­тической орбиты Земли.

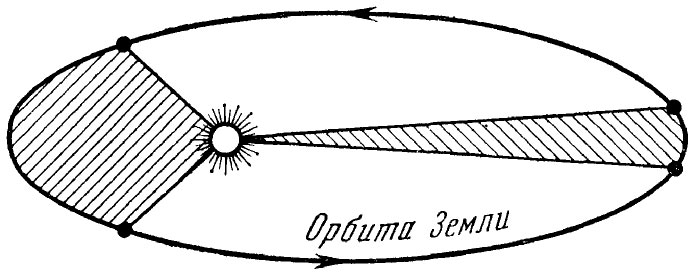
движение Земли по орбите

Из второго закона Кеплера известно, что линия, соединяющая Солнце и планету, за равные промежутки времени описывает равные площади. Согласно этому закону Земля, находясь ближе всего к Солнцу, т. е. в перигелии, движется быстрее, а находясь дальше всего от Солнца, т. е. в афелии — медленнее.

Ближе к Солнцу Земля бывает зимой, а летом — дальше. Поэтому в зим­ние дни она движется по орбите быстрее, чем в летние. Вследст­вие этого суточное изменение прямого восхождения Солнца в день зимнего солнцестояния равно 1°07′, тогда как в день летнего солнцестояния оно равно только 1°02′.

Различие скоростей движения Земли в каждой точке орбиты вызывает неравномерность изменения не только прямого восхож­дения, но и склонения Солнца. Однако за счет наклона эк­липтики к экватору его изменение имеет другой характер. Наиболее быстро склонение Солнца изменяется вблизи точек равноденствия, а у точек солнцестояния оно почти не из­меняется.

Знание характера изменения экваториальных координат Солн­ца позволяет производить приближенный расчет прямого восхож­дения и склонения Солнца.

Для выполнения такого расчета бе­рут ближайшую дату с известными экваториальными координа­тами Солнца. Затем учитывают, что прямое восхождение Солнца за сутки изменяется в среднем на 1°, а склонение Солнца в тече­ние месяца до и после прохождения точек равноденствия изме­няется на 0,4° в сутки; в течение месяца перед солнцестояниями и после них — на 0,1° в сутки, а в течение промежуточных меся­цев между указанными — на 0,3°.

Источник